Контрольная работа 1 АПз-310 / Электротехника Ч1

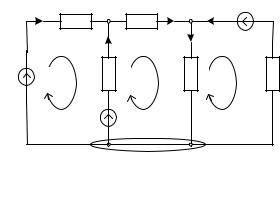
21

Схема рис. 2.1 содержит 5 ветвей (N=5), 3 cложных потенциальных узла (n = 3) и 3 независимых контура (к=3). Значит, в систему необходимо включить два уравнения по первому закону Кирхгофа (например, для уз- лов 1 и 2) и три уравнения по второму закону Кирхгофа (для контуров I, II, III).

Обозначим на схеме стрелками условно принятые положительные на- правления токов ветвей и направления обхода контуров. Будем полагать, что индексы токов ветвей совпадают с индексами пассивных приемников электрической энергии. Тогда система уравнений по законам Кирхгофа принимает вид:

Далее необходимо решить систему из пяти уравнений относительно токов. Точность расчетов может быть проверена с помощью уравнения ба- ланса мощностей источников и приемников электрической энергии:

22

В левой части уравнения слагаемые имеют знак плюс, если направления Э.Д.С. и токов совпадают. В противном случае они имеют знак минус.

2. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДОМ ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ

Когда в состав электрической цепи входит только один источник Э.Д.С., его ток определяется общим сопротивлением пассивных приемников электрической энергии. Такое сопротивление называют эквивалентным – Rэкв. Очевидно, что если известно Rэкв, то цепь можно представить в виде двух последовательно соединенных элементов – источника Э.Д.С. и Rэкв, а определение тока источника сводится к применению закона Ома. Процесс перехода от электрической цепи с произвольной топологией к цепи с Rэкв называется эквивалентным преобразованием. Такое преобразование и положено в основу рассматриваемого метода анализа.

Приемы преобразования электрической цепи определяются способами соединения пассивных элементов. Различают четыре основных способа со-

единения: последовательное, параллельное, треугольником и звездой. Рас-

смотрим сущность эквивалентных преобразований при каждом из названных способов.

2.1. Последовательное соединение элементов.

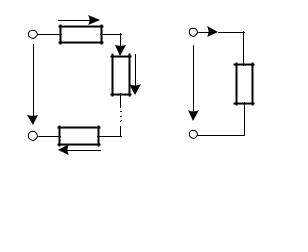
Электрическая схема с последовательным соединением элементов приведена на рис. 2.2, а. Такая цепь имеет только один контур. Через все элементы контура протекает один и тот же ток I. Согласно второму закону Кирхгофа, можно записать

R1 I + R2 I +…+ Rn I = Rэкв I,

23

откуда

а

I = U / Rэкв.

Таким образом, видим, что схема из n последовательно соединенных резистивных элементов может быть заменена схемой с одним элементом, сопротивление которого определяется по (2.1).

2.2. Параллельное соединение элементов.

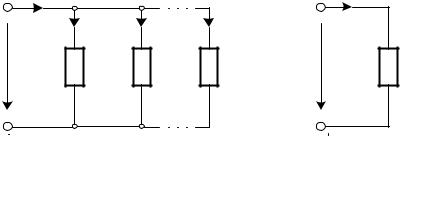
Параллельным называют соединение, при котором все элементы цепи присоединяются к двум сложным потенциальным узлам и находятся под воздействием одного и того же напряжения. Схема такой цепи приведена на рис. 2.3. Ток каждой к – ой ветви этой цепи определяется напряжением источника U и проводимостью Gк соответствующей ветви:

Определим правило эквивалентной замены разветвленной схемы рис.2.3, а на простейшую схему рис 2.3, б. Условием эквивалентности схем является равенство токов на зажимах 1 – 1′, т. е.:

Подставляя в (2.3) значение токов из (2.2), получим:

24

к=1

Таким образом, цепь, состоящая из n параллельных резистивных элементов, может быть заменена простейшей цепью, эквивалентное сопротивление которой определяется выражением (2.5).

При параллельном соединении двух резистивных элементов с сопротивлениями R1 и R2 их эквивалентное сопротивление равно:

Токи двух ветвей при их параллельном соединении определяются по правилу деления токов:

25

2.3.Соединение элементов звездой или треугольником.

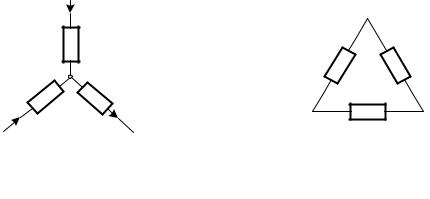
Соединение трех сопротивлений в виде трехлучевой звезды (рис. 2.4, а),

называют соединением «звезда», а соединение, при котором элементы об- разуют стороны треугольника (рис. 2.4, б), – «треугольник».

Очень часто при расчете электрических цепей оказывается целесообразным преобразовать треугольник в звезду. Полезность преобразования наглядно видна на примере схемы рис. 2.5. На рис. 2.5, а приведена схема до преобразования. Пунктиром обведен преобразуемый треугольник. На рис. 2.5, б приведена та же схема после преобразования. Расчет токов в ней значительно проще.

При преобразовании треугольника в звезду следует пользоваться выражениями:

26

2.4. Метод эквивалентных преобразований.

Суть метода:

1.Участки электрической цепи с последовательно и параллельно соединенными элементами заменяют одним эквивалентным элементом. Рядом последовательно выполненных преобразований схему упрощают до элементарного вида.

2.Применением закона Ома находится ток упрощенной схемы. Его значение определяет ток ветви, ближайшей к источнику Э.Д.С. (ток первой ветви). Это позволяет легко вычислить токи остальных ветвей.

Рассмотрим возможность применения метода на примере анализа схемы рис. 2.6, а. Будем полагать, что в схеме известны значение Э.Д.С. – Е и значения сопротивлений всех ветвей. Необходимо определить токи всех ветвей цепи.

Решение:

А) Выполняем ряд эквивалентных преобразований. Для этого:

1) Выделяем участок с параллельно соединенными сопротивлениями R4 и R5. Находим эквивалентное сопротивление этого участка:

R4,5 = R4 R5 .

R4 + R5

27

Приводим схему рис. 2.6, а к схеме рис. 2.6, б.

2) Находим эквивалентное сопротивление цепи относительно узлов а и б:

R= R2 (R3 + R4.5 ) . а,б R2 + R3 + R4,5

Теперь схема представляет контур с последовательно соединенными Е, R1 и Rа, б элементами (рис. 2.6, в), т. е. приведена к простейшему виду.

Б) Определяем токи ветвей. Для этого:

1) Находим ток простейшей схемы (ток первой ветви – I1):

I1 = Е / (R1 + Rа,б).

2) Возвращаемся к схеме рис. 2.6, б. Учитывая, что теперь в схеме известен ток I1, находим токи ветвей R2 и R3..Для этого достаточно применить правило деления токов (2.8):

Очевидно, что после определения тока I2, ток I3 легко вычислить и по первому закону Кирхгофа, т. е. I3 = I1 – I2.

3) Возвращаемся к схеме рис. 2.6, а. Так как теперь в схеме известны токи I1,I2 и I3, токи I4 и I5 находим по (2.8):

28

Таким образом, анализ электрической цепи рис. 2.6 проведен без со- ставления и решения системы из N = 5 линейных уравнений по законам Кирхгофа. В этом и заключается его основное достоинство.

3. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДОМ КОНТУРНЫХ ТОКОВ

Метод контурных токов оказывается полезным, когда схема электри- ческой цепи содержит несколько источников электрической энергии. Он по- зволяет выполнить анализ такой цепи решением системы из К канонических уравнений, где К равно числу независимых контуров.

Напомним, что канонические уравнения удобны для матричной фор- мы представления системы. В электротехнике матрицы применяют для со- кращенной записи системы уравнений и для упорядочения их решения.

Члены канонических уравнений снабжаются двумя индексами, при- чем первый индекс соответствует номеру строки, а второй – номеру столб- ца. Если ввести понятия контурных токов, контурных сопротивлений и Э.Д.С., а также взаимных сопротивлений, то формально записанное канони- ческое уравнение соответствует уравнению, составленному по второму за- кону Кирхгофа.

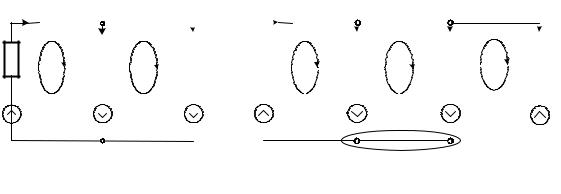
Рассмотрим метод на примере схемы, приведенной на рис. 2.7, а. Схе- ма имеет два независимых контура. Для ее анализа методом контурных то- ков необходимо составить систему из двух канонических уравнений:

29

где: I11, I22 – контурные токи, Е11, Е22 – контурные Э.Д.С., R11, R22 – кон- турные сопротивления, R12, R21 – взаимные сопротивления контуров.

Определим введенные понятия.

Под контурными токами понимают условные (расчетные) токи, замы-

кающиеся в соответствующих контурах. На рис 2.7, а направление кон-

турных токов показано стрелками в контурах. Пусть направление этих токов будет одинаковым – по часовой стрелке.

Сопоставляя контурные токи с токами ветвей, можно показать, что значение контурных токов совпадает со значением действительных токов только во внешних ветвях:

Токи смежных ветвей равны разности контурных токов соседних кон- туров:

I5 = I11 – I22.

Таким образом, по известным контурным токам легко найти действи- тельные токи всех ветвей. Следовательно, решение системы уравнений (2.10) относительно контурных токов отвечает целям анализа электрической цепи.

Для решения системы уравнений (2.10) определим понятия контурных

30

сопротивлений – R11, R22, контурных Э.Д.С. – Е11, Е22 и взаимных сопротив-

лений – R12, R21:

Теперь уравнения системы (2.10) полностью соответствуют парамет- рам схемы рис. 2.7, а. Значение взаимных сопротивлений контуров в (2.11) определено с обратным знаком. Это обусловлено необходимостью привести канонические уравнения (2.10) в соответствие с уравнениями, составленны- ми по второму закону Кирхгофа. Взаимное сопротивление контуров, не имеющих общих ветвей, равно нулю. Решая эту систему уравнений, можно найти контурные токи, а по ним искомые токи ветвей: I1, I2, I3, I4, I5.

Если бы схема содержала три контура, как на рис. 2.7, б, то система канонических уравнений имела бы вид:

R11 I11 + R12 I22 + R13 I33 = E11

R21 I11 + R22 I22 + R23 I33 = E22 .

R31 I11 + R32 I22 + R33 I33 = E33

Таким образом, метод контурных токов более экономен по вычисли- тельной работе. Он позволяет формализовать процесс анализа и упрощает применение ЭВМ к анализу сложных электрических цепей.

4. АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДОМ МЕЖДУУЗЛОВОГО НАПРЯЖЕНИЯ

В реальных электрических цепях часто источники и приемники элек- трической энергии включаются параллельно. Схемы таких цепей имеют только два узла. Если напряжение между узлами известно, то определение токов в ветвях цепи сводится к применению закона Ома. Этот факт и поло-