Контрольная работа 1 АПз-310 / Электротехника Ч1

51

3.10.Приведите соотношения между токами и напряжениями на R, L, и C элементах в комплексной показательной форме.

3.11.Каковы фазовые соотношения между током и напряжением на R, L и С эле-

ментах?

ЛЕКЦИЯ 4. КОМПЛЕКСНАЯ ФОРМА СОПРОТИВЛЕНИЯ И ПРОВОДИМОСТИ ЭЛЕМЕНТОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

1. КОМПЛЕКСНОЕ СОПРОТИВЛЕНИЕ

Введение комплексного представления токов и напряжений требует определить и сопротивление R, С и L элементов электрических цепей в комплексной форме – ZR, ZC и ZL.

Хорошо известно, что сопротивление резистора определяется как отношение напряжения на резисторе к току, протекающему через него. Если напряжение и ток представлены в комплексной форме, то

Но в предыдущей лекции было установлено, что на резистивном элементе напряжение и ток совпадают по фазе, т. е. ϕu = ϕi . Поэтому

Таким образом видим, что комплексное сопротивление резистора выражается только действительным числом. Оно не вносит фазовых искажений между током и напряжением. Чтобы подчеркнуть этот факт, такое сопротивление часто называют активным.

52

Комплексное сопротивление емкости определяется следующим отношением:

Видим, что комплексное сопротивление емкости переменному току выражается мнимым числом. Мнимая единица -j физически определяет сдвиг фаз между током и напряжением на 90о. Это хорошо согласуется с ее математическим значением:

−π

− j = e 2 .

Таким образом, напряжение на емкости отстает от тока на 90о. Это означает, что сначала растет ток, протекающий через конденсатор, затем, с некоторым отставанием увеличивается заряд и напряжение.

Коэффициент 1/ω C определяет величину сопротивления в Омах. Он обратно пропорционален частоте, называется емкостным сопротивлением и обозначается ХС, т.е.

Комплексное сопротивление индуктивности определяется отношени-

ем:

И в этом случае сопротивление выражается мнимым числом. Но так как это число положительное, это означает, что на индуктивности напряжение опережает ток на 90о.

Коэффициент ωL определяет величину сопротивления в Омах. Он пропорционален частоте, называется индуктивным сопротивлением и обозначается ХL, т.е.

53

Чтобы подчеркнуть тот факт, что сопротивления емкости и индуктивности выражаются мнимыми числами, их называют реактивными сопро-

тивлениями, а конденсатор и индуктивность – реактивными элементами

цепи.

Теперь определим комплексное сопротивление электрической цепи, содержащей активные и реактивные элементы, например, последовательно включенные R, L и С элементы (рис.4.1). Такая цепь представляет замкнутый контур, поэтому для нее справедлив второй закон Кирхгофа:

В последнем выражении проведем замену символов мгновенных напряжений и Э.Д.С. на их комплексные изображения по правилам, определенным в лекции 2. Такой прием получил название символического метода.

Так как ток, протекающий через все элементы последовательной цепи, одинаков, то (4.6) приходит к виду:

По определению выражение в правой части последнего равенства есть ни что иное, как комплексное сопротивление цепи рис.4.1, т.е.

X = (ωL − 1 ) – мнимая часть или реактивное сопротивление цепи.

ωC

54

Выражение (4.7) представляет комплексное сопротивление в алгебраической форме.

Соотношения между составляющими комплексного сопротивления находятся в полном соответствии с соотношениями для комплексного представления тока. Но для большей наглядности вводится понятие треугольни- ка сопротивления (рис.4.2). В треугольнике гипотенуза определяется модулем комплексного сопротивления Z, причем

Катет, прилежащий к острому углу ϕ Z определяет активное сопротив-

ление цепи R:

Противолежащий катет определяет реактивное сопротивление цепи Х:

Угол φZ определяет сдвиг фаз между током и напряжением, который вносится комплексным сопротивлением цепи:

Учитывая выражения (4.8) (4.11), легко перейти от алгебраической к тригонометрической форме комплексного сопротивления:

55

Применив формулу Эйлера, получим показательную комплексную форму представления сопротивления:

Теперь можно записать закон Ома для участка цепи без источника Э.Д.С. в комплексном изображении:

Выражение (4.14) показывает, что в цепях переменного тока модуль тока определяется отношением модуля напряжения (его амплитудного значения) к модулю комплексного сопротивления, а фаза тока определяется разностью фаз напряжения и комплексного сопротивления. Отсюда вытекает еще одно полезное для практики выражение:

2.КОМПЛЕКСНАЯ ПРОВОДИМОСТЬ

Вцепях постоянного тока проводимость резистора определяется отношением тока к напряжению:

G = UI = R1 .

Эта величина обратно пропорциональна сопротивлению. В цепях переменного тока следует пользоваться понятием комплексной проводимости, которая обозначается Y и, в общем случае, содержит действительную G и мнимую В части:

Y = G + jB.

Как и в цепях постоянного тока, комплексная проводимость участка цепи обратно пропорциональна комплексному сопротивлению, т.е.

56

где У - модуль комплексной проводимости.

Соотношение между составляющими комплексной формы представления проводимости аналогичны соотношениям между составляющими комплексного сопротивления. Комплексные проводимости элементов R, L и С обратно пропорциональны их комплексным сопротивлениям.

Комплексная проводимость резистора обратна его комплексному сопротивлению:

Комплексная проводимость конденсатора определяется законом Ома:

В заключение отметим, что комплексное сопротивление удобно применять для анализа участков электрической цепи с последовательным включением элементов, а комплексную проводимость – для анализа участков с параллельным включением элементов.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ

57

4.1.Что привело к необходимости ввести понятия комплексного сопротивления и комплексной проводимости R, L и С элементов электрической цепи?

4.2.Приведите соотношения, определяющие комплексное сопротивление R, L и С элементов. Сформулируйте физический смысл мнимой единицы j.

4.3.Приведите соотношения между составляющими комплексного сопротивле-

ния.

4.4.Сформулируйте закон Ома в комплексной форме.

4.5.Можно ли при анализе электрических цепей синусоидального тока воспользоваться методами, применяемыми в цепях постоянного тока?

4.6.В схеме рис. 4.1 известно: e(t) = 10 sin 314t, R = 10 Ом, L = 0,1 Гн, а С = 50,7·106Ф. Определите комплексное сопротивление цепи в алгебраической и показательной форме.

4.7.Используя данные п. 4.6 определите ток цепи рис. 4.1.

4.8.Используя данные п. 4.6 определите напряжение на R, L и С элементах цепи

рис. 4.1.

4.9.В каких случаях целесообразно применять комплексную проводимость R, L и

Сэлементов цепи?

4.10.Приведите соотношения, определяющие комплексную проводимость R, L и

Сэлементов.

ЛЕКЦИЯ 5. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭЛЕК-

ТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА

1. МГНОВЕННАЯ МОЩНОСТЬ ЦЕПИ С R, L И С ЭЛЕМЕНТАМИ

В общем случае мгновенная мощность определяется произведением тока на напряжение:

58

Определим мгновенную мощность для цепи с последовательно включенными R, L и С элементами (рис.4.1). Пусть в этой цепи протекает ток

Он одинаков для всех элементов цепи.

Напряжение цепи определяется суммой падений напряжений на отдельных элементах

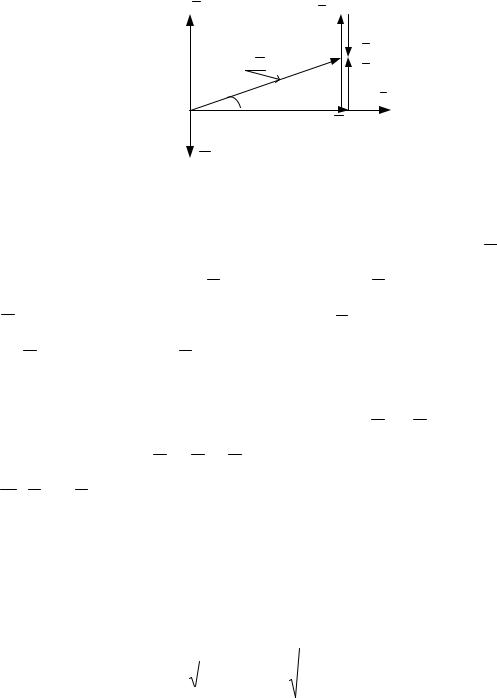
нию соответствует векторная диаграмма рис.5.1. В ней в качестве исходного принят вектор тока I . Вектор напряжения на индуктивности UL опережает ток, а вектор напряжения на емкости UC отстает от тока на 90о. Вектор на-

пряжения на резисторе Uа совпадает по фазе с током.

59

Рис. 5.1. Векторная диаграмма тока и напряжений в цепи с последовательным соединением R, L и С элементов

Проведем сложение векторов. Для этого начало вектора U L перемес-

тим в точку конца вектора Ua , а начало вектора UC - в точку конца вектора

U L . Результатом сложения является вектор U , выходящий из начала векто-

ра Ua в конец вектора UC . Угол ϕ определяет сдвиг фаз между током и результирующим напряжением, т. е. ϕ = ϕu − ϕi .

Соединим точки концов двух векторов – U и Ua . Обозначим вновь полученный вектор Ur = UL − UC . Образовавшийся треугольник из векторов

U; U a и U r называют треугольником напряжений. Для него справедливы следующие выражения:

60

Теперь возвратимся к формированию выражения для мгновенной мощности. Подставим (5.2) и (5.5) в (5.1). Тогда выражение для мгновенной мощности цепи рис. 4.1 примет вид:

Выражение (5.10) показывает, что мгновенная мощность цепи опреде-

ляется суммой слагаемых мощностей каждого из элементов. Оценка каж-

дого из слагаемых требует более детального анализа выражения (5.10).

2. АКТИВНАЯ, РЕАКТИВНАЯ, ПОЛНАЯ МОЩНОСТЬ

Для анализа (5.10) применим известные из курса тригонометрии формулы преобразования:

Как видно из (5.12), мгновенная мощность pR(t) содержит постоянную составляющую Р = RI2 и переменную, меняющуюся с удвоенной частотой. График рR(t) приведен на рис. 5.2. График наглядно показыва-

ет, что мощность рR(t) всегда положительна и изменяется от 0 (в мо-