19. Построение первоначальных опорных планов

Алгоритм симплекс-метода состоит из двух этапов

отыскания опорного решения

отыскание оптимального решения

Для получения начального опорного решения используются два способа

• метод Гаусса(метод последовательного исключения переменных)

• способ искусственного базиса или М-базиса.

19.1. Метод Гаусса

В канонической форме линейной задачи базисными переменными берут дополнительные переменные. Для получения базисного решения, все оставшиеся свободные переменные приравнивают к нулю. получается система n уравнений с n переменными. Данную систему можно решить методом Гаусса (метод исключения). Он состоит в следующем:

• Систему уравнения приводят к эквивалентной ей треугольной системе. Это называется прямым ходом.

• Из полученной треугольной системы переменные находят с помощью последовательных подстановок – обратный ход

При выполнении прямого хода используют следующие преобразования :

• Деление или умножение коэффициентов и свободных членов на одно и то же число

• Сложение и вычитание уравнений

• Перестановку уравнений системы

• Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю

Алгоритм отыскания решения системы n линейных уравнений методом Гаусса, с помощью ЭВМ, имеет следующие основные шаги:

1. Коэффициенты а_ij и свободные члены b_i системы размещаются в памяти ЭВМ в форме матрицы

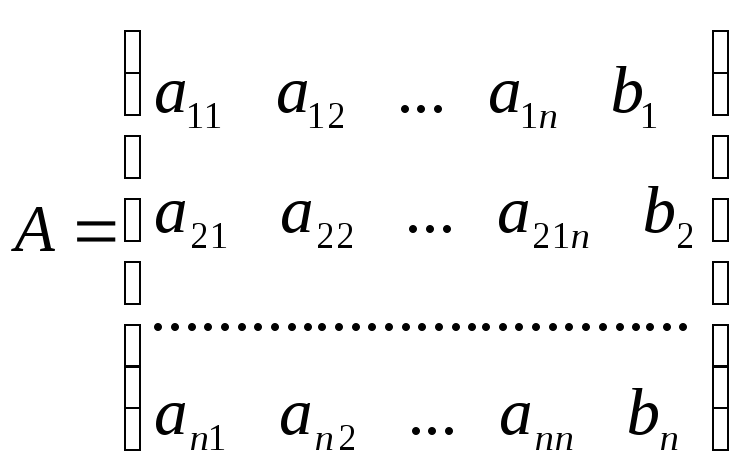
2. Ищем максимальный по модулю коэффициент в столбце.

3. Переставляем k-тую строку с первой строкой, содержащей максимальный коэффициент.

4. Преобразовываем все коэффициенты k–той строки путем деления на максимальный.

5. Преобразовываем с помощью k-той строки остальные строки k+1 - n.

6. Выполняем обратный ход Гаусса. Высчитываем значения переменных.

7. Построим опорный план, используя метод Гаусса.

Пример 1:

Решить систему линейных уравнений методом Гаусса.

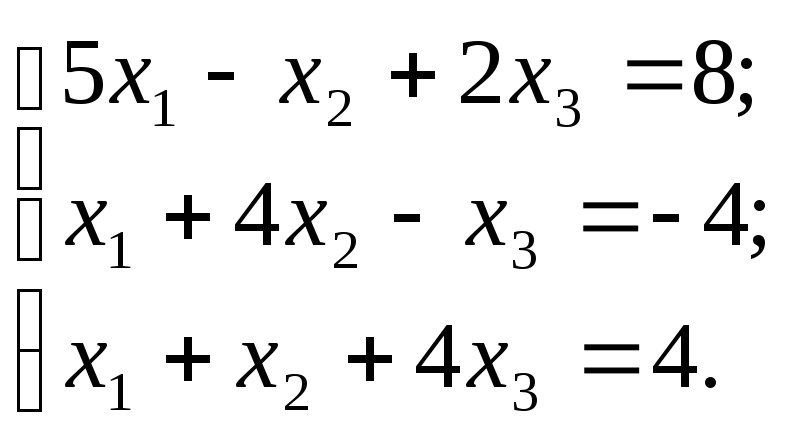(1)

Исключим, сначала неизвестное х₁ из 2-го и 3-го уравнения системы (1), используя первое уравнение.

Уравнение, с помощью которого преобразуют остальные уравнения называют разрешающим уравнением, а коэффициент этого уравнения при исключаемом неизвестном, называют разрешающим (главным) элементом.

В примере разрешающее уравнение первое, разрешающий элемент равен 5.

Разделим первое уравнение на 5 и вычтем из первого и третьего уравнений системы. Получим систему 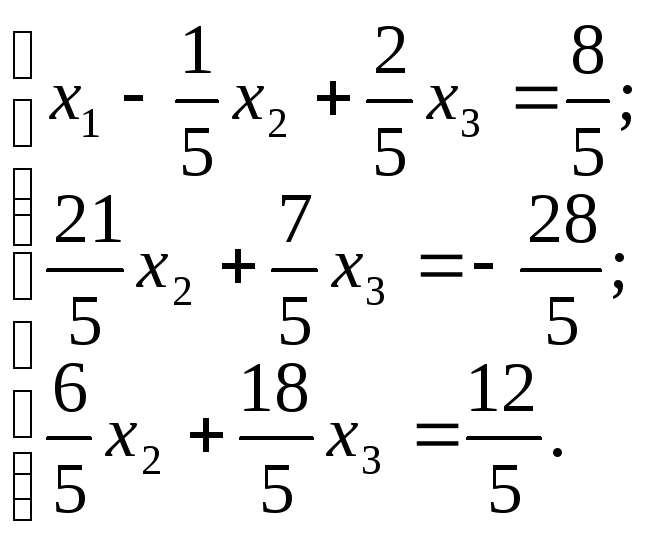(2)

(2)

Теперь второе уравнение будет разрешающим с разрешающим элементом (21/5). Разделим второе уравнение системы (2) на (21/5), получим второе уравнение. Умножим его на (6/5) и вычтем преобразованное второе уравнение из третьего. Получим систему 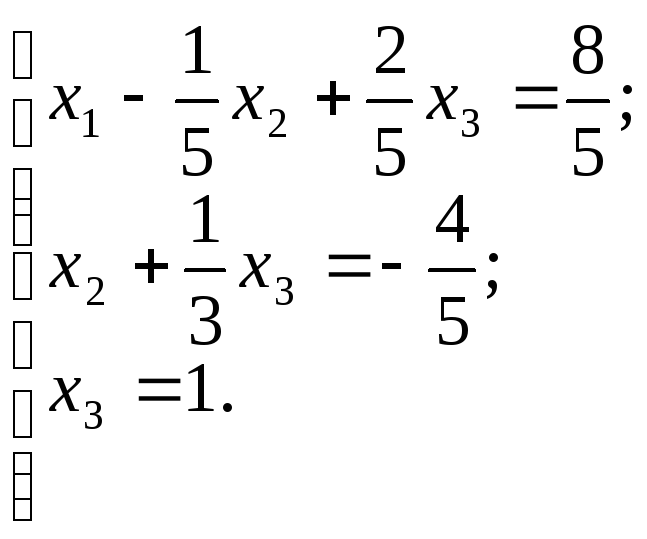(3):

(3)

Эти преобразования являются прямым ходом в методе Гаусса.

Умножим третье уравнение на (1/3) и вычтем его из второго. Затем третье уравнение умножим на (2/5) и вычтем его из первого. Получим систему (4):

(4)

Далее умножим второе уравнение системы (4) на (-1/5) и вычтем его из первого уравнения. Окончательно имеем систему 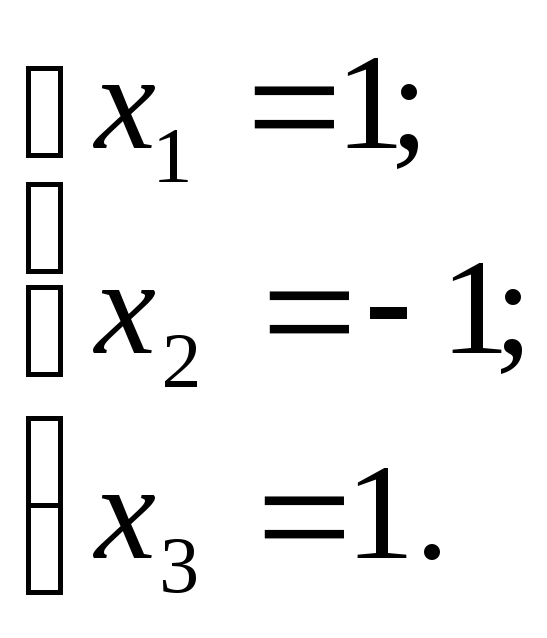(5):

(5)

Это и есть решения системы (1).

Пример 2

Коммерческое предприятие реализует три группы товаров (А, В, С). Плановые нормативы затрат ресурсов на 1т в рублях товарооборота, доход от продажи товаров на 1 т в рублях товарооборота, а так же объем ресурсов заданы. Определить плановый объем продаж и структуру товарооборота так, чтобы доход торгового предприятия был максимальным.

Таблица 1. Плановые нормативы затрат ресурсов.

Виды ресурсов	Нормы затрат на 1т в рублях товарооборота.			Объем ресурсов
	А	В	С
Рабочее время продавцов Площадь торговых залов Площадь складских помещений Доход	0,1 0,05 3 3	0,2 0,02 1 5	0,4 0,02 2 4	1100 120 8000 макс.

Запишем математическую модель:

х₁, х₂, х₃ - количество продаваемых товаров.

Доход (целевая функция) определяется:

При условии:

х₁ ≥ 0; х₂ ≥ 0; х₃ ≥ 0;

и ограничениях:

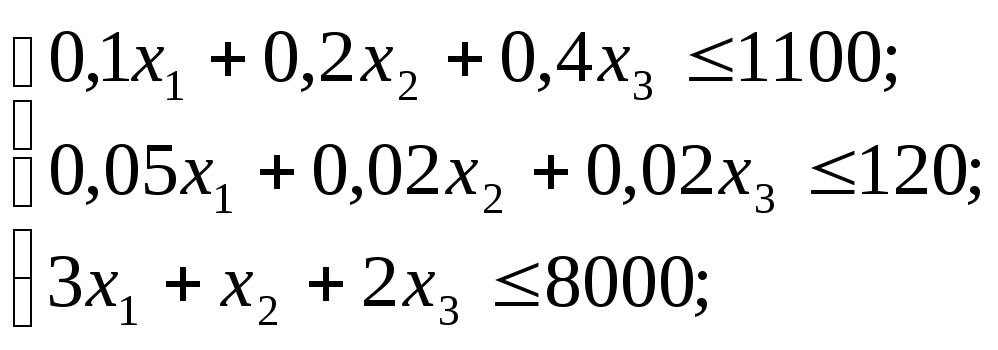
Для построения первого опорного плана приведем запись ОЗЛП в канонической форме:

При условии:

х₁ ≥ 0; х₂ ≥ 0; х₃ ≥ 0;

и ограничениях

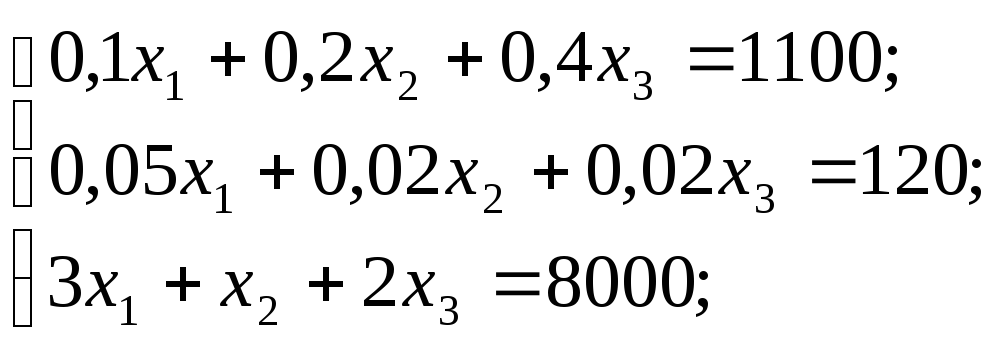
Запишем математическую модель в векторном виде:

где С = (3 5 4 0 0 0 ) – вектор-строка из коэффициентов целевой функции

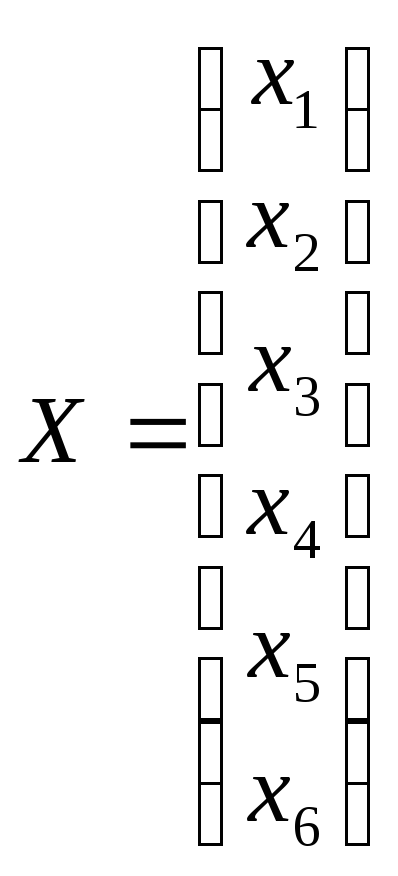- вектор-столбец переменных

при условии: вектор Х ≥ 0

и ограничениях:

где матрица:

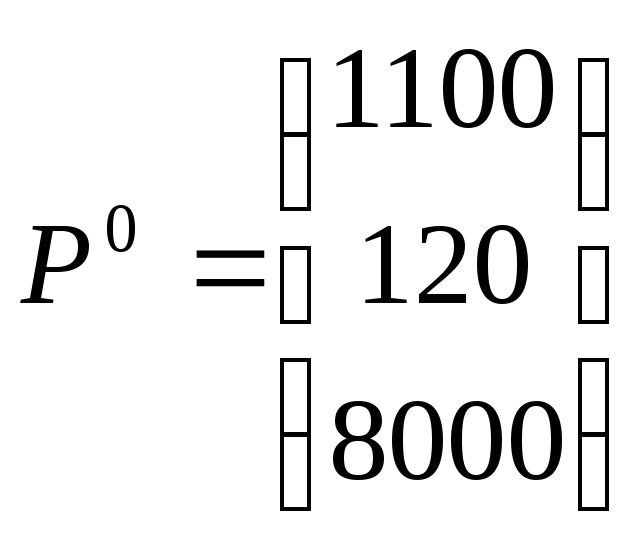
Находим первый опорный план.

Базисные переменные: х₄; х₅; х₆.

Свободные переменные: х₁=0; х₂=0; х₃=0;

В этом случае значения базисных переменных равны значениям свободных членов. Построим таблицу:

Коэффициенты целевой функции			3	5	4	0	0	0
План	Базисные переменные	Значения базисных переменных	х1	х2	х3	х4	х5	х6	zi
1	х4 x5 x6	1100 120 8000	0,1 0,05 3	0,2 0,02 1	0,4 0,02 2	1 0 0	0 1 0	0 0 1
Индексная строка	F(X)	0	- 3	- 5	-4	0	0	0