
ГОС / 33
.doc33. Геометрическая оптика, как предельный случай волновой. Зеркала, линзы, призмы, оптические приборы.
Луч
– это прямая или кривая линия, вдоль
которой распространяется энергия
светового поля (распространяется фронт
волны). Таким образом, геометрическая
оптика описывает распространение
электромагнитного поля как распространение
лучей в пространстве. Т.е. геометрическая
оптика есть волновая в приближении
коротких волн (![]() ).
).
Пусть пучок лучей
от точечного источника падает на плоское
зеркало. Рассмотрев два луча падающих
на плоское зеркало под разными углами,
получим, что каждый из этих лучей
отразится от зеркала по закону отражения,
и угол каждого из них с нормалью останется
после отражения неизменным. Так л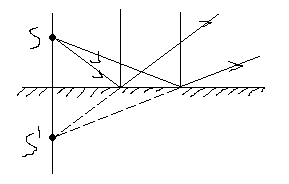 учи
произвольно взяты, то можно утверждать,
что при отражении от плоского зеркала
пучок световых лучей, исходящих из одной
точки, превращается в световой пучок,
в котором продолжения всех световых
лучей снова пересекаются в одной и той
же точке (штриховая линия). В результате
наблюдателю, помещенному на пути
отраженных лучей, они будут казаться
пересекающимися в точке
учи
произвольно взяты, то можно утверждать,
что при отражении от плоского зеркала
пучок световых лучей, исходящих из одной
точки, превращается в световой пучок,
в котором продолжения всех световых
лучей снова пересекаются в одной и той
же точке (штриховая линия). В результате
наблюдателю, помещенному на пути
отраженных лучей, они будут казаться
пересекающимися в точке
![]() ,
и эта точка будет мнимым изображением
точки
,
и эта точка будет мнимым изображением
точки
![]() .
Для протяженного объекта каждая его
точка изобразиться в плоском зеркале
также в виде точки, следовательно, мнимое
изображение так же будет протяженный
объект тех же размеров, что и источник.
.
Для протяженного объекта каждая его
точка изобразиться в плоском зеркале
также в виде точки, следовательно, мнимое
изображение так же будет протяженный
объект тех же размеров, что и источник.
Рассмотрим
сферическое зеркало. 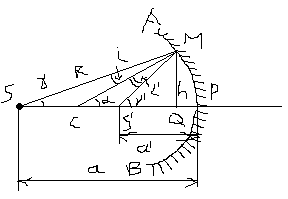 На
рис. изображено сечение АРВ
вогнутого сферического зеркала радиуса
На
рис. изображено сечение АРВ
вогнутого сферического зеркала радиуса
![]() ;
;
![]() – центр сферы. Средняя точка имеющейся
части сферической поверхности называется
полюсом
зеркала Р.
Нормаль к зеркалу, проходящая через
центр зеркала и через его полюс, называется
главной
оптической осью
зеркала. Нормали к зеркалу, проведенные
в других точках ее поверхности и также
проходящие через центр зеркала
– центр сферы. Средняя точка имеющейся
части сферической поверхности называется
полюсом
зеркала Р.
Нормаль к зеркалу, проходящая через
центр зеркала и через его полюс, называется
главной
оптической осью
зеркала. Нормали к зеркалу, проведенные
в других точках ее поверхности и также
проходящие через центр зеркала
![]() ,
носят название побочных
оптических
осей (ось МС).
Диаметр окружности, ограничивающей
сферическое зеркало, носит название
отверстия
зеркала.
Пусть точечный источник света
,
носят название побочных
оптических
осей (ось МС).
Диаметр окружности, ограничивающей
сферическое зеркало, носит название
отверстия
зеркала.
Пусть точечный источник света
![]() расположен на главной оси зеркала на
расстоянии
расположен на главной оси зеркала на
расстоянии
![]() от полюса. Рассмотрим луч
от полюса. Рассмотрим луч
![]() ,
принадлежащий к узкому пучку, т.е.
образует с осью малый угол
,
принадлежащий к узкому пучку, т.е.
образует с осью малый угол
![]() и падающий на зеркало в точке М
на высоте
и падающий на зеркало в точке М
на высоте
![]() над осью, так что
над осью, так что
![]() мало по сравнению с
мало по сравнению с
![]() и с радиусом зеркала
и с радиусом зеркала
![]() .
Отраженный луч пересечет ось в точке
.
Отраженный луч пересечет ось в точке
![]() на расстоянии
на расстоянии
![]() от полюса. Угол, образуемый отраженным
лучом с осью, обозначим
от полюса. Угол, образуемый отраженным
лучом с осью, обозначим
![]() .
Он также будет мал. СМ
есть перпендикуляр к поверхности зеркала
в точке падения,
.
Он также будет мал. СМ
есть перпендикуляр к поверхности зеркала
в точке падения,
![]() - угол падения,
- угол падения,
![]() - угол отражения. По закону отражения
- угол отражения. По закону отражения
![]() .
Обозначим буквой
.
Обозначим буквой
![]() угол, образуемый радиусом СМ
с осью. Из треугольника
угол, образуемый радиусом СМ
с осью. Из треугольника
![]() имеем
имеем
![]() ,
а из треугольника
,
а из треугольника
![]()
![]() ,
тогда
,
тогда
![]() (*). Так как рассматривается узкий пучок
лучей, прилегающий к главной оси (углы
малы), то можно заменить синусы углов
самими углами и пренебречь длиной
отрезка
(*). Так как рассматривается узкий пучок
лучей, прилегающий к главной оси (углы
малы), то можно заменить синусы углов
самими углами и пренебречь длиной
отрезка
![]() .
Тогда имеем приближенные равенства:
.
Тогда имеем приближенные равенства:
![]() ,
,
![]() ,
,
![]() .
Подставляя в (*) и сокращая на общий
множитель
.
Подставляя в (*) и сокращая на общий
множитель
![]() ,
находим основную формулу сферического
зеркала:
,
находим основную формулу сферического
зеркала:
![]() .
В сферическом зеркале при отражении
изображение точечного источника является
снова точка.
.
В сферическом зеркале при отражении
изображение точечного источника является
снова точка.
П ри
построении изображения любого источника
нет надобности рассматривать много
лучей. Для этого достаточно построить
два луча; точка их пересечения определит
местоположение изображения. Удобнее
всего построить те лучи, ход которых
легко проследить. Ход этих лучей в случае
отражения от зеркала изображен на
рисунке. Луч 1 проходит через центр
зеркала и поэтому нормален к поверхности
зеркала. Этот луч возвращается после
отражения точно назад вдоль побочной
или главной оптической оси. Луч 2
параллелен главной оптической оси
зеркала. Этот луч после отражения
проходит через фокус зеркала. Луч 3,
который от точки объекта проходит через
фокус зеркала. После отражения от зеркала
он идет параллельно главной оптической
оси. Луч 4, падающий на зеркало в его
полюсе, отразиться назад симметрично
по отношению к главной оптической оси.
Для построения изображения можно
воспользоваться любой парой этих лучей.
Построив изображения достаточного
числа точек протяженно объекта, можно
составить представление о положении
всего объекта. В случае простой формы,
достаточно построить всего одну точку
изображения
ри
построении изображения любого источника
нет надобности рассматривать много
лучей. Для этого достаточно построить
два луча; точка их пересечения определит
местоположение изображения. Удобнее
всего построить те лучи, ход которых
легко проследить. Ход этих лучей в случае
отражения от зеркала изображен на
рисунке. Луч 1 проходит через центр
зеркала и поэтому нормален к поверхности
зеркала. Этот луч возвращается после
отражения точно назад вдоль побочной
или главной оптической оси. Луч 2
параллелен главной оптической оси
зеркала. Этот луч после отражения
проходит через фокус зеркала. Луч 3,
который от точки объекта проходит через
фокус зеркала. После отражения от зеркала
он идет параллельно главной оптической
оси. Луч 4, падающий на зеркало в его
полюсе, отразиться назад симметрично
по отношению к главной оптической оси.
Для построения изображения можно
воспользоваться любой парой этих лучей.
Построив изображения достаточного
числа точек протяженно объекта, можно
составить представление о положении
всего объекта. В случае простой формы,
достаточно построить всего одну точку
изображения
![]() .
.
Л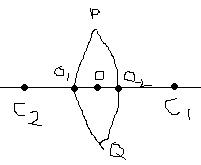 инза
представляет собой прозрачное вещество,
ограниченное с двух сторон сферическими
поверхностями; в частном случае одна
из поверхностей линзы может быть
плоскостью, которую можно рассматривать
как сферическую поверхность бесконечно
большого радиуса. Рассмотрим линзу,
ограниченную двумя сферическими
преломляющими поверхностями
инза
представляет собой прозрачное вещество,
ограниченное с двух сторон сферическими
поверхностями; в частном случае одна
из поверхностей линзы может быть
плоскостью, которую можно рассматривать
как сферическую поверхность бесконечно
большого радиуса. Рассмотрим линзу,
ограниченную двумя сферическими
преломляющими поверхностями
![]() и
и
![]() .
Центр первой преломляющей поверхности
.
Центр первой преломляющей поверхности
![]() лежит в точке
лежит в точке
![]() ,
центр второй
,
центр второй
![]() –
–
![]() .
Точка
.
Точка
![]() называется оптическим
центром
линзы. Всяка прямая, проходящая через
оптический центр, называется оптической
осью линзы.
Та из осей, которая проходит через центры
обеих преломляющих поверхностей линзы,
называется главной,
остальные – побочными.
Луч, идущий по какой-либо из оптических
осей, проходя через линзу, практически
не меняет своего направления. Если на
линзу падает световой луч не вдоль одной
из ее оптических осей, а по какому-либо
другому направлению, то он, испытав
преломление сначала на первой
ограничивающей линзу поверхности, потом
на второй, отклониться от первоначального
направления. Если в некоторой точке на
главной оси за линзой расположить экран
и на ней будет видна яркая точка, то эта
точка на главной оптической оси называется
главным фокусом (точка, где пересекаются
после преломления в линзе лучи), а
расстояние от оптического центра до
главного фокуса называется фокусным
расстоянием линзы. Для тонких линз
справедливо равенство
называется оптическим
центром
линзы. Всяка прямая, проходящая через
оптический центр, называется оптической
осью линзы.
Та из осей, которая проходит через центры
обеих преломляющих поверхностей линзы,
называется главной,
остальные – побочными.
Луч, идущий по какой-либо из оптических
осей, проходя через линзу, практически
не меняет своего направления. Если на
линзу падает световой луч не вдоль одной
из ее оптических осей, а по какому-либо
другому направлению, то он, испытав
преломление сначала на первой
ограничивающей линзу поверхности, потом
на второй, отклониться от первоначального
направления. Если в некоторой точке на
главной оси за линзой расположить экран
и на ней будет видна яркая точка, то эта
точка на главной оптической оси называется
главным фокусом (точка, где пересекаются
после преломления в линзе лучи), а
расстояние от оптического центра до
главного фокуса называется фокусным
расстоянием линзы. Для тонких линз
справедливо равенство
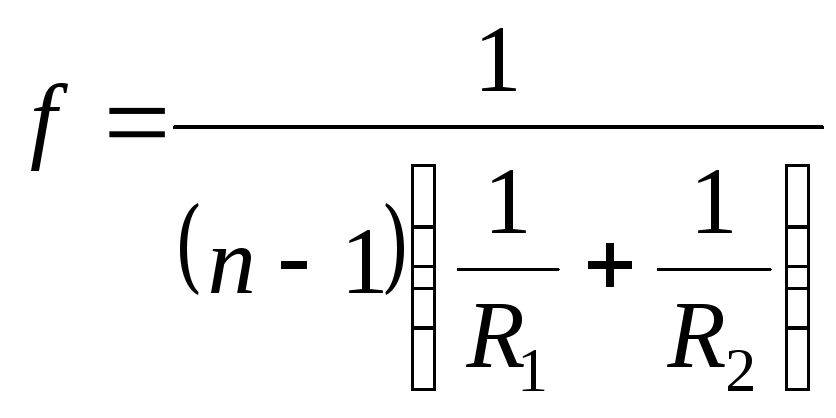 ,
где
,
где
![]() - показатель преломления вещества, из
которого сделана линза,
- показатель преломления вещества, из
которого сделана линза,
![]() и
и
![]() - радиусы сферических поверхностей
линзы,
- радиусы сферических поверхностей
линзы,
![]() - фокусное расстояние линзы. Для
характеристики оптических свойств
различных линз часто пользуются
величиной, обратной фокусному расстоянию
линзы – оптическая сила линзы (
- фокусное расстояние линзы. Для
характеристики оптических свойств
различных линз часто пользуются
величиной, обратной фокусному расстоянию
линзы – оптическая сила линзы (![]() )
)
![]() .
Чем короче фокусное расстояние, те
сильнее преломляет линза и тем больше
.
Чем короче фокусное расстояние, те
сильнее преломляет линза и тем больше
![]() .
.
![]() - оптическая сила линзы, фокусное
расстояние которой равно 1 м.
Существуют собирающие линзы и рассеивающие.
- оптическая сила линзы, фокусное
расстояние которой равно 1 м.
Существуют собирающие линзы и рассеивающие.
Д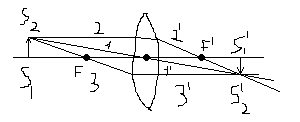 ля
построения изображения в линзе любой
точки объекта, так же как и при построении
изображения в зеркале, достаточно найти
точку пересечения каких-либо двух лучей,
исходящих из этой точки. Наиболее простое
построение выполняется при помощи лучей
указанных на рисунке. Луч 1 идет вдоль
побочной оси без изменения направления.
Луч 2 падает на линзу параллельно главной
оси; преломляясь, этот луч проходит
через задний фокус
ля
построения изображения в линзе любой
точки объекта, так же как и при построении
изображения в зеркале, достаточно найти
точку пересечения каких-либо двух лучей,
исходящих из этой точки. Наиболее простое
построение выполняется при помощи лучей
указанных на рисунке. Луч 1 идет вдоль
побочной оси без изменения направления.
Луч 2 падает на линзу параллельно главной
оси; преломляясь, этот луч проходит
через задний фокус
![]() .
Луч 3 проходит через передний фокус
.
Луч 3 проходит через передний фокус
![]() ;
преломляясь, этот луч идет параллельно
главной оптической оси.
;
преломляясь, этот луч идет параллельно
главной оптической оси.
![]()
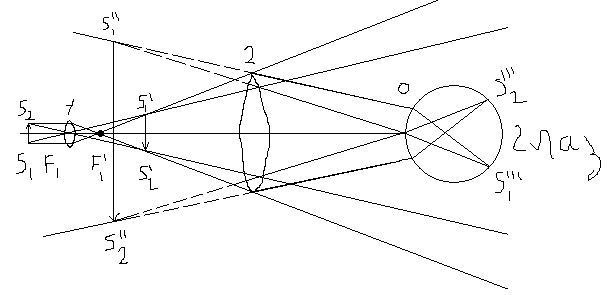 -оптика
была разработана в 70-х годах 20 века.
Линзы представляли собой цилиндр с
переменным показателем преломления
вдоль радиуса этого цилиндра. Лучи
преломлялись в разных точках этого
цилиндра по-разному и сходились в одной
точке образуя изображение. Оптическая
система микроскопа состоит из двух и
более частей или менее сложной конструкции:
объектива и окуляра. Ход лучей в микроскопе
показан на рисунке, причем объектив и
окуляр заменены на рисунке простыми
линзами. Микроскоп дает возможность
рассматривать изображение предмета
под большим углом, чем это возможно для
невооруженного глаза. Увеличением
микроскопа, называется отношение длины
изображения какого-либо отрезка,
поучаемого на сетчатой оболочке глаза
при помощи микроскопа, к длине изображения
того же отрезка на сетчатке при
рассматривании его невооруженным
глазом. Увеличение микроскопа значительно
больше увеличения, даваемого объективом
или окуляром. Исключительное значение
имеют телескопы в астрономии. Современные
телескопы имеют огромные размеры и
представляют собой весьма сложные
сооружения. Телескоп представляет собой
оптический прибор, предназначенный для
рассматривания глазом весьма удаленных
предметов. Как и микроскоп он состоит
из объектива и окуляра; и тот и другой
являются более или менее сложными
оптическими системами, хотя и не столь
сложными, как в случае микроскопа. В
телескопах объектив и окуляр располагаются
так, что задний фокус объектива почти
совпадает с передним фокусом окуляра.
Объектив дает действительное уменьшенное
обратное изображение бесконечно
удаленного предмета в своей задней
фокальной плоскости; это изображение
рассматривается в окуляр, как в лупу.
Наряду с телескопами, построенными по
типу зрительной трубы – рефракторами,
весьма важное значение в астрономии
имеют зеркальные (отражательные)
телескопы, или рефлекторы.
-оптика
была разработана в 70-х годах 20 века.
Линзы представляли собой цилиндр с
переменным показателем преломления
вдоль радиуса этого цилиндра. Лучи
преломлялись в разных точках этого
цилиндра по-разному и сходились в одной
точке образуя изображение. Оптическая
система микроскопа состоит из двух и
более частей или менее сложной конструкции:
объектива и окуляра. Ход лучей в микроскопе
показан на рисунке, причем объектив и
окуляр заменены на рисунке простыми
линзами. Микроскоп дает возможность
рассматривать изображение предмета
под большим углом, чем это возможно для
невооруженного глаза. Увеличением
микроскопа, называется отношение длины
изображения какого-либо отрезка,
поучаемого на сетчатой оболочке глаза
при помощи микроскопа, к длине изображения
того же отрезка на сетчатке при
рассматривании его невооруженным
глазом. Увеличение микроскопа значительно
больше увеличения, даваемого объективом
или окуляром. Исключительное значение
имеют телескопы в астрономии. Современные
телескопы имеют огромные размеры и
представляют собой весьма сложные
сооружения. Телескоп представляет собой
оптический прибор, предназначенный для
рассматривания глазом весьма удаленных
предметов. Как и микроскоп он состоит
из объектива и окуляра; и тот и другой
являются более или менее сложными
оптическими системами, хотя и не столь
сложными, как в случае микроскопа. В
телескопах объектив и окуляр располагаются
так, что задний фокус объектива почти
совпадает с передним фокусом окуляра.
Объектив дает действительное уменьшенное
обратное изображение бесконечно
удаленного предмета в своей задней
фокальной плоскости; это изображение
рассматривается в окуляр, как в лупу.
Наряду с телескопами, построенными по
типу зрительной трубы – рефракторами,
весьма важное значение в астрономии
имеют зеркальные (отражательные)
телескопы, или рефлекторы.
