
ГОС / 36
.doc36. Оптко-механическая аналогия.
Механика частиц и геометрическая оптика очень схожи по своей структуре.
Механика |
Оптика |
|
Траектория. |
Луч. |
|
Скорость материальной точки. |
Групповая скорость. |
|
Полная энергия E. |
Частота . |
|
Потенциальная энергия U. |
Показатель преломления n. |
Аналогия существует не только между понятиями, но и между законами.
В механике известен принцип наименьшего действия.
![]() (5.1)
(5.1)
p – импульс.
Движение осуществляется по траектории, физическая величина действия для которой минимальна.
В оптике существует принцип Ферма.
![]() -
min.
(5.2)
-
min.
(5.2)
Оптическая длина пути минимальна.
![]() (5.3)
(5.3)
Т – период.
сТ – const.
![]() - min. (5.2)
- min. (5.2)
Если
Р~1/, то выражения
5.1 и 5.2 аналитически одинаковы. Аналогия
между оптическими и механическими
явлениями навела де Бройля на мысль
приписать частицам волновые свойства.
Де Бройль считал, что частица это реальная
волна или группа волн, распределённая
в пространстве. Взяв коэффициент
пропорциональности 2![]() ,
он получил соотношение де Бройля.
,
он получил соотношение де Бройля.
![]() (5.4)
(5.4)
![]() (5.4¢)
(5.4¢)
Получим основные уравнения квантовой теории света.
1.
![]() ,
,
![]()
![]() - энергия кванта.
- энергия кванта.
2.
![]() ,
,
![]()
![]()
Первоначально Планк приписал световым квантам свойства частиц, а де Бройль наоборот, предложил приписать частицам волновые свойства.
С движением всякой свободной частицы с энергией E и импульсом p, он связывал плоскую монохроматическую волну.
![]() (5.5)
(5.5)
w - частота, t
– время,
![]() - фаза волны.
- фаза волны.
![]() – волновой вектор, показывающий
направление распространения волны.
– волновой вектор, показывающий
направление распространения волны.
![]() – радиус вектор, характеризующий
положение любой точки волны.
– радиус вектор, характеризующий
положение любой точки волны.
![]() (5.6)
(5.6)
Из уравнений 5.7 и 5.7¢ видно, что координата точки волны с течением времени перемещается в пространстве по линейному закону со скоростью, которую можно получить, продифференцировав 5.7¢ по времени. Эту скорость мы будем обозначать U и называть фазовой скоростью.
![]() (5.8)
(5.8)
![]() (5.9)
(5.9)
Скорость, с которой распространяются все точки волны с одинаковой фазой, называется фазовой. Если фазовая скорость зависит от волнового вектора, в этом случае говорят, что имеет место дисперсия волны (вообще зависимость частоты от волнового вектора называется законом дисперсии).
Опыты Девиссона-Джермера.
Опыты были проделаны в 1927 году. Они изучали рассеяние пучка электронов на поверхности кристаллов. Они направляли пучок электронов с энергиями от 40 до 300 эВ нормально на монокристалл. Монокристалл брался достаточно больших размеров, чтобы электроны не попадали внутрь его. При этом поверхность полировалась так, что практически представляла одномерную дифракционную решетку. Они наблюдали рассеяние пучка электронов по углом φ с помощью устройства «цилиндр Фарадея», который шел к гальванометру. По силе тока можно судить о количестве электронов, рассеянных монокристаллом.
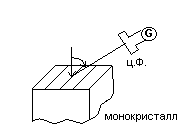
Т.к. поверхность монокристалла представляет дифракционную решетку, то условия главных максимумов запишется так:
![]() (6.1)
(6.1)
![]() (6.2),
(6.2),
где d – постоянная решетки. Она равна расстоянию между атомами;
φ – угол рассеяния.
Считая, что электроны испытывают дифракцию, можно определить из этого соотношения волну де Бройля.
В
этом эксперименте задавалась энергия
электронов, а определялся угол рассеяния
или дифракция.
![]()
![]() (6.3)
(6.3)
![]() -
что и наблюдалось в опыте.
-
что и наблюдалось в опыте.
Наблюдая за интенсивностью пучков электронов в зависимости от φ они заметили, что распределение электронов по углам весьма сходно с интенсивностью распределения волн при дифракции. Эти опыты привели к заключению о справедливости гипотезы де Бройля, в частности, формулы (6.2).
Опыты Тартаковского-Томсона: В 1927 году были проведены опыты Тартаковского-Томсона по дифракции электрона. Они применили метод де Бая - Шерера для дифракции рентгеновского излучения для электронов с заданными импульсами, которые падали на порожек из некоторого поликристаллического вещества. Данный образец брался очень тонким (порядка 10-5см), чтобы электроны могли проникать внутрь поликристалла, испытывая при этом объемную дифракцию.
Электроны падали на образец под углом скольжения θ, при этом наблюдались концентрические окружности с центром, который получался при проектировании основного пучка электронов на экран.
P
q d{ q Ф Д
Образец содержит большое число монокристаллов, ориентированных хаотически. Пусть некоторый монокристалл имеет плоскость, параллельную плоскости образца. Тогда для него выполняется условие Вульфа – Брега, которое является условием максимума для объемной дифракции. θ – угол скольжения, а d – расстояние между атомными плоскостями, являющимися постоянным для объемной пространственной решетки. На экране появляется максимум в точке P. Если другой монокристалл ориентирован под тем же углом к оси пучка, но отличается от угла θ поворотом оси, он тоже имеет максимум, но в другой точке, например, в Ф и т.д. Совокупность точек, а именно дифракционные максимумы образуют кольца на экране симметрично оси пучка. Определяя диаметры колец, а значит расстояние до образца, определяем θ, а зная d, можно определить длину волны.
При
этом задавалась разгоняющая разность
потенциалов. Используя формулу де
Бройля, можно получить:
![]() (6.4),
(6.4),
![]() ,
где Д – диаметр кольца.
,
где Д – диаметр кольца.
Тартаковский и Томсон получили соотношение, тем самым доказав выражение (6.2) для волны де Бройля.
Из этих экспериментов можно сделать вывод, что эти опыты подтвердили гипотезу де Бройля о волновой природе частиц, при этом реальность дифракции частиц уже не вызывали сомнения, однако интерпретация частиц, как некоторых образцов из волн являлось неверным. Там, при дифракции микрочастиц имеет место расширение первоначального пучка на дифракционные пучки, движущиеся в направлении главных максимумов. При уменьшении интенсивности первоначального пучка дифракционная картина сохраняется, но на месте сплошных колец наблюдаются отдельные вспышки (как для частиц, так и для волн). И если первоначальную волну отождествлять с размазанным веществом, то дифракционные пучки – это части частицы. Т.е. при дифракции вещество одной и той же частицы должно концентрироваться в разных местах экрана, что является неверным, т.к. вспышку на экране дает целый электрон, а не его часть. Опыты по дифракции микрочастиц не дает основания считать, что вещество частицы распределено в пространстве в соответствии с амплитудами волны де Бройля. При изменении интенсивности падающего пучка на экране наблюдаются отдельные вспышки, что наблюдалось как для частиц, так и для волн. Другая интерпретация опытов по дифракции состоит в том, что волна де Бройля имеет вероятностную природу. Максимум амплитуды волны де Бройля совпадает с максимумом вероятности обнаружить частицу в данном месте, а совокупность дифракционных максимумов – это совокупность максимумов вероятности обнаружения частицы, имеющей определенный импульс и энергию. Вероятность обнаружить частицу для любой области одинакового объема одинакова, т.е. точно задавая импульс частицы, приходим к полной неопределенности координаты и наоборот. Волновая функция.
