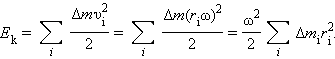ГОС / 3

Вращение твердого тела относительно неподвижной оси.

Абсолютно твердое тело – это тело деформацией, которого можно пренебречь. Вращательным называется такое движение, при котором 2 точки принадлежащие телу остаются все время неподвижными при движении. Прямая проходящая через 2 точки называется осью вращения. Основными параметрами движения является:

1. Угол поворота (угловое перемещение) является величиной векторной, определяется по правилу Буравчика.2. Угловая скорость = направлена по оси.3. Угловое ускорение

поступательное	вращательное
S
V
a
Рисунок1. Вращение диска относительно оси, проходящей через его центр O.

Связь линейного и углового перемещения S=r

Отсюда следует связь между модулями линейной и угловой скоростей:

υ = rω,

и между модулями линейного и углового ускорения:

a = aτ = rε.

Векторы и направлены по касательной к окружности радиуса r. Следует вспомнить, что при движении тела по окружности возникает также нормальное или центростремительное ускорение, модуль которого есть

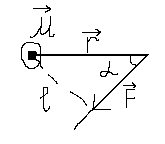
1.Моментом силы F относительно произвольной точки называется векторное произведение радиус вектора на силу.

M= rF M= r*F*sin (r F) r*sin=l М= l*F l- кратчайшее расстояние от точки наблюдения до линии, вдоль которой действует сила (плечо силы).

2.Моментом импульса (L) материальной точки называется векторная величина равная произведению радиус вектора на импульс материальной точки.

L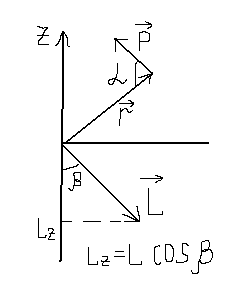=rp=rmv

Момент импульса относительно оси

3.Разобьем вращающееся тело на малые элементы Δm_i. Расстояния до оси вращения обозначим через r_i, модули линейных скоростей – через υ_i. Тогда кинетическую энергию вращающегося тела можно записать в виде:

Физическая величина 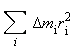зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:

Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:

L = Iω.

Рассмотрим твердое тело вращающееся относительно неподвижной оси. Представим его как систему мат. точек, возьмем i материальную точку.

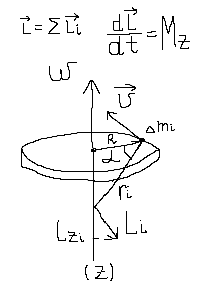
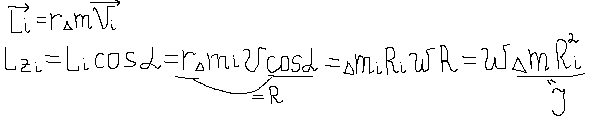
Основной закон динамики вращательного движения твердого тела относительно