ГОС / 28

28. Запишем уравнения Максвелла в вакууме в отсутствии токов и зарядов, то есть при условии :

I. II. (*)-система ДУ в частных производных первого порядка III. IV.

Решение системы (*) в виде постоянных во времени электрических и магнитных полей не представляется возможным. Будем искать решение этих уравнений в виде переменных во времени и пространстве полей.

а) II (возьмем операцию rot от обеих частей уравнения II)

(1.1) (1.2)

( из I, из III)

(1.3), где с-скорость света в вакууме(1.3) примет вид:

(1.4)- волновое уравнение для вектора напряженности электрического поля.

б) аналогично для :

III (возьмем операцию rot от обеих частей)

, так как из IV , из II , то:

(1.5)

(1.5)-волновое уравнение для вектора индукции магнитного поля.

Вид волновых уравнений для и одинаков. Рассмотрим одномерный случай для некоторой величины U(Z,t)(волна, распространяющаяся вдоль оси Z). Для U(Z,t) волновое уравнение принимает вид:

, так как (1.6)

(1.6)-линейное однородное дифференциальное уравнение второго порядка в частных производных с постоянными коэффициентами гиперболического типа. Решение (1.6) ищем по методу Даламбера:

(1.7) , где и - произвольные функции.

Если и тригонометрические функции, то волны, описываемые ими - монохроматические

Определение 1: Электромагнитная волна называется монохроматической, если и изменяются со временем по гармоническому закону с определенной частотой.

В качестве решения (1.6) рассматриваем монохроматическую волну, распространяющуюся в направлении оси Z:

(1.8)

Вопрос. Ур-е (1.6) – ур-е гиперболического типа, т.к. определитель ур-я:

(1.8)-монохроматическая волна с частотой , представляющая собой суперпозицию двух волн.

и - амплитуды этих волн. Выражение, стоящее под знаком cos- фаза волны: , (1.9)

а) зафиксируем для определения распространения волны вдоль Z:

()

, то есть 1-е слагаемое решения (1.8) описывает волну, распространяющуюся в положительном направлении оси Z

б)

, т.е. второе слагаемое в

отрицательном направлении оси Z.

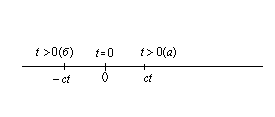
Определение 2: Волновая поверхность- совокупность точек волны, имеющих в данный момент времени одинаковую фазу волны.

-волновое число

(1.10)

Значит,

Рассмотрим трёхмерный случай. Вместо и введём . В данном случае под понимают проекцию или проекцию на произвольное направление. Тогда волновое уравнение запишется

(1)

Решение можно выбрать в виде плоской монохроматической волны

(2)

и - амплитуды волн, а выражения под знаками косинуса в выражении для плоской монохроматической – фазы волн.

Покажем, что (2) решение (1).

*

**

(3)

- плоская монохроматическая волна;

;

Именно при этом условии решение волнового уравнения представляет собой плоскую монохроматическую волну. Данное условие называется законом дисперсии. При выборе решения предполагалось, что вектор - некоторый постоянный вектор.

Покажем, что (2) – плоская монохроматическая волна. Рассмотрим первое слагаемое. Выражение под косинусом – фаза первой волны, распространяющейся в положительном направлении волнового вектора.

Зафиксируем фазу первой волны ()

Введем обозначения , , ,

- уравнение плоскости. Физически это значит, что совокупность точек волны, имеющих одинаковую фазу, лежат на плоскости, а точки волны с одинаковой фазой составляют волновую поверхность. Волновая поверхность данной волны представляет собой плоскость.

Первое слагаемое описывает волну с плоской волновой поверхностью. Это плоская монохроматическая волна, распространяющаяся в положительном направлении вектора .

Т.к - компоненты вектора нормали к данной плоскости, то

- компоненты , который перпендикулярный волновой поверхности.

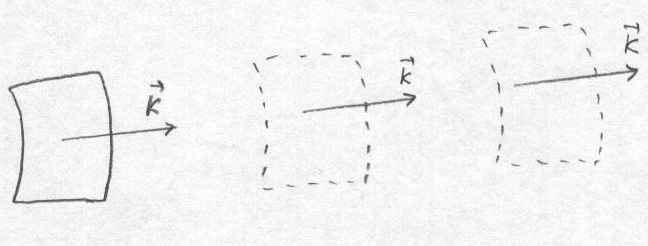
зависит от времени.

Эта зависимость приводит к тому, что волновая поверхность с течением времени перемещается параллельно самой себе в пространстве в направлении .

- плоская монохроматическая волна, распространяющаяся в произвольном направлении. Данное решение можно представить в тригонометрическом виде .

Реальный физический смысл только у первого слагаемого.

Функция косинус является четной. , поэтому

Для волновое уравнение имеет вид

- плоская монохроматическая волна, распространяющаяся вдоль .

указывает направление, вдоль которого колеблется . Модуль этого вектора является амплитудным значением вектора напряженности электрического поля в волне. определяет направление поляризации волны. Если - постоянный вектор, то имеет единственное направление и описывает плоскую монохроматическую линейно поляризованную волну. Если имеет всевозможные направления, то такой свет называется естественным. Для аналогично.

Вопрос Какую роль выполняет ?

1.не имеет физического смысла

2.амплитудное значение

3.указывает направление распространения

4.указывает направление поляризации

- ΙΙ уравнение Максвелла в дифференциальной форме.

Вектора в электромагнитной форме- плоская монохроматическая волна.

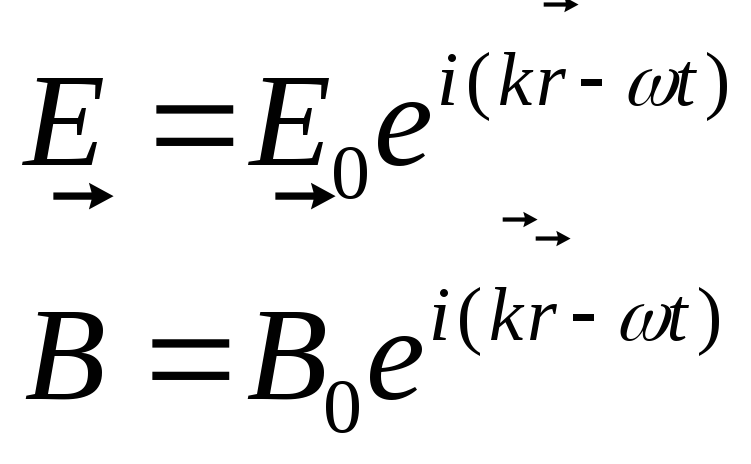(2.1)

(2.2)

Подставляем вектора ив форме (2.1),(2.2) подставим во ΙΙ уравнение Максвелла в дифференциальной форме.

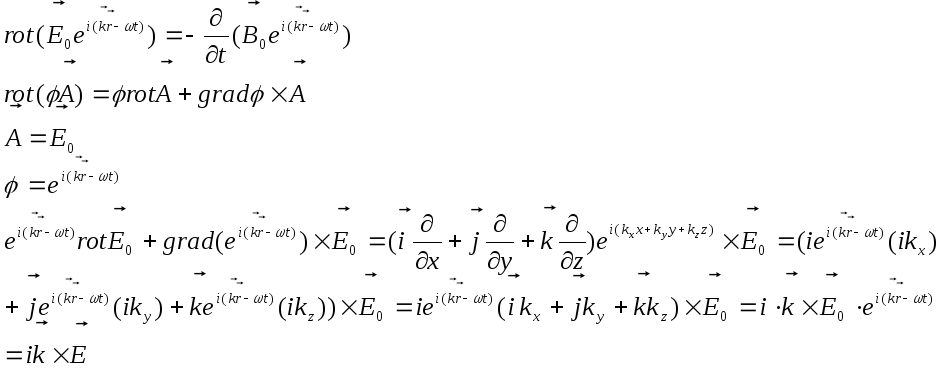
(2.4) 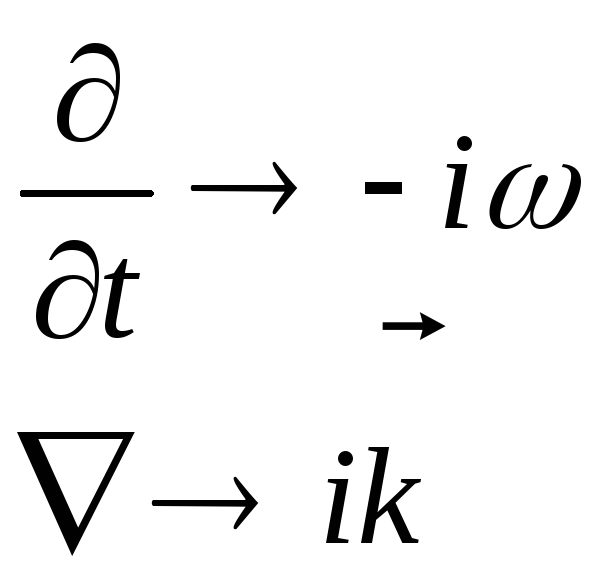(2.7),(2.5)

(2.6)

(2.6)и(2.4) подставим в (2.3)

(2.8)

Согласно векторному произведению

Рассмотрим III уравнение Максвелла

Учитывая (2.5) можем записать

(*)

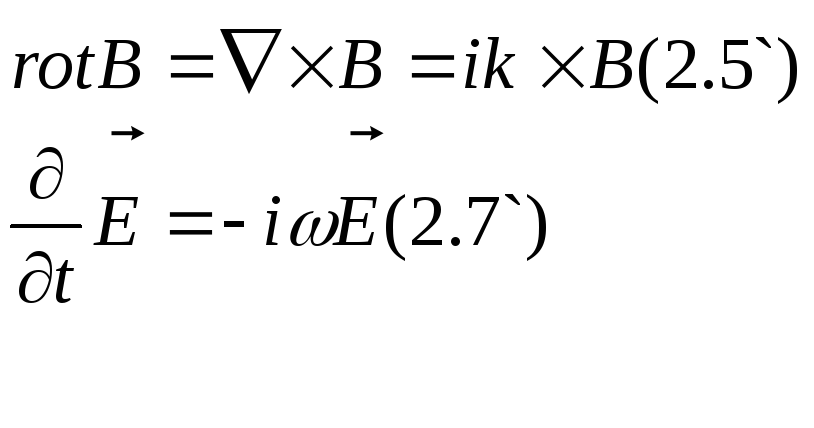
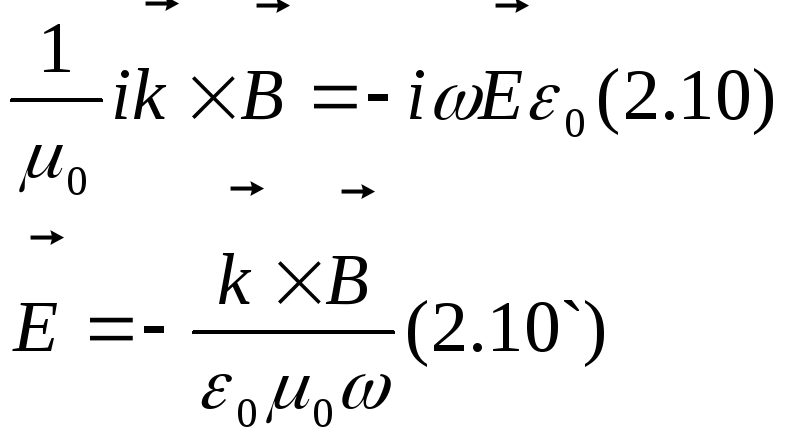
Преобразуем (2.10`) используя (*) (2.10``)

Согласно (2.10)и (2.10``) мы видим, что

Таким образом в плоской монохроматической электромагнитной волне вектора взаимоперпендикулярны, то есть вектор напряжённости электрического и вектора индукции магнитного поля колеблется в плоскости перпендикулярной волновому вектору, плоская монохроматическая электромагнитная волна является поперечной.

Кроме того (2.8) и (2.10``) говорят о том, что составляют правую тройку векторов.

Если посмотреть с начала вектора ,то вращение кпроисходит против часовой стрелки.

.

1. Инвариантность плоской волны.

Из первого инварианта следует, что плоская электромагнитная волна, для которой , т. е. и (6.1), во всех системах координат остается плоской.

Для плоской электромагнитной волны имеем:

(6.2)

и являются амплитудами волны, а выражения, стоящие под знаком косинуса – фазой волны: (6.3). Фаза плоской монохроматической волны является инвариантной, т. е. не меняется при преобразованиях Лоренца.

С одной стороны - это скаляр, скаляр инвариантен относительно преобразований Лоренца. С другой стороны:

(6.4)

Так как , следовательно, (6.4) будет выполняться в том случае, если выражения, стоящие под знаком косинуса, будут равны или отличаться на (). Т. е. действительно, фаза волны инвариантная величина.

2. Четырехмерный волновой вектор.

(6.5)

(6.5) можно представить в виде скалярного произведения двух четырехмерных векторов:

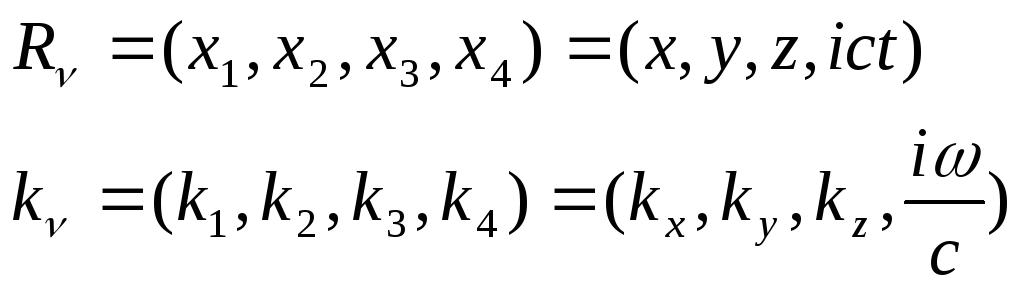(6.7)

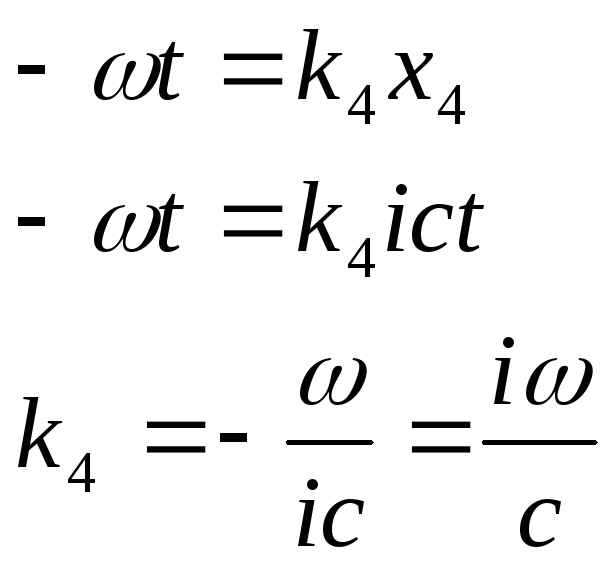(6.6) Четырехмерный вектор называется четырехмерным волновым вектором. Три компоненты этого вектора представляют собой компоненты трехмерного волнового вектора, а четвертая с точностью до постоянной () является частотой.

Получим формулы преобразования компонент волнового вектора при переходе от одной системы координат к другой. Воспользуемся следующей формулой:

:

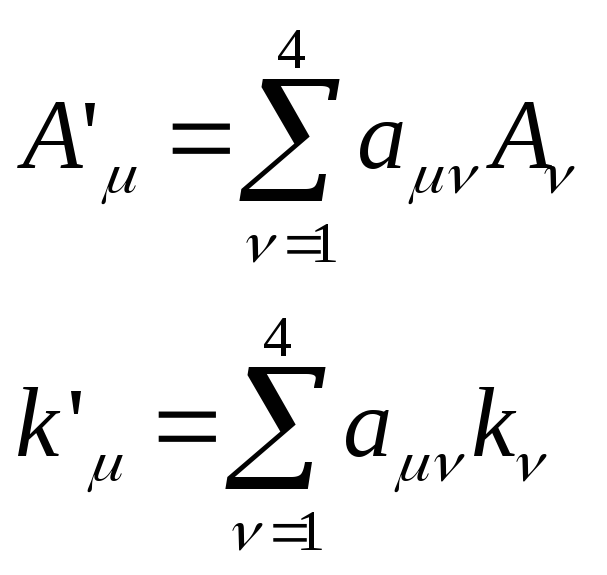
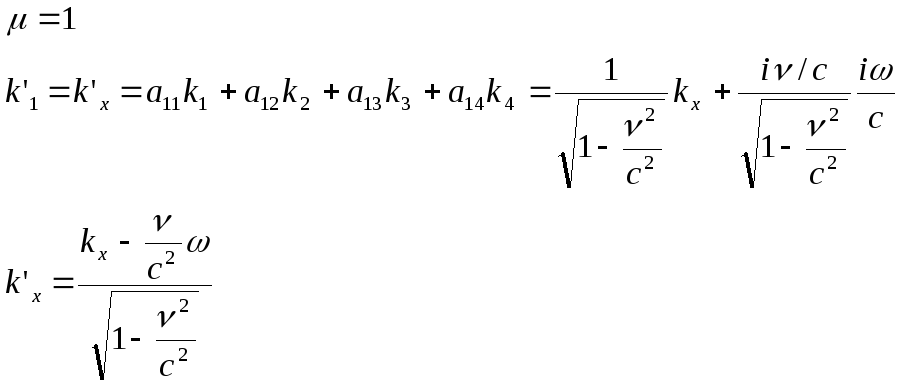
(6.8) 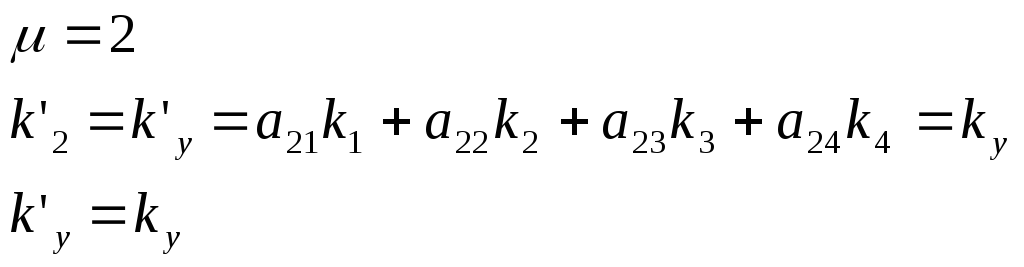(6.9)

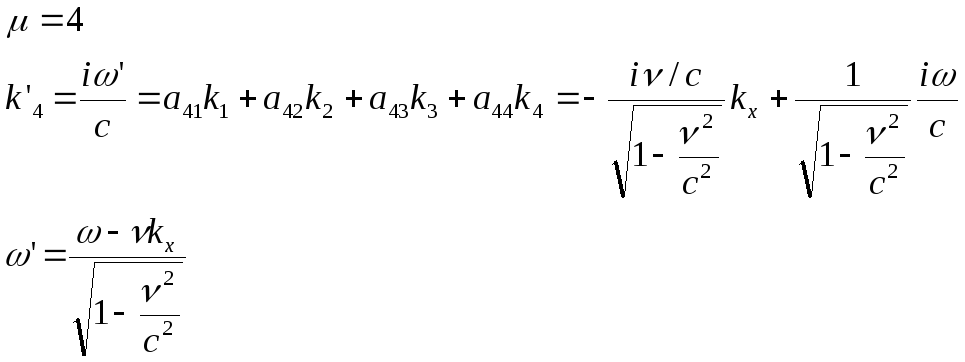
(6.11)

Получили компоненты четырехмерного волнового вектора.

(6.8 - 6.11) – принято записывать в другом виде.

Введем единичный вектор в направлении распространения плоской волны,

т. е. .

(6.12)

(6.12’)

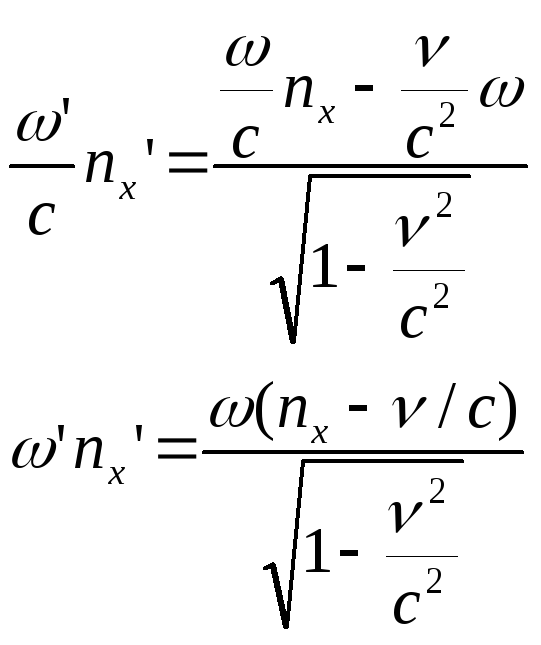
(6.9’)

(6.10’)

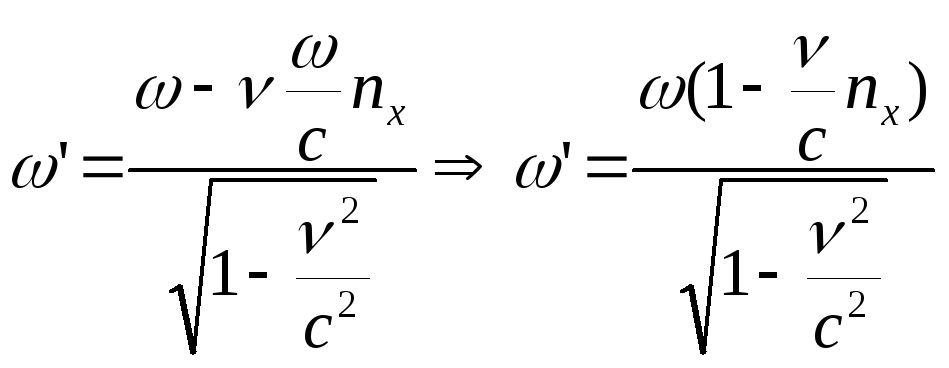
(6.8’) (6.11’)

3. Эффект Допплера.

Эффект Допплера состоит в изменении частоты света в зависимости от движения излучающего источника. Формула (6.11’) и описывает эффект Допплера. Она отличается от классической наличием в знаменателе корня , который учитывает релятивистское замедление времени движущегося излучателя.

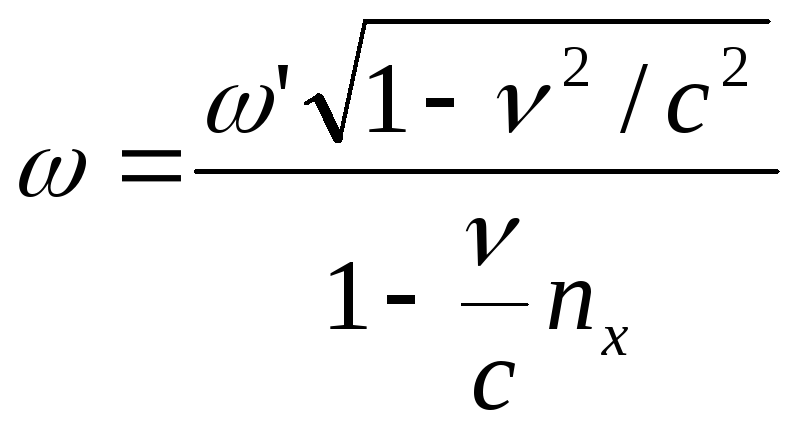(6.12)

(6.13)

Из (6.13) следует, что является косинусом угла между направлением движения светового луча и осью .

Рассмотрим продольный эффект Допплера. Если направление светового луча совпадает с осью , т. е. с направлением движения источника, то получится формула, известная для классического эффекта Допплера.

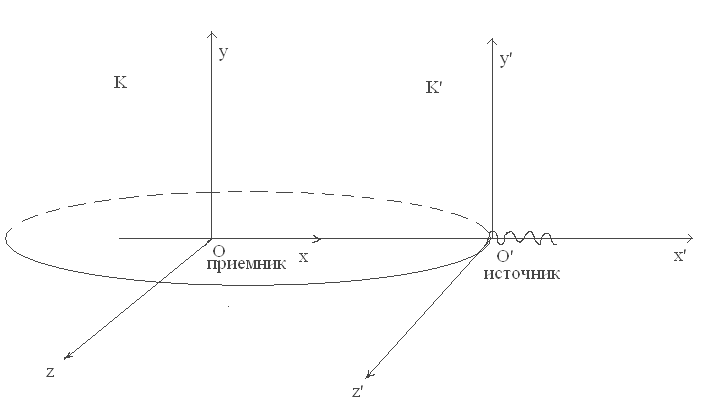
Пусть источник световых волн находится в начале K’, а приемник в начале K.

(6.12) запишется следующим образом:

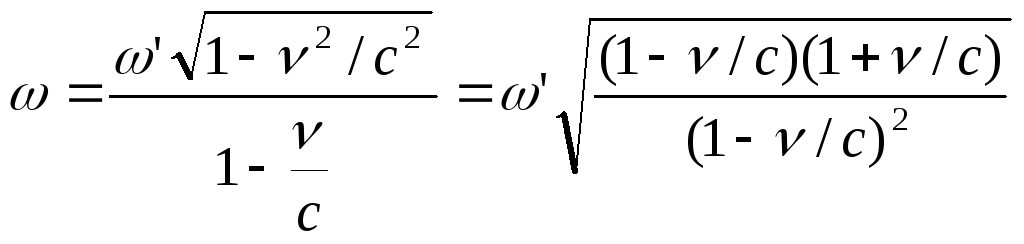(6.14) (6.14’)

Введем обозначение: , тогда .

Разложим эту функцию в ряд:

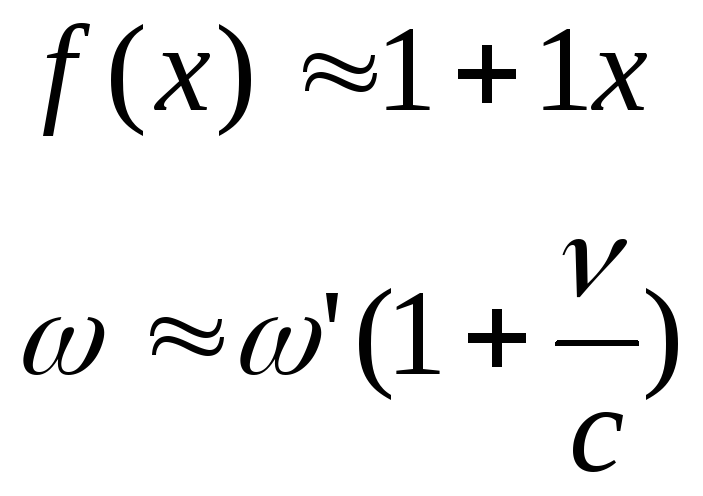(6.15)

Пусть . Тогда (6.14’’) (6.15’)

(6.15 - 6.15’) описывают классический продольный эффект Допплера. Из этих выражений видно, что допплеровское смещение частоты световых волн определяется только относительной скоростью источника и приемника.

Когда .

Поперечный эффект Допплера наблюдается в случае, когда источник излучения движется в направлении перпендикулярном направлению наблюдателя.

Поперечный эффект Допплера заключается в уменьшении воспринимаемой приемником частоты. Рассмотрим этот эффект, предполагая, что источник движется по окружности, в центре которой находится приемник.

(6.16)

(6.17)

Видим, что в выражении (6.17) имеется эффект второго порядка малости по отношению к . Он обусловлен релятивистским множителем и является чисто релятивистским эффектом, связанным с замедлением времени движущегося излучателя.

Экспериментально эффект Допплера (как продольный, так и поперечный) подтвердили опыты Айвса в 1938г. Айвс пользовался излучением атомов водорода, движущихся со скоростями м/c.

.

Он наблюдал наличие релятивистского члена в эффекте Допплера в направлении движения и против направления движения источника.

В эксперименте наблюдались две линии с частотами (6.14’) и (6.14’’). Обе эти линии, а также линии покоящегося атома () фотографировались на одной и той же пластинке. Средняя частота смещения имела множитель. Т. е. опыты Айвса дали подтверждение как продольному, так и поперечному эффекту Допплера.