
Контрольная работа №2.
Задание № 1.Найти неопределенные интегралы.
1.1 1)
![]() ; 1.2 1)
; 1.2 1)![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
4)
![]() ; 4)
; 4)![]() ;
;
5)
![]() . 5)
. 5)![]() .
.
1.3 1)
![]() ; 1.7 1)
; 1.7 1)![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
4)
![]() ;4)
;4)![]() ;
;
5)
![]() .5)
.5)![]() .
.
1.4 1)
![]() ;1.8 1)
;1.8 1)![]() ;
;
2)
![]() ;2)
;2)![]() ;
;
3)
![]() ;3)
;3)![]() ;
;
4)
![]() ;4)
;4)
![]() ;
;
5)
![]() .5)
.5)![]() .
.
1.5 1)
![]() ;1.9 1)
;1.9 1)![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
4)
![]() ; 4)
; 4)![]() ;
;
5)
![]() . 5)
. 5)![]() .
.
1.6 1)
![]() ; 1.10 1)
; 1.10 1)![]() ;
;
2)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 3)
; 3)![]() ;
;
4)![]() ; 4)
; 4)
![]() ;
;
5)
![]() . 5)
. 5)![]() .
.
1.111)![]() ; 1.15 1)
; 1.15 1)![]() ;
;
2)![]() ; 2)
; 2)![]() ;
;
3)
![]() ;3)
;3)![]() ;
;
4)![]() ; 4)
; 4)
![]() ;
;
5)![]() . 5)
. 5)![]() .
.
1.121)![]() ; 1.16 1)
; 1.16 1)![]() ;
;
2)![]() ; 2)
; 2)![]() ;
;
3)
![]() ;3)
;3)![]() ;
;
4)![]() ; 4)
; 4)
![]() ;
;
5)![]() . 5)
. 5)![]() .
.
1.131)![]() ; 1.17 1)
; 1.17 1)![]() ;
;
2)![]() ;2)
;2)![]() ;
;
3)
![]() ;3)
;3)![]() ;
;
4)
![]() ;4)
;4)![]() ;
;
5)![]() .5)
.5)![]() .
.
1.14 1)![]() ;1.18 1)
;1.18 1)![]() ;
;
2)![]() ;2)
;2)![]() ;
;
3)
![]() ;3)
;3)
![]() ;
;
4)
![]() ;4)
;4)
![]() ;
;
5)![]() .5)
.5)![]() .
.
1.19 1)![]() ; 1.20 1)
; 1.20 1)![]() ;
;
2)![]() ;2)
;2)![]() ;
;
3)
![]() ;3)
;3)![]() ;
;
4)
![]() ;4)
;4)
![]() ;
;
5)![]() .5)
.5)![]() .
.
Задание № 2. Вычислить площади фигур, ограниченных линиями.
2.1 1) y = x 3, y = 8,x = 0.
2)
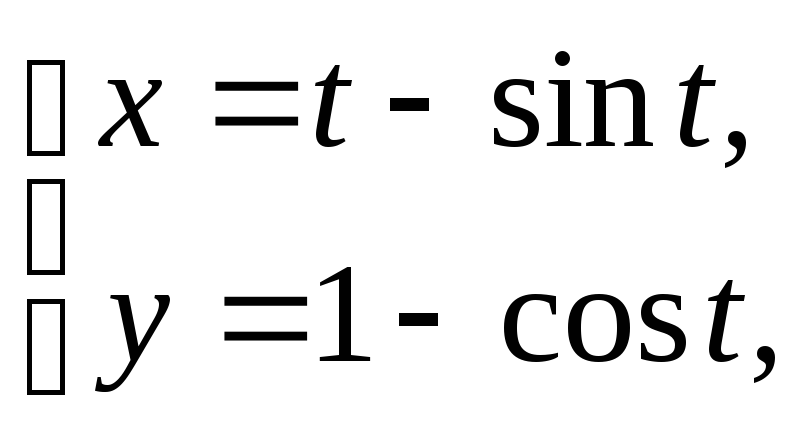 y = 0 (0
≤x≤ 2 π,y0).
y = 0 (0
≤x≤ 2 π,y0).
2.2 1) y = x
2,![]() ,y =2x.
,y =2x.
2)
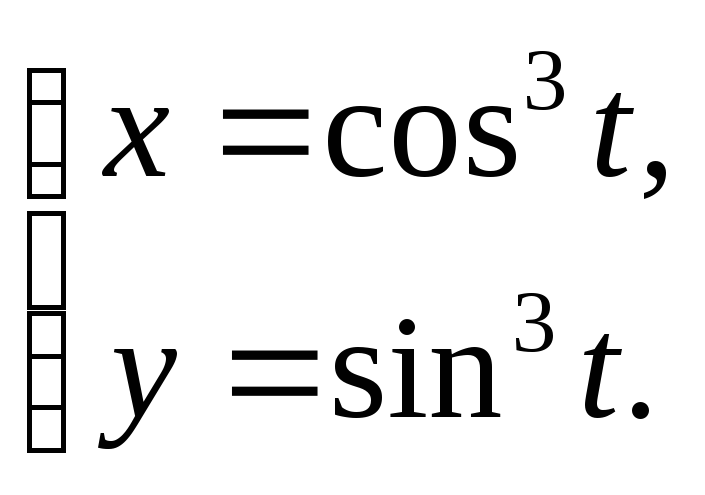
2.3 1) y 3 = x,y =1,x= 8.
2)
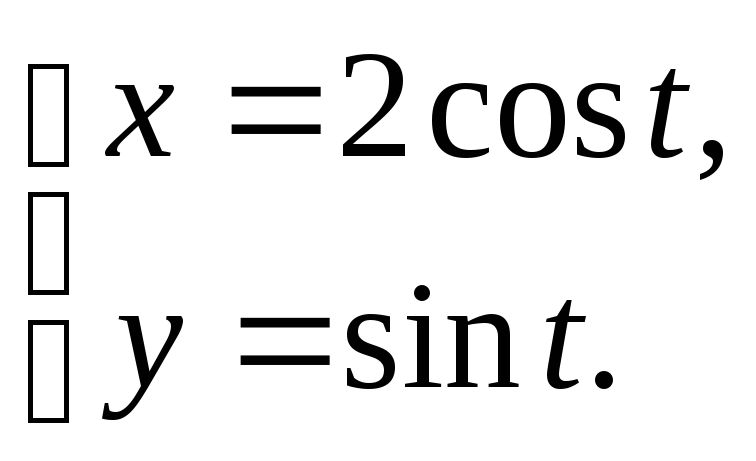
2.4 1) y = ln x, x = e, y =0.
2)
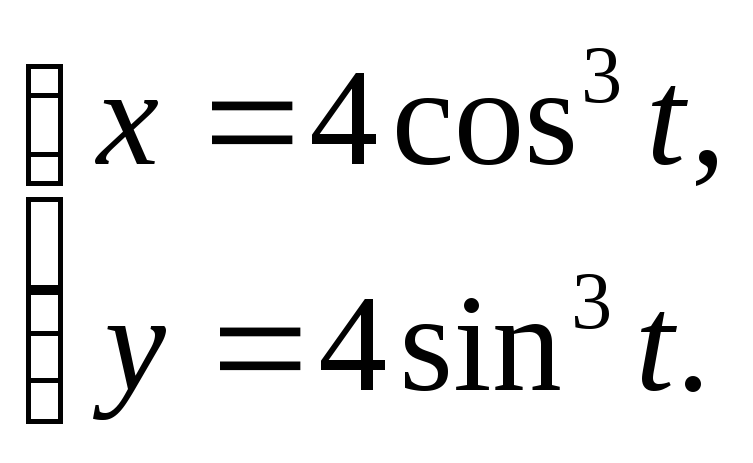
2.5 1) x y = 6,x+y – 7 = 0.
2.
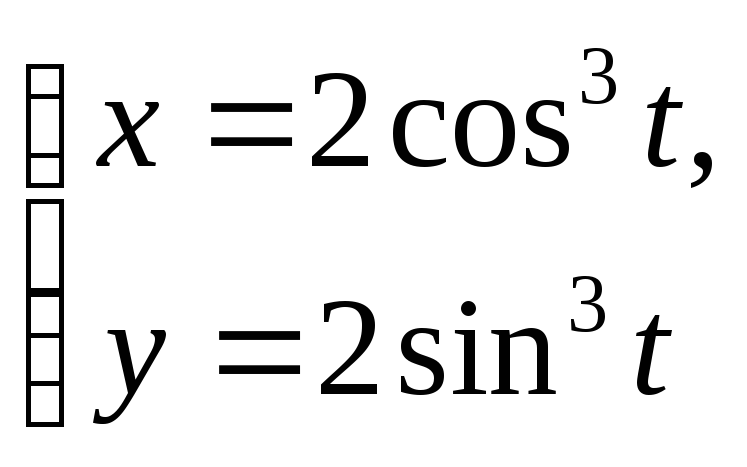 ,x= 0 (x
0),y
=0 (y0).
,x= 0 (x
0),y
=0 (y0).
2.6 1) y = x 2+ 1,x+y= 3.
2)
![]() .
.
2.7 1) y = 0,y =(x+ 1) 2,y =5 –x.
2)
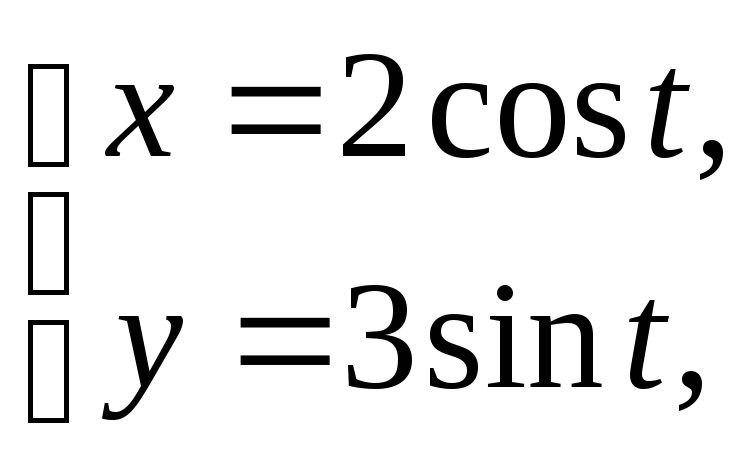 x= 0 (x
0),y
=0 (y0).
x= 0 (x
0),y
=0 (y0).
2.8 1) y 2 = 2x+ 1,x–y – 1=0.
2.
![]() .
.
2.9 1) y = x
2,![]() .
.
2)
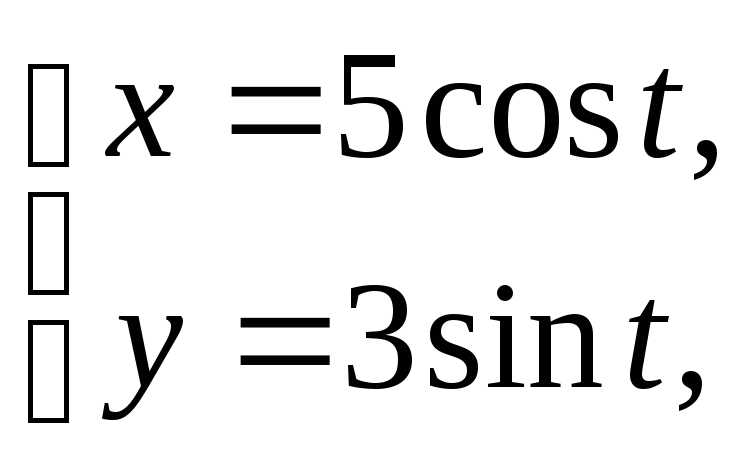 y =0
(y³0).
y =0
(y³0).
2.10 1) x2 +y 2 = 16,y 2= 6x.
2)
![]() .
.
2.11 1) y = x
2,![]() .
.
2)
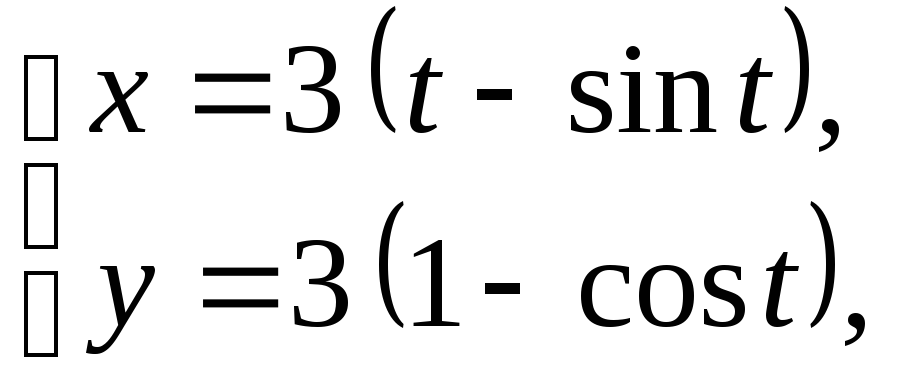 y= 0 (0 ≤x≤ 6 π,y³0).
y= 0 (0 ≤x≤ 6 π,y³0).
2.12 1) x2 +y 2 = 8, 2y = x 2.
2)
![]() .
.
2.13 1) y = x
2,![]() .
.
2)
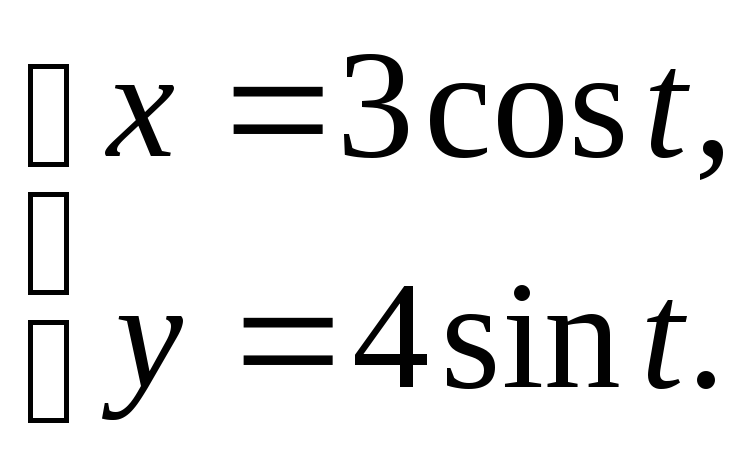
2.14 1) y = x 2,y = x 3.
2) r = 5 φ(0 ≤φ≤ 2 π).
2.15 1) y =e x,y =e – x,x= 1.
2)
![]() .
.
2.16 1) y 2= 2x + 1,x–y– 1 = 0.
2)
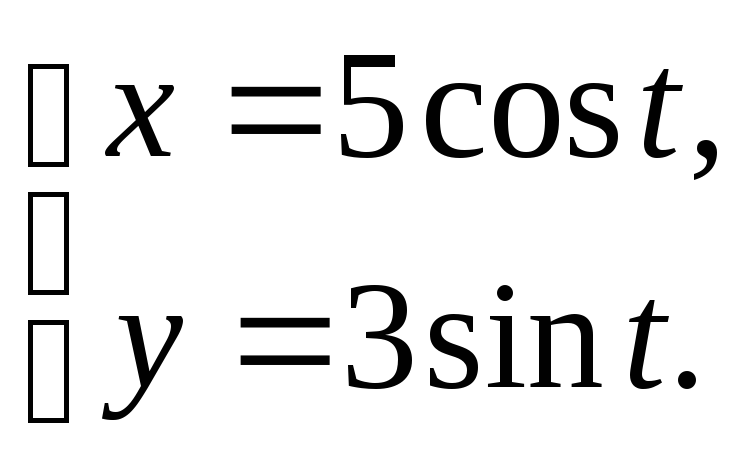
2.17 1) y =sin x,y = cos x, x = 0.
2)
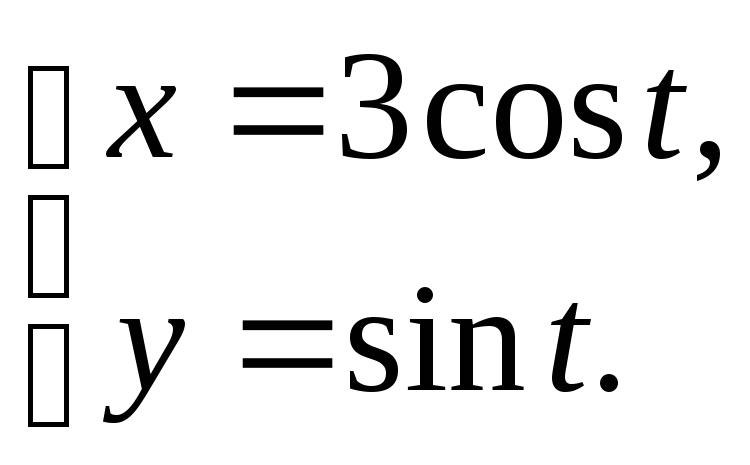
2.18 1) 4 x = y 2, 4y = x 2.
2)
![]() .
.
2.19 1) x= 2 –y –y 2,x= 0.
2.
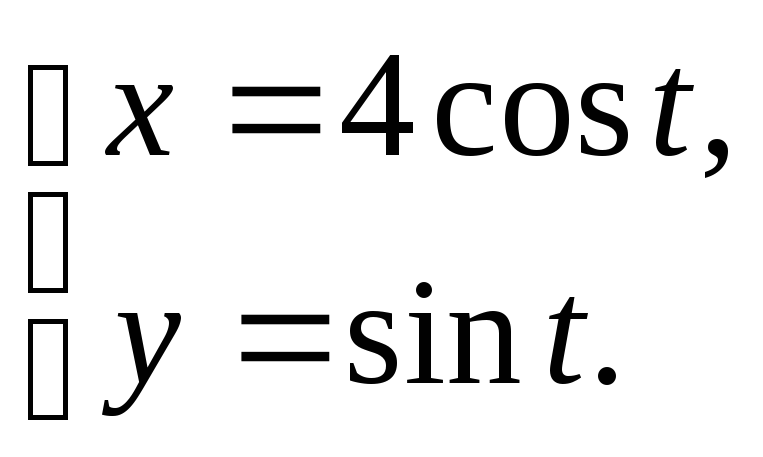
2.20 1) y =x 2– 3x,y + 3x– 4 = 0.
2) tg φ = 1, r = 3,φ= 0.
Задание № 3.
Из урны, содержащей p 1 белых иp 2черных шаров, наудачу извлекаютp шаров. Найти вероятность того, что среди них
ровно kбелых шаров;
хотя бы один белый шар.
(Исходные данные задания 3 в таблице 1)
Таблица 1
-
№ варианта
p 1
p 2
p
k
№ варианта
p 1
p 2
p
k
1
6
4
4
2
11
6
3
4
2
2
6
4
3
2
12
6
3
5
3
3
7
3
5
3
13
7
2
3
2
4
6
4
5
3
14
5
3
4
2
5
7
4
5
2
15
4
4
5
2
6
8
3
4
3
16
5
3
4
3
7
7
4
5
3
17
5
5
6
4
8
5
7
8
3
18
7
3
7
5
9
3
9
8
2
19
7
3
6
4
10
4
8
5
2
20
6
6
8
4
Задание № 4.
Два друга условились о встрече в промежутке времени от Т 1доТ 2. Пришедший первым ждет друга в течениеtминут, после чего уходит. Найти вероятность того, что встреча состоится. (Исходные данные задания 4 в таблице 2).
Таблица 2
|
№ варианта
|
Т 1 (в час. и мин.) |
Т 2 (в час. и мин.) |
t ( в мин.) |
№ варианта
|
Т 1 (в час. и мин.) |
Т 2 (в час. и мин.) |
t ( в мин.) |
|
1 |
9.00 |
11.00 |
20 |
11 |
13.00 |
14.00 |
10 |
|
2 |
10.00 |
11.00 |
10 |
12 |
18.00 |
19.00 |
10 |
|
3 |
10.00 |
12.00 |
20 |
13 |
17.00 |
18.00 |
10 |
|
4 |
11.00 |
12.00 |
15 |
14 |
17.00 |
19.00 |
20 |
|
5 |
11.00 |
13.00 |
15 |
15 |
19.00 |
20.00 |
15 |
|
6 |
9.00 |
11.30 |
20 |
16 |
19.00 |
21.00 |
15 |
|
7 |
10.00 |
11.30 |
15 |
17 |
17.00 |
17.30 |
10 |
|
8 |
11.00 |
11.30 |
5 |
18 |
16.00 |
17.30 |
15 |
|
9 |
12.00 |
13.00 |
5 |
19 |
17.00 |
17.30 |
5 |
|
10 |
12.00 |
12.30 |
10 |
20 |
16.00 |
16.30 |
10 |
Задание № 5.
В k - ой(k = 1, 2, 3) группе факультета учатсяn kчеловек, среди которыхm k %иногородних. Выбранный наудачу студент оказался иногородним. Найти вероятность того, что он учится вi– ой группе. (Исходные данные задания 5 приведены в таблице 3).
Таблица 3
|
№ варианта
|
n 1
|
n 2
|
n 3
|
m 1
|
m 2
|
m 3
|
i |
№ варианта
|
n 1
|
n 2
|
n 3
|
m 1
|
m 2
|
m 3
|
i |
|
1 |
25 |
24 |
23 |
60 |
70 |
80 |
3 |
11 |
19 |
21 |
24 |
10 |
20 |
30 |
3 |
|
2 |
25 |
24 |
23 |
60 |
70 |
80 |
2 |
12 |
19 |
21 |
24 |
10 |
20 |
30 |
1 |
|
3 |
25 |
24 |
23 |
60 |
70 |
80 |
1 |
13 |
17 |
18 |
21 |
20 |
60 |
40 |
3 |
|
4 |
21 |
22 |
21 |
50 |
60 |
70 |
1 |
14 |
17 |
18 |
21 |
20 |
60 |
40 |
2 |
|
5 |
21 |
22 |
21 |
50 |
60 |
70 |
2 |
15 |
20 |
22 |
24 |
70 |
40 |
80 |
3 |
|
6 |
21 |
22 |
21 |
50 |
60 |
70 |
3 |
16 |
20 |
22 |
24 |
70 |
40 |
80 |
1 |
|
7 |
20 |
23 |
21 |
30 |
60 |
50 |
3 |
17 |
20 |
22 |
24 |
70 |
40 |
80 |
2 |
|
8 |
20 |
23 |
21 |
30 |
60 |
50 |
1 |
18 |
26 |
20 |
22 |
90 |
70 |
90 |
1 |
|
9 |
20 |
23 |
21 |
30 |
60 |
50 |
2 |
19 |
26 |
20 |
22 |
90 |
70 |
90 |
3 |
|
10 |
19 |
21 |
24 |
10 |
20 |
30 |
2 |
20 |
26 |
20 |
22 |
90 |
70 |
90 |
2 |
Задание № 6.
Случайная величина Хподчиняется закону арксинуса с плотностью распределения вероятностей
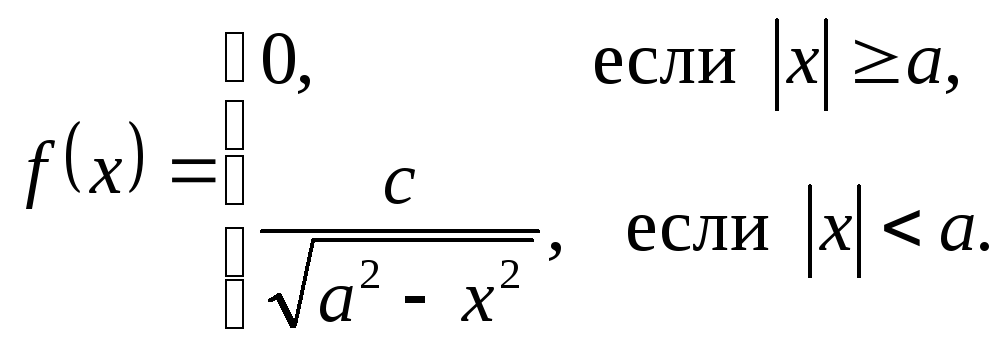
Найти: 1) постоянную с;
2) функцию распределения случайной величины Х.
(Исходные данные задания 6 приведены в таблице 4)
Таблица 4
-
№
варианта
a
№
варианта
a
№
варианта
a
№
варианта
a
1
0,1
6
0,6
11
1,1
16
1,6
2
0,2
7
0,7
12
1,2
17
1,7
3
0,3
8
0,8
13
1,3
18
1,8
4
0,4
9
0,9
14
1,4
19
1,9
5
0,5
10
1
15
1,5
20
2
Задание № 7.
Для случайной величины Хзадания № 6 построить графики функции распределения F(x) и плотности распределения вероятностей f(x).
Задание № 8.
Для случайной величины Хзадания № 6 вычислить:
1) математическое ожидание;
2) дисперсию;
3) моду;
4) медиану.
5) вероятность выполнения неравенства
![]()
Задание № 9.
Дискретная случайная величина Хзадана законом распределения вероятностей. Вычислить дисперсию этой случайной величины.
9.1
|
X |
– 1 |
2 |
4 |
|
P |
p 1 |
0,2 |
0,3 |
9.2
|
X |
– 1 |
2 |
4 |
|
P |
p 1 |
0,3 |
0,4 |
9.3
|
X |
– 1 |
2 |
4 |
|
P |
p 1 |
0,4 |
0,2 |
9.4
|
X |
– 2 |
2 |
6 |
|
P |
0,1 |
p 2 |
0,2 |
9.5
|
X |
– 2 |
2 |
6 |
|
P |
0,4 |
p 2 |
0,1 |
9.6
|
X |
– 2 |
2 |
6 |
|
P |
0,3 |
p 2 |
0,1 |
9.7
|
X |
1 |
3 |
5 |
|
P |
0,7 |
0,1 |
p 3 |
9.8
|
X |
1 |
3 |
5 |
|
P |
0,6 |
0,2 |
p 3 |
9.9
|
X |
1 |
2 |
3 |
|
P |
0,3 |
0,1 |
p 3 |
9.10
|
X |
2 |
5 |
8 |
|
P |
p 1 |
0,2 |
0,1 |
9.11
|
X |
2 |
5 |
8 |
|
P |
p 1 |
0,3 |
0,2 |
9.12
|
X |
2 |
5 |
8 |
|
P |
p 1 |
0,4 |
0,2 |
9.13
|
X |
– 3 |
1 |
5 |
|
P |
0,2 |
p 2 |
0,3 |
9.14
|
X |
– 3 |
1 |
5 |
|
P |
0,1 |
p 2 |
0,2 |
9.15
|
X |
– 3 |
1 |
5 |
|
P |
0,5 |
p 2 |
0,1 |
9.16
|
X |
– 4 |
1 |
6 |
|
P |
0,2 |
0,3 |
p 3 |
9.17
|
X |
– 4 |
1 |
6 |
|
P |
0,4 |
0,1 |
p 3 |
9.18
|
X |
– 4 |
1 |
6 |
|
P |
0,6 |
0,3 |
p 3 |
9.19
|
X |
3 |
4 |
5 |
|
P |
p 1 |
0,2 |
0,7 |
9.20
|
X |
3 |
4 |
5 |
|
P |
0,4 |
p 2 |
0,3 |
Задание № 10. Непрерывная случайная величинаX распределена нормально с известными параметрамиm и . Найти вероятность попадания этой величины в заданный интервал (x 1, x 2).
(Исходные данные задания 10 приведены в таблице 5).
Таблица 5
|
№ варианта |
m |
|
x 1 |
x 2 |
|
1 |
10 |
4 |
2 |
13 |
|
2 |
9 |
5 |
5 |
14 |
|
3 |
8 |
1 |
4 |
9 |
|
4 |
7 |
2 |
3 |
10 |
|
5 |
6 |
3 |
2 |
11 |
|
6 |
5 |
1 |
1 |
12 |
|
7 |
4 |
5 |
2 |
11 |
|
8 |
3 |
2 |
3 |
10 |
|
9 |
2 |
5 |
4 |
9 |
|
10 |
10 |
4 |
2 |
13 |
|
11 |
7 |
2 |
3 |
10 |
|
12 |
2 |
4 |
6 |
10 |
|
13 |
2 |
5 |
4 |
9 |
|
14 |
3 |
2 |
3 |
10 |
|
15 |
4 |
5 |
2 |
11 |
|
16 |
5 |
1 |
1 |
7 |
|
17 |
6 |
3 |
2 |
11 |
|
18 |
7 |
2 |
3 |
10 |
|
19 |
8 |
1 |
4 |
9 |
|
20 |
9 |
5 |
2 |
14 |
Задание № 11.
Время ожидания очереди является случайной величиной X, распределенной по показательному закону со средним временем ожидания, равнымt 0 минут.
Найти вероятность того, что посетитель будет ожидать своей очереди не менее tминут.
(Исходные данные задания 11 приведены в таблице 6).
Таблица 6
|
№ варианта |
t 0 |
t |
№ варианта |
t 0 |
t |
|
1 |
1 |
3 |
11 |
10 |
10 |
|
2 |
2 |
4 |
12 |
9 |
9 |
|
3 |
3 |
3 |
13 |
8 |
8 |
|
4 |
4 |
4 |
14 |
7 |
7 |
|
5 |
5 |
10 |
15 |
6 |
6 |
|
6 |
6 |
18 |
16 |
5 |
5 |
|
7 |
7 |
21 |
17 |
4 |
4 |
|
8 |
8 |
16 |
18 |
3 |
3 |
|
9 |
9 |
27 |
19 |
2 |
2 |
|
10 |
10 |
20 |
20 |
1 |
1 |
Задание № 12.
Cлучайная величинаX распределена равномерно с функцией распределения
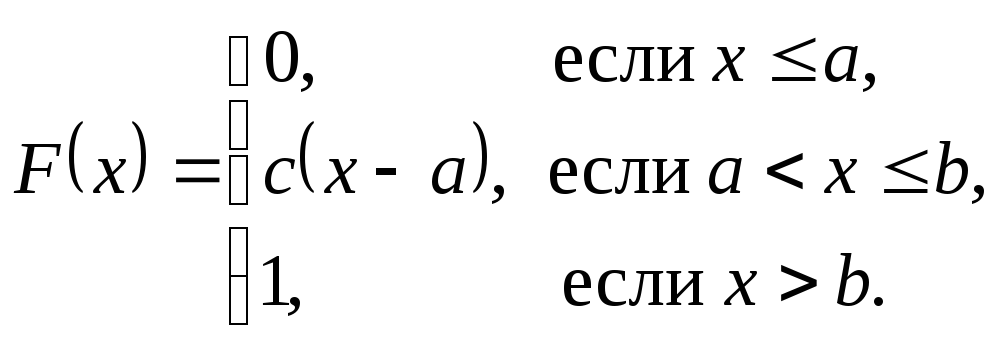
Найти: 1) постоянную с;
2) плотность распределения вероятностей случайной величины X.
(Исходные данные приведены в таблице 7)
Таблица 7
|
№ варианта |
a |
b |
№ варианта |
a |
b |
|
1 |
– 1 |
2 |
11 |
– 2 |
3 |
|
2 |
– 2 |
1 |
12 |
– 3 |
2 |
|
3 |
– 3 |
5 |
13 |
0 |
6 |
|
4 |
2 |
3 |
14 |
1 |
9 |
|
5 |
2 |
4 |
15 |
3 |
11 |
|
6 |
1 |
3 |
16 |
4 |
10 |
|
7 |
1 |
9 |
17 |
2 |
7 |
|
8 |
2 |
8 |
18 |
– 2 |
3 |
|
9 |
3 |
7 |
19 |
– 4 |
0 |
|
10 |
1 |
5 |
20 |
– 5 |
2 |
Задание № 13. Для случайной величиныXзадания 12 вычислить:
математическое ожидание;
дисперсию;
вероятность выполнения неравенства
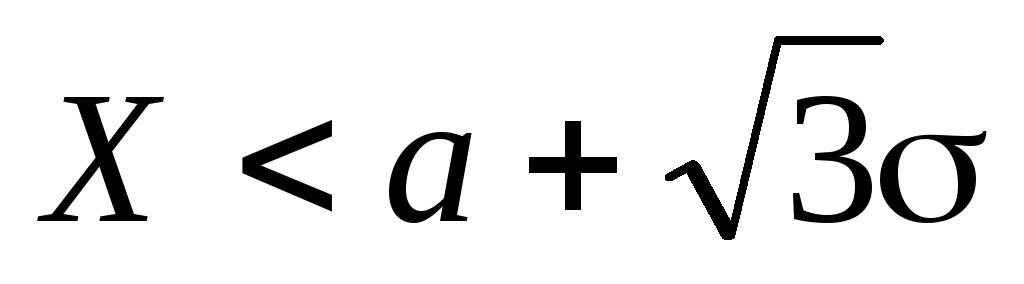 ,среднее квадратическое
отклонение случайной величиныX.
,среднее квадратическое
отклонение случайной величиныX.
