Длина дуги
Кривой
γ в пространстве называется отображение

 .
Здесь t называется параметром. Точка
.
Здесь t называется параметром. Точка называется началом кривой γ , а точка
называется началом кривой γ , а точка называется концом. Если P=Q, то кривая
γ называется замкнутой. Кривая γ
называется непрерывной, если функции
называется концом. Если P=Q, то кривая
γ называется замкнутой. Кривая γ
называется непрерывной, если функции непрерывны. Кривая называется гладкой,
если существуют непрерывные производные
непрерывны. Кривая называется гладкой,
если существуют непрерывные производные ,
причём они не равны 0 одновременно.
Кривая γ называется кусочно-гладкой,
если её можно разбить на конечное число
гладких кусков.
,
причём они не равны 0 одновременно.
Кривая γ называется кусочно-гладкой,
если её можно разбить на конечное число
гладких кусков.
Примеры.
1. Отрезок прямой

2. Окружность
 .
Считая а)
.
Считая а) , б)
, б) , в)
, в) получим разные кривые.
получим разные кривые.
3. Винтовая линия радиуса R и с шагом H

4. Цепная линия - график функции
 .
.
5. Периметр квадрата - пример кусочно
гладкой, но не гладкой кривой
Длина
кривой.Пусть -- точки пространства. Тогда кривую
-- точки пространства. Тогда кривую
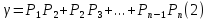
назовём
ломаной, а число
 назовём длиной этой ломаной. Пусть (1)
-- произвольная кривая, и
назовём длиной этой ломаной. Пусть (1)
-- произвольная кривая, и -- разбиение. Обозначим
-- разбиение. Обозначим .
Тогда ломаную
.
Тогда ломаную назовём вписанной в
назовём вписанной в .
Длиной кривой
.
Длиной кривой называется предел длин вписанных
ломаных, если максимум длин звеньев
стремиться к 0.
называется предел длин вписанных
ломаных, если максимум длин звеньев
стремиться к 0.
Теорема. Пусть -- кусочно-гладкая кривая. Тогда
-- кусочно-гладкая кривая. Тогда

Следствие.Если -- дифференцируемая функция с кусочно
непрерывной производной на отрезке
-- дифференцируемая функция с кусочно
непрерывной производной на отрезке ,
то длина дуги графика этой функции на
данном отрезке будет равна
,
то длина дуги графика этой функции на
данном отрезке будет равна

Примеры. 1. Длина отрезкаPQравна

 2.
Длина окружности
2.
Длина окружности

3.
Длина одного витка винтовой линии

4.
Длина цепной
линии




 .
Здесь t называется параметром. Точка
.
Здесь t называется параметром. Точка называется началом кривой γ , а точка
называется началом кривой γ , а точка называется концом. Если P=Q, то кривая
γ называется замкнутой. Кривая γ
называется непрерывной, если функции
называется концом. Если P=Q, то кривая
γ называется замкнутой. Кривая γ
называется непрерывной, если функции непрерывны. Кривая называется гладкой,
если существуют непрерывные производные
непрерывны. Кривая называется гладкой,
если существуют непрерывные производные ,
причём они не равны 0 одновременно.
Кривая γ называется кусочно-гладкой,
если её можно разбить на конечное число
гладких кусков.
,
причём они не равны 0 одновременно.
Кривая γ называется кусочно-гладкой,
если её можно разбить на конечное число
гладких кусков.
 .
Считая а)
.
Считая а) , б)
, б) , в)
, в) получим разные кривые.
получим разные кривые.
 .
. -- точки пространства. Тогда кривую
-- точки пространства. Тогда кривую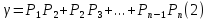
 назовём длиной этой ломаной. Пусть (1)
-- произвольная кривая, и
назовём длиной этой ломаной. Пусть (1)
-- произвольная кривая, и -- разбиение. Обозначим
-- разбиение. Обозначим .
Тогда ломаную
.
Тогда ломаную назовём вписанной в
назовём вписанной в .
Длиной кривой
.
Длиной кривой называется предел длин вписанных
ломаных, если максимум длин звеньев
стремиться к 0.
называется предел длин вписанных
ломаных, если максимум длин звеньев
стремиться к 0. -- кусочно-гладкая кривая. Тогда
-- кусочно-гладкая кривая. Тогда
 -- дифференцируемая функция с кусочно
непрерывной производной на отрезке
-- дифференцируемая функция с кусочно
непрерывной производной на отрезке ,
то длина дуги графика этой функции на
данном отрезке будет равна
,
то длина дуги графика этой функции на
данном отрезке будет равна

 2.
Длина окружности
2.
Длина окружности

