8. Формула Ньютона-Лейбница

Интеграл вида 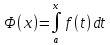называют интегралом с переменным верхним пределом.

Теорема. Пусть непрерывна на отрезке. Тогда есть первообразная функции :

для любого .

Доказательство. Пусть . Тогда по теореме о среднем

для некоторой точкиСледовательно,при, ибо в этом случае, а функциянепрерывна.□

Формула Ньютона-Лейбница. Пусть -- первообразная функции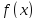. Тогда

9. Замена переменной и интегрирование по частям в определённом интеграле

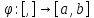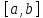Замена переменной. Пусть-- дифференцируемое отображениеcнепрерывной производной и такое, что, а-- непрерывная функция, заданная на отрезке. Тогда

Пример 1.Вычислим площадь верхнего полукруга радиусаR.

Интегрирование по частям. Пустьи-- дифференцируемые функции на отрезке. Тогда

Пример 2.Вычислим

Заметим, что при условии

10. Несобственные интегралы

Пусть функция задана на полуинтервале, где, а величинаможет быть как конечным числом, так и. Предположим, чтоинтегрируема на любом отрезке,. Полагаем по определению

и называем это число несобственным интегралом. В случае, когда предел (1) существует, то говорим, что соответствующий интеграл сходится; в противном случае будем говорить, что онрасходится.

Несобственный интеграл (1) применяется в двух типичных ситуациях.

1) Пусть . Тогда

2) Пусть d∈ℝи функциянеограничена на полуинтервале.

Если на полуинтервале, то несобственный интеграл равен площади неограниченной фигуры -- криволинейной трапеции, ограниченной сверху графиком функции, снизу – осью Ох и слева – вертикальной прямой

Формула Ньютона-Лейбница для несобственных интегралов. Пусть-- первообразная непрерывной функциина интервале (c,d). Предположим, что существуют пределы

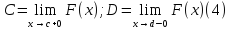
Тогда несобственный интеграл сходится, причём

Равенство (5) вытекает из формулы Ньютона-Лейбница для обычных интегралов и соотношений (4).

Пример. Вычислим

Предложение об "эталонных" интегралах . Пусть a>0.

1. Интеграл сходится тогда и только тогда, когда p>1.

2. Интеграл сходится тогда и только тогда, когдаp<1.

Доказательство. 1. Если, то первообразнаяподинтегральной функцииимеет конечный предел 0 при. По формуле Ньютона-Лейбница для несобственных интегралов, получаем, что интегралсходится и равен.

Если , то первообразной подинтегральной функции служит, который не имеет конечного предела на. Длято же самое можно сказать о первообразной.

Аналогично, прямыми вычислениями доказывает второе утверждение.

Примеры

1. Интегралсходится, так как здесь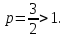

2. Докажем, что интегралы исходятся и вычислим их. Имеем

Интеграл также сходится, ибо занесение под знак дифференциалаи заменапревращают его в интеграл, который сходится согласно предложению об эталонных интегралах и равен 1.

Интегралы ирасходятся, так как такая же замена приводит их к несобственным эталонным интегралами, с

1. Приложение определённого интеграла к вычислению геометрических величин

Площадь плоской фигуры

Пусть криволинейная трапеция задана так: с непрерывной функцией. Тогда площадь S этой криволинейной трапеции равна

Пусть теперь криволинейная трапеция задана так: с непрерывной функцией. Тогда площадь S этой криволинейной трапеции равна

Рассмотрим теперь криволинейную трапецию с непрерывными функциями f(x) и g(x). Тогда площадь S этой криволинейной трапеции равна

2. Полярные координаты

Пусть P -- точка на декартовой плоскости . Обозначим через r=r(P) расстояние от P до начала координат и назовём это число полярным радиусом. Через𝜑=𝜑(P) обозначим угол, на который надо повернуть осьдо совмещения с направлением вектора; эту величину назовём полярным углом. Полярный угол не определен для начала координат. Параназывается полярными координатами точки P. Ясно, что

,

,, еслии, если

3. Площадь криволинейного сектора

Обозначим через Kкриволинейный сектор -- фигуру на плоскости, заданную системой неравенств

(-- непрерывная функция.) Найдём площадьS(K) этого сектора. Для этого обозначим через S(τ ) площадь сектора заданного также как и в (1), но с=τ . Тогда

Отсюда

4. Объём тела

Пусть в пространстве задано тело V и ось Ox; причём тело расположено в полосе a≤ x≤ b. Предположим, что известна площадь сечения тела плоскостью перпендикулярной оси Ox и проходящей через точку x. Обозначим эту площадь S(x). Обозначим через V(x) объем левой части тела V, отсекаемого плоскостью. Тогда δV -- объем слоя от x доОтсюда. Значит

Следствие (принцин Кавальери)Если два тела имеют одинаковые площади сечения на одинаковой высоте, то объёмы этих тел совпадают.

В частности, если V -- тело вращения, т.е. получено вращением криволинейной трапеции , то сечениеплоскостью, проходящей через x и параллельной координатной плоскости OYZ есть круг радиуса. Следовательно, S(x)=π f(x)²в этом случае и объём тела вращения

Примеры 1.Объём шара радиусR. Шар представляем как тело вращения полукруга -R≤ x≤ R;вокруг оси Ox. Тогда

Пример 2. Объём "обобщенного конуса" с площадью основания S и высоты H. Пусть вершина конуса имеет координату 0, а основание имеет координату H. Обозначим площадь сечения плоскостьючерез. Тогда, откуда. Следовательно,

3. Объём обобщённого цилиндра с площадью основания S и высоты H. В обозначениях предыдущего примера имеем S(x)=S. Отсюда