
- •Тема 12 неопределенный интеграл.
- •Первообразная и неопределенный интеграл
- •Простейшие свойства неопределенного интеграла.
- •Замена переменной в неопределённом интеграле
- •Интегрирование иррациональных выражений
- •Интегрирование тригонометрических выражений
- •Тема 13 определенный интеграл Определение определенного интеграла
- •Формула Ньютона-Лейбница
- •Замена переменной и интегрирование по частям в определённом интеграле
- •Несобственные интегралы
- •Приложение определённого интеграла к вычислению геометрических величин
- •Длина дуги
Тема 12 неопределенный интеграл.
Первообразная и неопределенный интеграл
Решаем дифференциальное уравнение

на
интервале
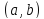 .
Уравнение (1) можно переписать в
дифференциалах:
.
Уравнение (1) можно переписать в
дифференциалах:
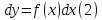
Любое
решение такого уравнения называется
первообразной функции
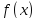 .Первообразная
.Первообразная
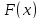 функции
функции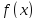 на интервале
на интервале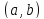 .
Случаи
.
Случаи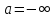 и/или
и/или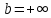 . Ясно, что если
. Ясно, что если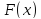 первообразная, то и
первообразная, то и также первообразная. Наша задача –
найти все решения уравнения (1). Функция
двух переменных
также первообразная. Наша задача –
найти все решения уравнения (1). Функция
двух переменных называется общим решением уравнения
(1) или неопределенным интегралом функции
называется общим решением уравнения
(1) или неопределенным интегралом функции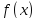 ,
если при подстановке вместо
,
если при подстановке вместо любого числа получаем частное решение
уравнения (1) и любое частное решение
уравнения (1) получается таким образом.
любого числа получаем частное решение
уравнения (1) и любое частное решение
уравнения (1) получается таким образом.
Лемма.
Пусть
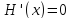 тождественно для всех
тождественно для всех .
Тогда
.
Тогда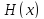 -- константа на этом интервале.
-- константа на этом интервале.
Теорема о первообразных. Две первообразных одной и той же функции, определенной на интервале, отличаются на константу.
Следствие.
Если
 -- первообразная функции
-- первообразная функции ,
то
,
то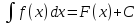 ,
где C пробегает множество действительных
чисел.
,
где C пробегает множество действительных
чисел.
Простейшие свойства неопределенного интеграла.
1. Интеграл от суммы равен сумме интегралов:
2. Константу можно выносить за знак интеграла:
3. Производная от интеграла равна подинтегральной функции.
4. Дифференциал от интеграла равен подинтегральному выражению.
5.
(Линейная замена переменных) Если
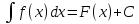 ,
то
,
то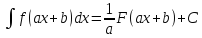 (здесь
(здесь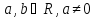 ).
).
Таблица основных интегралов
|
f(x) |
|
|
|
|
|
|
|
|
|
|
F(x) |
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
F(x) |
|
|
|
|
|
|
Замена переменной в неопределённом интеграле
По
определению
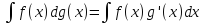 .
.
Теорема.Пусть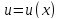 -- дифференцируемая функция. Тогда
-- дифференцируемая функция. Тогда

В
частном случае, когда
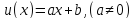 получаем линейную замену переменных
(см. свойство 5,§1).
получаем линейную замену переменных
(см. свойство 5,§1).
Примеры.А.

В.

Г.

Интегрирование по частям в неопределённом интеграле
Теорема.
Для дифференцируемых функций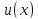 и
и имеет место соотношение
имеет место соотношение
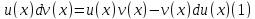
Пример.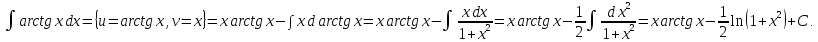
Метод интегрирования функций вида .
.
Пример.
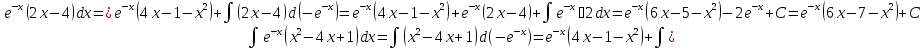
Метод интегрирования функций вида :
:
Пример.

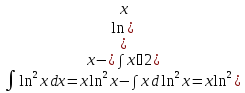
Интегрирование рациональных дробей
Рациональной
дробью называется функция вида
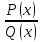 ,
где
,
где – многочлены. Если
– многочлены. Если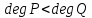 ,
то рациональную дробь
,
то рациональную дробь называют правильной. В противном случае
ее называют неправильной.
называют правильной. В противном случае
ее называют неправильной.
Следующие рациональные дроби называют простейшими
(1
тип)
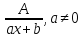 ,
,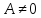
(2
тип)


(3
тип)
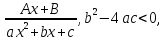

(4
тип)
 ,
,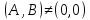
Теорема 1. Любую дробь можно разложить в сумму многочлена и правильной рациональной дроби.
Теорема 2.Любую правильную рациональную дробь можно разложить в сумму простейших.
Примеры.А. Разложим в сумму простейших
в сумму простейших

Отсюда
следует, что
 .
Подставляя в это соотношение
.
Подставляя в это соотношение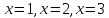 находим сразу
находим сразу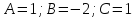 .
Итак
.
Итак

Интегрирование иррациональных выражений
Далее
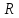 -- рациональная функция одной или
нескольких переменных.
-- рациональная функция одной или
нескольких переменных.
Интегралы вида
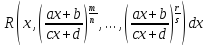
где ad-bc≠ 0, аk=НОК(n,…,s) сводятся к интегралам от рациональной дроби заменой
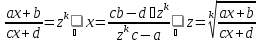
Примеры. А. Вычислим интеграл

Б. Вычислим интеграл
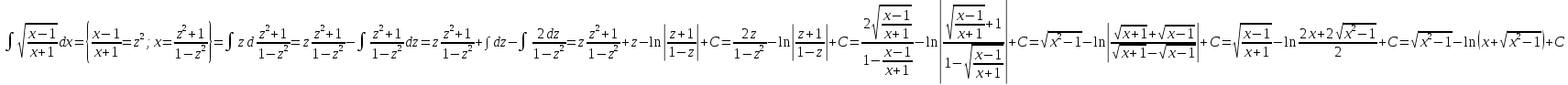
Более простой метод интегрирования (но требующий догадки) этой же функции таков:

Интегрирование тригонометрических выражений
Интегралы
вида
 сводятся к интегралам от рациональной
функции универсальной заменой
сводятся к интегралам от рациональной
функции универсальной заменой
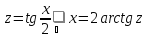
В
частных случаях R(sin x) cos x dx,R(cosx)sinxdxиR(sin2x, cos2x,
tg x, ctg x) dx лучше пользоваться заменами соответственно.
соответственно.
Примеры. А.

Б.
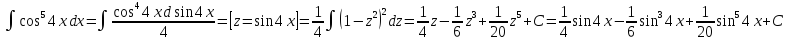
Тема 13 определенный интеграл Определение определенного интеграла
Пусть
функция
 определена на отрезке
определена на отрезке и неотрицательна. Фигура, заданная
неравенствами
и неотрицательна. Фигура, заданная
неравенствами называется криволинейной трапецией.
Вычислим площадь криволинейной трапеции.
Идея вычисления состоит в том, чтобы
нарезать эту трапецию на узенькие
вертикальные полоски, площадь каждой
полоски считать как площадь прямоугольника,
а затем сложить получившиеся результаты.
Мы получим приближенный ответ. Для
получения точного ответа надо брать
полоски все уже и уже и перейти к пределу,
когда максимальная ширина полоски
стремится к нулю.
называется криволинейной трапецией.
Вычислим площадь криволинейной трапеции.
Идея вычисления состоит в том, чтобы
нарезать эту трапецию на узенькие
вертикальные полоски, площадь каждой
полоски считать как площадь прямоугольника,
а затем сложить получившиеся результаты.
Мы получим приближенный ответ. Для
получения точного ответа надо брать
полоски все уже и уже и перейти к пределу,
когда максимальная ширина полоски
стремится к нулю.
Разбиением
отрезка
 называется семейство точек
называется семейство точек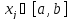 таких, что
таких, что
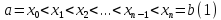
Параметром
разбиения (обозначим его
 )
называется наибольшее из приращений
)
называется наибольшее из приращений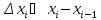 когда индекс
когда индекс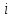 пробегает от 1 до n. Пусть
пробегает от 1 до n. Пусть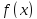 - функция, определенная на отрезке
- функция, определенная на отрезке и
и - какие-либо (отмеченные) точки из отрезков
- какие-либо (отмеченные) точки из отрезков .
Тогда
.
Тогда
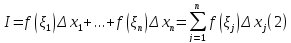
называется интегральной суммой.
Определение.Определённым интегралом функции на отрезке
на отрезке называется предел интегральных сумм,
если параметр разбиения стремиться к
нулю:
называется предел интегральных сумм,
если параметр разбиения стремиться к
нулю:

Если
 ,
то по определению полагаем
,
то по определению полагаем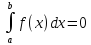 .
Если же
.
Если же ,
то считаем по определению
,
то считаем по определению
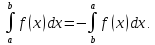
Функция
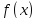 называется подинтегральной,
называется подинтегральной,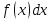 называется подинтегральным выражением.
Число
называется подинтегральным выражением.
Число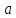 называется нижним пределом интегрирования,
а
называется нижним пределом интегрирования,
а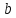 – верхним пределом интегрирования.
– верхним пределом интегрирования.
Функцию
 ,
заданную на отрезке
,
заданную на отрезке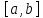 ,
для которой предел (3) существует, назовем
интегрируемой (по Риману) на этом отрезке.
Сумма интегрируемых функций есть
интегрируемая функция и произведение
интегрируемой функции на число есть
также интегрируемая функция. Если
,
для которой предел (3) существует, назовем
интегрируемой (по Риману) на этом отрезке.
Сумма интегрируемых функций есть
интегрируемая функция и произведение
интегрируемой функции на число есть
также интегрируемая функция. Если интегрируемы, то для любых чисел
интегрируемы, то для любых чисел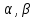 линейная комбинация
линейная комбинация также интегрируема на отрезке
также интегрируема на отрезке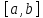 и
и
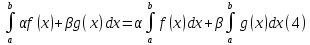
Заметим,
что из определения интеграла, у которого
нижний предел больше или равен верхнему
вытекает, что равенство (4) справедливо
вне зависимости от расположения точек
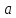 и
и на числовой прямой.
на числовой прямой.
На
существование и на значение определенного
интеграла не влияет изменение значения
функции
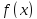 в конечном числе точек.
в конечном числе точек.
Адитивность
интеграла. Пусть
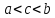 .
Тогда функция
.
Тогда функция интегрируема на отрезке
интегрируема на отрезке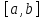 в том и только том случае, когда она
интегрируема на
в том и только том случае, когда она
интегрируема на и на
и на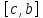 .
В этом случае
.
В этом случае
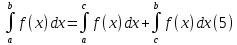
Если
точки
 расположены произвольно на числовой
прямой и каждый из интегралов в (5)
существует, то равенство (5) имеет место.
расположены произвольно на числовой
прямой и каждый из интегралов в (5)
существует, то равенство (5) имеет место.
Теорема 2. Кусочно-непрерывная функция интегрируема на любом отрезке.
Монотонность
интеграла.Если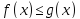 для всех
для всех и
и ,
то
,
то .
.
Как следующее свойство отметим одно простое равенство, вытекающее из определения определенного интеграла:
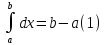
Оценка
интеграла.Если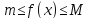 на отрезке
на отрезке и
и ,
то
,
то

Действительно,
 Здесь мы последовательно применили
монотонность интеграла, его линейность
и равенство (1). Аналогично доказывается
первое из неравенств в (2).
Здесь мы последовательно применили
монотонность интеграла, его линейность
и равенство (1). Аналогично доказывается
первое из неравенств в (2).
Например,
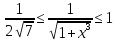 на отрезке
на отрезке ,
что следует из монотонности функции
,
что следует из монотонности функции а значит и функции
а значит и функции . Отсюда,
. Отсюда,
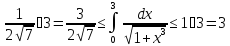
Теорема о среднем. Если функция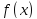 непрерывна на отрезке
непрерывна на отрезке ,
то найдётся точка
,
то найдётся точка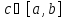 такая,
что
такая,
что
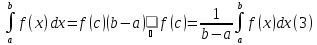
Величина
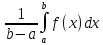 называется интегральным средним функции
называется интегральным средним функции на отрезке
на отрезке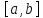 .
.
Пример. Пусть

Тогда
интегральное среднее функции (4) на
отрезке
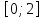 равно
равно

Однако
точки
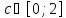 такой, что
такой, что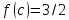 нет. Причина этого – разрыв функции
нет. Причина этого – разрыв функции в точке 1.
в точке 1.

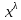 (λ ≠
0)
(λ ≠
0)
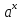
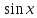
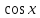

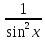

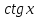
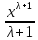
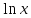

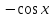
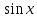

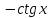
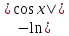

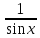


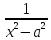
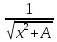

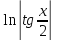


 (высокий
логарифм)
(высокий
логарифм) (длинный
логарифм)
(длинный
логарифм)