Контрольные вопросы

1. Какими соотношениями описывается поле электрического диполя?

2. Какие поля называются плоскомеридианными (осесимметричными)?

3. Какими соотношениями описывается поле бесконечно длинной заряженной оси?

§ 2.3. Электростатические поля простых двухпроводных линий Поле двух разноименно заряженных осей

Пусть в однородном диэлектрике находятся две параллельные бесконечно длинные оси, равномерно и разноименно заряженные с линейной плотностью заряда +и -(рис. 3). Изобразим на рисунке следы этих осей в плоскости поперечного сечения

Рис. 3.

Если принять , т.е. на оси симметрии. тоА =0. Теперь определим уравнение эквипотенциальных поверхностей. На этих поверхностях r₂/r₁=k = const. Здесь k – параметр семейства эквипотенциальных линий в плоскости рисунка.

Выразим r₂ и r₁ в декартовых координатах и выведем уравнение эквипотенциали в канонической форме относительно координат х и у

r₂ = ((x + a) ² + y ²)^0,5; r₁ = ((x – a) ² + y ²)^0,5

(x + a)² + y² = k ² (x – a)² + k ²y ²

(x + a)² – k ² (x – a)² + y²(1 – k ²)= 0

x²(1 – k ²) + 2ax(1 + k ²) + a²(1 – k ²) + y²(1 – k ²) = 0

x² + 2ax(1 + k ²)/(1 – k ²) + y² + a² = 0

(x + a(1 + k ²)/(1 – k ²))² + y² = (a(1 + k ²)/(1 – k ²))² – a² = (2ak/(1 – k ²))²

Здесь получено уравнение окружности в канонической форме:

(x – s)² + y² = R ² (1)

где s = a(k ²+1)/(k ²– 1) – координата центра окружности.

R = a|2k/(1 – k ²)| – радиус окружности.

Мы получили выражения для координаты центра и для радиуса эквипотенциальной линии по задаваемому параметру k, где .

В соответствии с уравнением (1) линии равного потенциала представляют собой окружности, а поверхности равного потенциала – круговые цилиндры, геометрические оси которых смещены относительно электрических осей. Одна из этих поверхностей вырождается в плоскость с нулевым значением потенциала (при k = 1: ;).

Линии напряженности представляют собой дуги окружности, начинающиеся на оси с положительным зарядом и кончающиеся на оси с отрицательным зарядом.

Если семейство равнопотенциальных поверхностей рассечь параллельными плоскостями, перпендикулярными заряженным осям, то в каждой плоскости получится одна и та же картина линий. Поля, обладающие таким свойством, называются плоскопараллельными (иначе их называют двумерными полями).

Установив картину поля и использовав следствие теоремы о единственности, можно считать решенными столько новых задач, сколько имеется различных по взаимному расположению пар равнопотенциальных поверхностей, которые можно рассматривать как поверхности проводников.

Рассмотрим важнейшие частные случаи таких задач.

Поле и емкость параллельных цилиндров с несовпадающими осями

Случай 1. «Коаксиальный» кабель со смещенной жилой.

Рис. 4.

Дано: R₁ – радиус жилы; R₂ – радиус оболочки; d – смещение осей жилы и оболочки; – напряжение между жилой и оболочкой (рис.4). Определить: емкость кабеля на единицу длины и потенциалы проводников относительно средней плоскости между электрическими осями.

из пояснений к уравнению (1) следует, что

(s – a)(s + a) = R²

(s + a)/R = R/(s – a) = k, если k > 1 (2)

Значит

s₂, s₁, a вычисляются из решения системы уравнений

; т. е.

;

Алгоритм вычислений: сначала рассчитываются s₂, s₁, a, затем C₀, потом .

Если нужно определить параметры эквипотенциали , то вычисляются величиныk_i, s_i, R_i, по формулам, дополняющим уравнение (1).

Пример расчёта электростатического поля и ёмкости «коаксиального» кабеля со смещённой жилой в ядре MATLAB и в PDE Toolbox дан на сайте по адресу http://www.matlab.ru/pde/book5/index.asp.

Здесь приведём тексты вычислительных сценариев расчёта электростатического поля коаксиального кабеля без и со смещением жилы.

% vannak - Расчёт электростатического полq в коаксиальном кабеле

%

% Входные данные: epsilon - проницаемость;

% rob - радиус оболочки; rz - радиус жилы;

% U - напрqжение; nf - число шагов по потенциалу.

%

% Выходные данные: c0 - ёмкость на единицу длины;

% rk - радиусы эквипотенциалей.

%

% В обычной фигуре строитсq картина эквипотенциалей

%

eps0=8.85419e-3; % Абсолютнаq диэлектрическаq проницаемость вакуума, пФ/мм

if exist('epsilon','var'), sepsilon=num2str(epsilon); else sepsilon='1'; end

if exist('rob','var'), srob=num2str(rob); else srob='250'; end

if exist('rz','var'), srz=num2str(rz); else srz='20'; end

if exist('U','var'), sU=num2str(U); else sU='10'; end

if exist('nf','var'), snf=num2str(nf); else snf='10'; end

SS=inputdlg({'epsilon','rob (миллиметры)','rz (миллиметры)','U (вольты)','nf шагов по потенциалу'},...

'Ввод исходных данных',1,{sepsilon,srob,srz,sU,snf});

epsilon=eval(SS{1}); rob=eval(SS{2}); rz=eval(SS{3}); U=eval(SS{4}); nf=eval(SS{5});

disp(['epsilon=',num2str(epsilon),'; rob=',num2str(rob),'; rz=',num2str(rz),'; U=',num2str(U),'; nf=',num2str(nf)])

c0=2*pi*eps0*epsilon/log(rob/rz)

fk=linspace(0,U,nf+1);

rk=rob*(rob/rz).^(-fk/U)

t=0:0.004*pi:2*pi;

for k=1:nf+1

plot(rk(k)*cos(t),rk(k)*sin(t),'k-')

hold on

end

grid on

% vannaks - Расчёт электростатического полq в "коаксиальном" кабеле со смещённой жилой

%

% Входные данные: epsilon - проницаемость;

% rob - радиус оболочки; rz - радиус жилы;

% d - смещение оси жилы относительно оси оболочки;

% U - напрqжение;

% nf - число шагов по потенциалу.

%

% Выходные данные: c0 - ёмкость на единицу длины;

% rk - радиусы эквипотенциалей.

%

% В обычной фигуре строитсq картина эквипотенциалей

%

eps0=8.85419e-3; % Абсолютнаq диэлектрическаq проницаемость вакуума, пФ/мм

if exist('epsilon','var'), sepsilon=num2str(epsilon); else sepsilon='1'; end

if exist('rob','var'), srob=num2str(rob); else srob='250'; end

if exist('rz','var'), srz=num2str(rz); else srz='20'; end

if exist('d','var'), sd=num2str(d); else sd='40'; end

if exist('U','var'), sU=num2str(U); else sU='10'; end

if exist('nf','var'), snf=num2str(nf); else snf='10'; end

SS=inputdlg({'epsilon','rob (миллиметры)','rz (миллиметры)','d (миллиметры)','U (вольты)','nf шагов по потенциалу'},...

'Ввод исходных данных',1,{sepsilon,srob,srz,sd,sU,snf});

epsilon=eval(SS{1}); rob=eval(SS{2}); rz=eval(SS{3}); d=eval(SS{4}); U=eval(SS{5}); nf=eval(SS{6});

disp(['epsilon=',num2str(epsilon),'; rob=',num2str(rob),'; rz=',num2str(rz),'; d=',num2str(d),'; U=',num2str(U),'; nf=',num2str(nf)])

s1=(rob^2-rz^2-d^2)/2/d;

s2=(rob^2-rz^2+d^2)/2/d;

a=sqrt(s1^2-rz^2);

c0=2*pi*eps0*epsilon/log((s2-a)*(s1+a)/rob/rz)

tau=c0*U;

fz=tau*log((s1+a)/rz)/(2*pi*eps0*epsilon);

fob=tau*log(rob/(s2-a))/(2*pi*eps0*epsilon);

fk=linspace(0,U,nf+1);

hi=((s2-a)*(s1+a)/rob/rz).^((fob+fk)/U);

x=s2-a*(hi.^2+1)./(hi.^2-1)

rk=2*a*abs(hi./(1-hi.^2))

t=0:0.004*pi:2*pi;

for k=1:nf+1

plot(rk(k)*cos(t)+x(k),rk(k)*sin(t),'k-')

hold on

end

grid on

Случай 2. Двухпроводная линия с проводами разного радиуса.

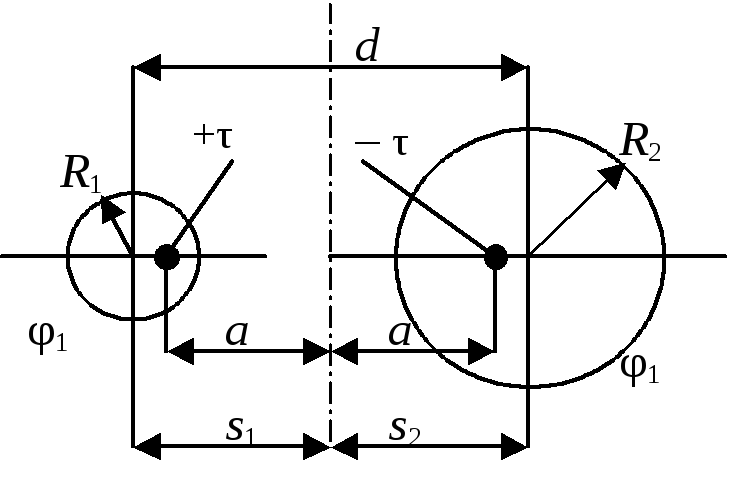
Рис. 5.

Дано: R₁ – радиус положительно заряженного провода; R₂ – радиус отрицательно заряженного провода; – напряжение между проводами;d – смещение осей цилиндрических проводов (рис. 5).

Определить: емкость линии на единицу длины и потенциалы проводников относительно средней плоскости между электрическими осями . Так же как и в предыдущем случае

Для s₁, а, R₁, k₁ справедливо соотношение (2), поскольку k> 1. Если k<1, то вместо (2) имеем

(s + a)/R = R/(s – a) = – k,

В это соотношение подставим s = – s₂, R = R₂, k = k₂,

(s₂ – a)/ R₂ = R₂/(s₂ + a) = k₂,

Значит,

s₂, s₁, a вычисляются из решения системы уравнений

; т. е.

;

Алгоритм вычислений тот же, что и в предыдущем случае.

В рассмотренных двух случаях результирующую напряженность электрического поля можно определить по формуле

.

Значения емкости на единицу длины C₀, полученные при решении этих задач, могут быть использованы при анализе работы линии при переменных токах и напряжениях.

Известно, что при наличии переменного магнитного поля электрическое напряжение между двумя точками зависит от формы пути, соединяющего эти точки. Однако в длинных линиях переменного тока линии магнитной индукции практически лежат в плоскостях поперечного сечения; контур, лежащий в этой плоскости, не пронизывается переменным магнитным потоком, поэтому циркуляция вектора E вдоль такого контура равна нулю, т.е. электрическое поле имеет потенциальный характер. Это и дает возможность говорить об однозначном мгновенном значении напряжения между точками двух проводников, лежащими в одной и той же плоскости поперечного сечения, и постоянстве отношения мгновенных значений , справедливом для любого поперечного сечения.