1. 2.10. Полная система уравнений Максвелла.

Полный анализ макроскопических электромагнитных процессов возможен на основе полной системы основных уравнений электродинамики. К числу которых относят:

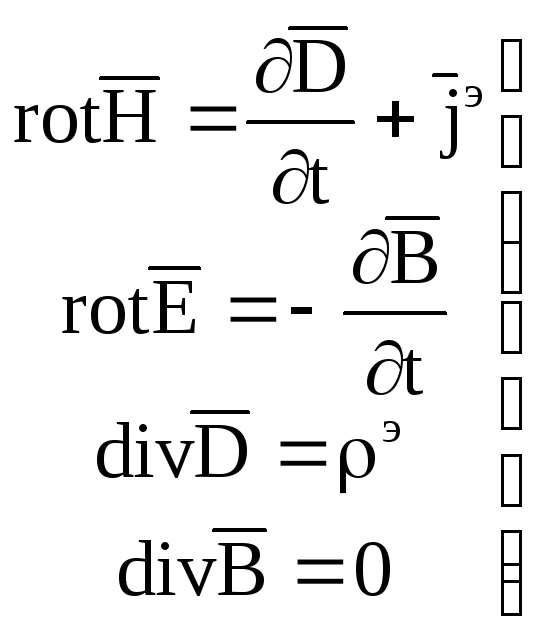- 4 уравнения Максвелла (2)

-система уравнений состояний (материальные уравнения) (3)

Для линейных анизотропных сред уравнения Максвелла остаются в той же самой форме, а в уравнениях состояния хотя бы один электродинамический параметр (_а, _а, ) является тензорной величиной.

На основе уравнений Максвелла можно сделать заключение о свойствах электромагнитного поля:

1. Электрическое и магнитное поля взаимосвязаны. Независимое существование электрического поля возможно только в электростатическом случае.

2. Источником электромагнитного поля являются электрические заряды и токи.

3. магнитное поле всегда вихревое, электрическое поле может быть как вихревым, так и потенциальным. Чисто потенциальное электрическое поле возможно только в электростатическом случае.

4. Силовые линии электрического поля могут иметь исток, сток. Силовые линии магнитного поля всегда непрерывны.

5. Из первого уравнения Максвелла следует, что соленоидальное магнитное поле охватывает силовые линии полного тока, образуя с ними правовинтовую систему.

6. Из 2 уравнения Максвелла следует, что линии вихревого электрического поля охватывают силовые линии вектора 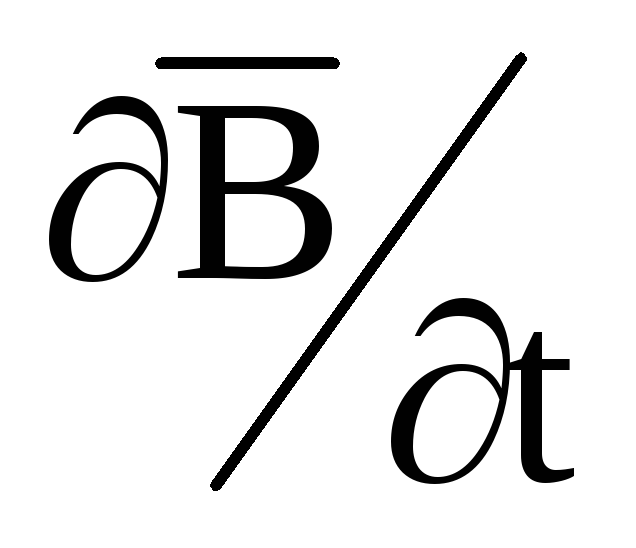, образуя с ними левовинтовую систему.

7. Уравнения Максвелла являются линейными и дифференциальными, поэтому для электромагнитного поля справедлив принцип суперпозиции, т.е. поле, создаваемое системой источников электромагнитного поля, можно определить как сумму полей, создаваемых отдельными источниками.

8. при рассмотрении электродинамических задач используют уравнения Максвелла в интегральной форме.

Магнитный поток во втором уравнении Максвелла считается положительным или отрицательным в зависимости от того совпадает или нет с положительной единичной нормалью поверхности. В свою очередь векторное полесчитается положительным или отрицательным в зависимости от того происходит увеличение или уменьшение положительного магнитного потока.

Уравнения образующие полную систему электродинамики являются линейными дифференциальными уравнениями. Поэтому можно утверждать, что для электромагнитных полей справедлив принцип суперпозиции: поле возбужденное системой источников можно представить как сумму полей отдельных источников. В ряде случаев уравнения Максвелла в дифференциальной форме оказываются не применимы. В этих задачах мы используем уравнения Максвелла в интегральной форме.

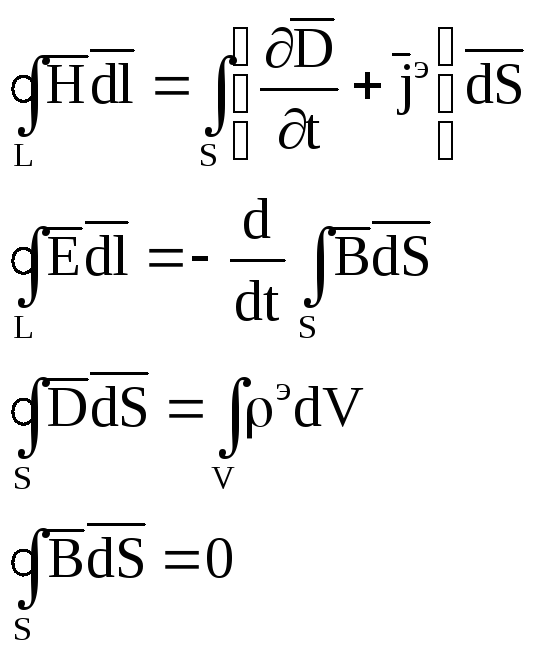
В случае гармонических электромагнитных полей систему уравнений Максвелла можно упростить, используя искусственный прием: метод комплексных амплитуд.

2. 2.11 Классификация электромагнитных сред.

Совокупность уравнений Максвелла и материальных уравнений позволяют рассмотреть любые электромагнитные процессы классической электродинамики. В ряде случаев эти уравнения могут быть упрощены.

1 случай. Пусть, электромагнитное поле не зависит от времени и отсутствует перемещение заряженных частиц. В этом случае полная система распадается на две не связанные системы (1) и (2). Таким образом, в этом случае электрические и магнитные поля можно считать независимыми.

; ;(1)

; ;(2).

Верхняя система (1) описывает поле неподвижных, неизменных во времени электрических зарядов (электростатические задачи). Она называется полной системой дифференциальных уравнений электростатики. Нижняя система (2) описывает магнитное поле постоянных магнитов. С ее помощью может быть решена задача о магнитном поле, возбуждаемом постоянными токами, которыепротекают вне рассматриваемой области, которая не «сцеплена» с линиями тока (не охватывает линиями тока). Подобные задачи называются магнитостатическими, а систему называют полной системой дифференциальных уравнений магнитостатики.

Если в рассматриваемой области присутствуют постоянные токи, то магнитное и электрическое поля нельзя считать независимыми. В этом случае полная система уравнений электродинамики записывается в следующем виде: ,,,,,,:система (3).

Электромагнитное поле постоянных токов называется стационарным, а систему (3)называют полной системой дифференциальных уравнений стационарного электромагнитного процесса.

В случае стационарного процесса электрическое и магнитное поля взаимосвязаны. Иногда в отдельную группу выделяют квазистационарные процессы (медленно меняющиеся во времени).

В этом случае, если в рассматриваемой области:

в квазистационарных процессах .

В случае гармонических процессов решение электродинамических задач упрощается путем использования теории ФКП (введение комплексных амплитуд).