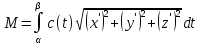LEKTsII / Тема 12 ПриложениеИнтеграла
.docxПриложение определённого интеграла
Оглавление
1Площадь плоской фигуры 1
2Полярные координаты 2
2.1Площадь криволинейного сектора 3
3Объём тела 4
4 Длина дуги 5
5Площадь поверхности 7
6Приложение определённого интеграла к вычислению физических величин 8
6.1Длина пути 8
6.2Работа силы 8
6.3Центр тяжести 9
6.4Момент инерции 10
6.5Масса тяжелой нити 11
-
Площадь плоской фигуры
Пусть
криволинейная трапеция задана так:
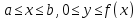 с непрерывной неотрицательной функцией
с непрерывной неотрицательной функцией
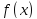 .
Тогда площадь S этой криволинейной
трапеции равна
.
Тогда площадь S этой криволинейной
трапеции равна
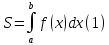
Пусть теперь
криволинейная трапеция задана так:
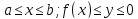 с
непрерывной функцией
с
непрерывной функцией
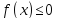 .
Тогда площадь S этой криволинейной
трапеции равна
.
Тогда площадь S этой криволинейной
трапеции равна
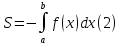
Рассмотрим
теперь криволинейную трапецию
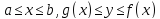 с непрерывными функциями f(x) и g(x) такими,
что
с непрерывными функциями f(x) и g(x) такими,
что
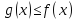 для любой точки
для любой точки
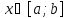 .
Тогда площадь S этой криволинейной
трапеции равна
.
Тогда площадь S этой криволинейной
трапеции равна
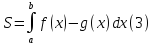
Пример.
Вычислим площадь
 фигуры
ограниченной графиками
фигуры
ограниченной графиками

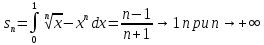
Пусть
функция задана параметрически
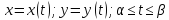 при чем функция
при чем функция
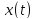 биективна, а
биективна, а
 .
Тогда площадь под графиком равна
.
Тогда площадь под графиком равна
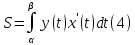
Пример. Вычислим площадь под первой аркой циклоиды
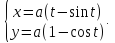
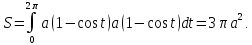
-
Полярные координаты
Пусть P --
точка на декартовой плоскости
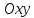 .
Обозначим через r=r(P) расстояние от P до
начала координат и назовём это число
полярным радиусом. Через 𝜑
=𝜑 (P) обозначим
угол, на который надо повернуть ось
.
Обозначим через r=r(P) расстояние от P до
начала координат и назовём это число
полярным радиусом. Через 𝜑
=𝜑 (P) обозначим
угол, на который надо повернуть ось
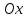 до совмещения с направлением вектора
до совмещения с направлением вектора
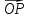 ;
эту величину назовём полярным углом.
Полярный угол не определен для начала
координат. Пара
;
эту величину назовём полярным углом.
Полярный угол не определен для начала
координат. Пара
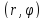 называется полярными координатами
точки P. Ясно, что
называется полярными координатами
точки P. Ясно, что
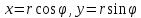 ,
,
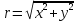 ,
,
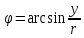 ,
если
,
если
 и
и

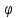
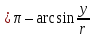 ,
если
,
если
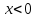
Пример.
Нарисуем кривую
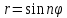 для n=1, 2,3,4.
для n=1, 2,3,4.
n=1
–
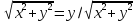 ⇔
⇔
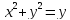 -- окружность радиуса 1/2 с центом в точке
(0;1/2)
-- окружность радиуса 1/2 с центом в точке
(0;1/2)
n=2
– восьмерка. Декартова запись
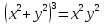
n=3 – трилистник.
n=4 -- “четырехлистник»
-
Площадь криволинейного сектора
Обозначим через K криволинейный сектор -- фигуру на плоскости, заданную системой неравенств
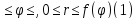
( -- непрерывная функция.) Найдём площадь
S(K) этого
сектора. Для этого обозначим через S(τ
) площадь сектора заданного также как
и в (1), но с =τ. Тогда
-- непрерывная функция.) Найдём площадь
S(K) этого
сектора. Для этого обозначим через S(τ
) площадь сектора заданного также как
и в (1), но с =τ. Тогда
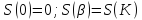 .
Придадим приращение
.
Придадим приращение
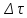 переменной
переменной
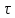 .
Линеаризуем (найдем дифференциал)
приращения
.
Линеаризуем (найдем дифференциал)
приращения
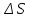 ,
заменив узкий криволинейный сектор на
круговой сектор с углом
,
заменив узкий криволинейный сектор на
круговой сектор с углом
 и радиусом
и радиусом
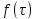 .
Его площадь равна
.
Его площадь равна
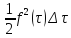 ,
-- линейная функция относительно
,
-- линейная функция относительно
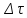 .
Следовательно,
.
Следовательно,
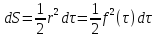
Отсюда
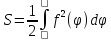
Примеры.
Площадь лепестка трилистника
 .
.
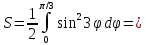
Площадь,
ограниченную лемнискатой
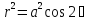 .
.
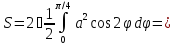
Площадь,
ограниченную кардиоидой
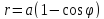
-
Объём тела
Пусть в
пространстве задано тело V и ось Ox; причём
тело расположено в полосе a≤ x≤ b.
Предположим, что известна площадь
сечения тела плоскостью
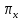 перпендикулярной оси Ox и проходящей
через точку x. Обозначим эту площадь
S(x). Обозначим через V(x) объем левой части
тела V, отсекаемого плоскостью
перпендикулярной оси Ox и проходящей
через точку x. Обозначим эту площадь
S(x). Обозначим через V(x) объем левой части
тела V, отсекаемого плоскостью
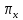 .
Тогда Δ V -- объем слоя от
x до
.
Тогда Δ V -- объем слоя от
x до
 Отсюда
Отсюда
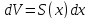 .
Значит
.
Значит
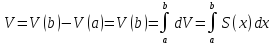
Следствие (принцин Кавальери) Если два тела имеют одинаковые площади сечения на одинаковой высоте, то объёмы этих тел совпадают.
В частности,
если V -- тело вращения, т.е. получено
вращением криволинейной трапеции
 ,
то сечение
,
то сечение
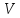 плоскостью, проходящей через x и
параллельной координатной плоскости
OYZ есть круг радиуса
плоскостью, проходящей через x и
параллельной координатной плоскости
OYZ есть круг радиуса
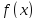 .
Следовательно, S(x)=π f(x)2 в этом
случае и объём тела вращения
.
Следовательно, S(x)=π f(x)2 в этом
случае и объём тела вращения
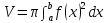
Определенную
выше криволинейную трапецию F можно
вращать и относительно оси Oy. При этом
надо наложить дополнительное условие
0≤ a. Обозначим через V(x) объём вращения
вокруг оси Oy части этой трапеции
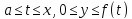 .
Тогда dV можно представлять как площадь
кольца с внутренним радиусом x, толщиной
dx и высотой равной f(x). Тем самым
.
Тогда dV можно представлять как площадь
кольца с внутренним радиусом x, толщиной
dx и высотой равной f(x). Тем самым
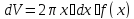 Отсюда получаем, что объём тела вращения
вокруг оси Oy равен
Отсюда получаем, что объём тела вращения
вокруг оси Oy равен
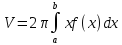
Примеры
1. Объём шара радиус R.
Шар представляем как тело вращения
полукруга -R≤ x≤ R;
 вокруг оси Ox. Тогда
вокруг оси Ox. Тогда
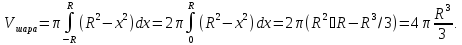
Пример
2. Объём "обобщенного конуса" с
площадью основания S и высоты H. Пусть
вершина конуса имеет координату 0, а
основание имеет координату H. Обозначим
площадь сечения плоскостью
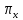 через
через
 .
Тогда
.
Тогда
 ,
откуда
,
откуда
 .
Следовательно,
.
Следовательно,
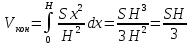
3. Объём обобщённого цилиндра с площадью основания S и высоты H. В обозначениях предыдущего примера имеем S(x)=S. Отсюда
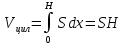
-
Длина дуги
Кривой γ в пространстве называется отображение
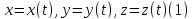
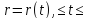 .
Здесь t называется параметром. Точка
.
Здесь t называется параметром. Точка
 называется началом кривой γ , а точка
называется началом кривой γ , а точка
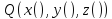 называется концом. Если P=Q, то кривая
γ называется замкнутой. Кривая γ
называется непрерывной, если функции
называется концом. Если P=Q, то кривая
γ называется замкнутой. Кривая γ
называется непрерывной, если функции
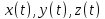 непрерывны. Кривая называется гладкой,
если существуют непрерывные производные
непрерывны. Кривая называется гладкой,
если существуют непрерывные производные
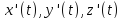 ,
причём они не равны нулю одновременно.
Кривая γ называется кусочно-гладкой,
если её можно разбить на конечное число
гладких кусков.
,
причём они не равны нулю одновременно.
Кривая γ называется кусочно-гладкой,
если её можно разбить на конечное число
гладких кусков.
Примеры. 1. Отрезок прямой
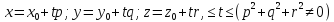
2. Окружность
 .
Считая а)
.
Считая а)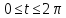 , б)
, б)
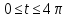 , в)
, в)
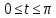 получим разные кривые.
получим разные кривые.
3. Винтовая линия радиуса R и с шагом H
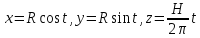
4. Цепная
линия - график функции
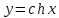 .
.
5. Периметр квадрата - пример кусочно гладкой, но не гладкой кривой
Длина
кривой. Пусть
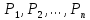 -- точки пространства. Тогда кривую
-- точки пространства. Тогда кривую

назовём
ломаной, а число
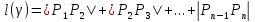 назовём длиной этой ломаной. Пусть (1)
-- произвольная кривая, и
назовём длиной этой ломаной. Пусть (1)
-- произвольная кривая, и
 -- разбиение. Обозначим
-- разбиение. Обозначим
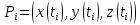 .
Тогда ломаную
.
Тогда ломаную
 назовём вписанной в
назовём вписанной в
 .
Длиной кривой
.
Длиной кривой
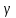 называется предел длин вписанных
ломаных, если максимум длин звеньев
стремиться к 0.
называется предел длин вписанных
ломаных, если максимум длин звеньев
стремиться к 0.
Теорема.
Пусть
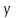 -- кусочно-гладкая кривая. Тогда
-- кусочно-гладкая кривая. Тогда
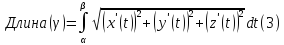
Доказательство.
Обозначим через
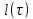 -- длину кривой (1) с отрезком изменения
параметра от до
τ. Тогда
-- длину кривой (1) с отрезком изменения
параметра от до
τ. Тогда
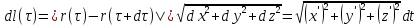
Отсюда следует результат. ??? –более точное док-во
Следствие.
Если
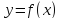 -- дифференцируемая функция с кусочно
непрерывной производной на отрезке
-- дифференцируемая функция с кусочно
непрерывной производной на отрезке
 ,
то длина дуги графика этой функции на
данном отрезке будет равна
,
то длина дуги графика этой функции на
данном отрезке будет равна

Примеры. 1. Длина отрезка PQ равна

 2.
Длина окружности
2.
Длина окружности
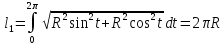
3. Длина одного витка винтовой линии
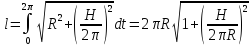
4. Длина цепной линии
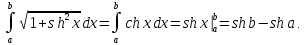
-
Площадь поверхности
Площадь
поверхности, полученной вращением
графика функции
 (при условии
(при условии
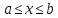 )
вокруг оси Ох равна
)
вокруг оси Ох равна
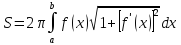
-
Приложение определённого интеграла к вычислению физических величин
-
Длина пути
Тело движется
по прямой Ox с известной скоростью
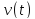 .
Известно положение тела в начальный
момент времени:
.
Известно положение тела в начальный
момент времени: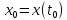 .
Где будет находится тело в момент
.
Где будет находится тело в момент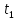 ?
?
Ответ:
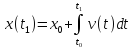
Это следствие
формулы Ньютона-Лейбница и того факта,
что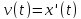 .
Аналогично, если известна зависимость
ускорения от времени --
.
Аналогично, если известна зависимость
ускорения от времени --
 ,
то
,
то

Пример
равноускоренного движения. Пусть
ускорение постоянно и равно
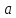 ,
а тело в начальный момент времени
,
а тело в начальный момент времени
 находилось в начале координат
находилось в начале координат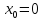 и имело нулевую скорость
и имело нулевую скорость
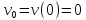 .
Тогда
.
Тогда
 ,
,
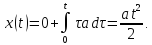
-
Работа силы
Пусть тело
движется по оси Ox и в каждой точке
 известна проекция силы, действующей на
это тело, на ось --
известна проекция силы, действующей на
это тело, на ось --
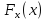 .
Тогда работа силы при перемещении из
точки a в точку b равна
.
Тогда работа силы при перемещении из
точки a в точку b равна
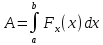
Пример.
Сила действующая на пружину растянутую
на x относительно положения равновесия
равна
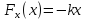 .
Отсюда работа этой силы будет
.
Отсюда работа этой силы будет
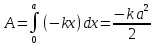
-
Центр тяжести
Пусть в
пространстве задана система точечных
масс
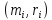 (1≤
i≤ n). Тогда,
по определению, центр тяжести данной
системы -- это точка
(1≤
i≤ n). Тогда,
по определению, центр тяжести данной
системы -- это точка
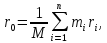
где
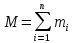 -- масса всей системы.
-- масса всей системы.
Пусть теперь задана однородная плоская пластинка
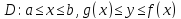
Найдём
центр тяжести этой пластинки. Для этого
разобьём пластинку D на полоски прямыми
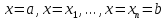 .
Каждую полоску аппроксимируем
прямоугольником
.
Каждую полоску аппроксимируем
прямоугольником
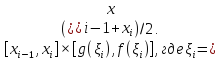
Её центр
тяжести находится в точке
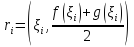 ,
а масса равна
,
а масса равна
 .
Заменим всю пластинку на систему точечных
масс
.
Заменим всю пластинку на систему точечных
масс
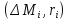 .
Тогда приближённо центр тяжести пластинки
равен
.
Тогда приближённо центр тяжести пластинки
равен
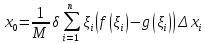

где -- масса пластинки,
-- масса пластинки,
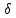 -- поверхностная плотность, а
-- поверхностная плотность, а
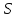 -- площадь пластинки. Переходя к пределу
-- площадь пластинки. Переходя к пределу
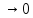 ,
и сокращая на
,
и сокращая на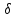 ,
получим окончательную формулу
,
получим окончательную формулу
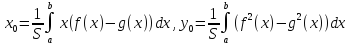
где
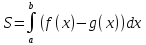 .
.
-
Момент инерции
Пусть
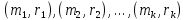 -- система точечных масс. Моментом
инерции этой системы относительно
точки P (прямой ℓ , плоскости π ) называется
число
-- система точечных масс. Моментом
инерции этой системы относительно
точки P (прямой ℓ , плоскости π ) называется
число
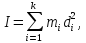
где
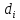 -- расстояние от i-ой точки до точки P
(прямой ℓ , плоскости π ).
-- расстояние от i-ой точки до точки P
(прямой ℓ , плоскости π ).
Момент
инерции однородного цилиндра относительно
своей оси. Обозначим R -- радиус цилиндра,
H -- высоту цилиндра, c -- плотность.
Обозначим также через
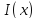 ,
(
,
(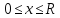 )
момент инерции такого же цилиндра, но
радиуса
)
момент инерции такого же цилиндра, но
радиуса
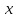 .
Тогда
.
Тогда
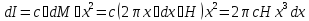
Отсюда
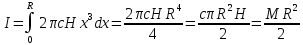 .
Здесь M -- масса цилиндра.
.
Здесь M -- масса цилиндра.
Момент
инерции однородного шара относительно
оси, проходящей через центр. Пусть R
-- радиус шара. Ось Ox проходит через центр
шара. Пусть
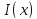 (
(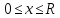 )
-- момент инерции части шара, состоящей
из точек, удаленных от начала координат
на расстояние
)
-- момент инерции части шара, состоящей
из точек, удаленных от начала координат
на расстояние
 относительно начала координат. Тогда
относительно начала координат. Тогда

Отсюда
 где M -- масса шара.
где M -- масса шара.
Заметим,
что (
(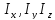 -- моменты инерции оносительно координатных
осей). В нашем случае
-- моменты инерции оносительно координатных
осей). В нашем случае
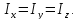 Отсюда
Отсюда
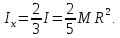
-
Масса тяжелой нити
Пусть
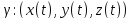 ,
≤
t ≤
-- кусочно гладкая кривая, описывающая
форму нити с линейной плотностью c(t).
Тогда масса нити вычисляется по формуле
,
≤
t ≤
-- кусочно гладкая кривая, описывающая
форму нити с линейной плотностью c(t).
Тогда масса нити вычисляется по формуле