6. Определители

Пусть --n×n–матрица над полем К.Определителем матрицыA называется элемент поля K , который вычисляется по следующему правилу

Теорема 1. Определитель -- полилинейная и кососимметричная функция строк матрицы.

Доказательство. Из определения определителя вытекает, что

где не зависят от первой строки. В силу предложения, получаем линейность по первой строке. Аналогично доказывается линейность по остальным строкам.

Далее, пусть в матрице мы переставили t -ую и s -ую строку и получили матрицу. В этой матрице

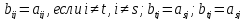
Обозначим через τ транспозицию (ts) . Без ограничения общности можно считать, что t<s . Тогда

что и требовалось доказать. Здесь учтено, что при умножении на транспозицию четность подстановки меняется. □

Теорема 2.Определитель треугольной матрицы равен произведению элементов на главной диагонали. В частности, det E=1 .

Доказательство.Пусть -- верхнетреугольная n×n -матрица. Тогда произведение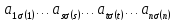равно 0, если хотя бы для одного i имеет место неравенство σ(i)<i . рассмотрим оставшийся случай: для любого i выполнено неравенство σ(i)≥ i . Тогда σ(n)=n ; далее σ(n-1)=n-1 и т.д. вплоть до σ(1)=1 . Итак, в оставшемся случае имеется только одна подстановка -- единичная. Тогда. В точности такая же формула имеет место и для нижнетреугольной матрицы. Доказательство аналогично.□

Теорема 3. Любая полилинейная и кососимметричная функцияпропорциональна определителю, а именно𝒟(A)=𝒟(E)⋅det A для любой квадратной матрицы A . Если, кроме того,𝒟(E)=1 , то𝒟(A)= det A для любой матрицы A .

Доказательство. Рассмотрим n×n -матрицы , у которых на месте (i,j) стоит 1, а на остальных местах стоят нули. Тогда произвольная n×n-матрицаможет быть записана так: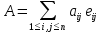. Пользуясь полилинейностью, получаем равенство

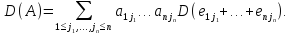
Но , если найдутся индексыi≠i' такие, что(см. свойство после определения кососимметричности). Если же индексывсе различны, то

,

как следует из кососимметричности. Обозначив подстановку через σ, мы приходим к равенству

Отсюда и следует утверждение теоремы. □

Отметим теперь некоторые свойства определителей

Свойство A.Определитель матрицы равен определителю транспонированной матрицы.

Доказательство. Действительно, для любой подстановки σ , как следует из теоремы о том, что четность подстановки определяется четностью числа транспозиций, в которые она раскладывается (см. ???). Пусть матрицаполучается из n×n-матрицыAтранспонированием. Тогда

□

В силу равенства все свойства, доказанные для строк, автоматически переносятся на столбцы и наоборот. В частности

Свойство Б.Определитель -- полилинейная и кососимметричная функция столбцов матрицы.

Свойство В.Определитель равен нулю, если какие-либо две строки (два столбца) совпадают.

Это свойство мы отмечали ранее в более общем случае для полилинейной функции. Следующее свойство также следствие полилинейности.

Свойство Г.Определитель с нулевой строкой (столбцом) равен нулю.

Свойство Д.Определитель не изменится, если над строками (столбцами) совершить элементарное преобразование первого типа, т.е. к одной строке прибавить другую, умноженную на какое-либо число

Доказательство. Это утверждение -- следствие полилинейности и свойства 3:

F(… a+ b… b… )=F(… a… b… )+ F(… b… b… )=F(… a… b… )

Здесь F -- любая полилинейная и кососимметричная функция строк. □

Определение. (i,j) -ым минором матрицы A называется определитель матрицы, получающейся из A вычеркиванием i -ой строки и j -го столбца. Обозначается этот минор --. Алгебраическим дополнением (i,j) –го элемента матрицы A называется величина.

Свойство Е.Разложение определителя по j -му столбцу и i -ой строке:

Доказательство. Функция полилинейна и кососимметрична. Кроме того, легко вычислить, что𝒟(E)=1 . Остается применить теорему единственности.□

Имеют место также ложные разложения по r -ой строке и r -ому столбцу; если и, то

Действительно, правая часть здесь совпадает с определителем матрицы, у которой две строки (два столбца) совпадают.