4. Матричное исчисление

Матрицей размера или–матрицей называется прямоугольная таблица вида⋮

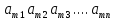
мыслимая как единый математический объект. Матрицы будем обозначать прописными латинскими буквами -- A,B,Cи т.д. Более компактная запись матрицы (1) следующая:. Очень часто ссылку "" на размер матрицы A будем опускать, записывая ее короче:. Две матрицы равны, если, во-первых, совпадают их размеры, а во-вторых, на одинаковых местах стоят равные друг другу числа. Матрицы

;

называются i- ой строкой иj- ым столбцом матрицы.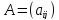

Матрица, у которой число строк и столбцов совпадают, называется квадратной. Элементы 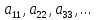называются главной диагональю матрицы.

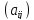Матрица A называется верхнетреугольной, если ниже главной диагонали матрицы A стоят нули. Аналогично, A - нижнетреугольная матрица, если выше главной диагонали матрицы A стоят нули. Матрица A треугольная, если она либо верхнетреугольная, либо нижнетреугольная. Треугольная матрица с нулями на главной диагонали называется строго треугольной.

Матрицы можно складывать поэлементно, если они имеет одинаковый размер, а также поэлементно можно умножать матрицу слева и справа на число. Иными словами,

Транспонирование матрицы -- операция над -матрицей A , превращающая ее в–матрицу, у которой-ый коэффициент равен-ому коэффициенту матрицы A . Свойства операции транспонирования следующие:

Т1. ;

Т2. ;

Т3. ;

1. Произведение матриц

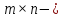Произведение строки на столбецтого размера определяется как число – матрица 1х1 равная. Произведениемматрицынаматрицуназываетсяматрицатакая, что

Теорема. Произведение матриц ассоциативно.

Единичная матрица есть квадратная матрица, у которой на главной диагонали единицы, а остальные все коэффициенты 0,

Предложение.Единичная матрица -- нейтральный элемент по отношению к произведению матриц, то естьдля любойматрицыA.

Докажем это предложение, записав - коэффициент единичной матрицы как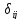. По определению

, еслии равно 0, если

Таким образом, определенная величина называется символом Кронекера.

Относительно транспонирования произведение матриц обладает следующим свойством

Т4. .

5. Подстановки

Подстановкой на 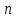символах называется ряд чиселзаписанный в каком-либо порядке. Обозначим подстановку. Здесьи все-ые попарно различны.

Пару подстановкиназываем инверсией, если, но. Подстановканазывается четной, если количество всех инверсий у нее четно (записываемназывается нечетной, если количество всех инверсий у нее нечетно (записываем. Величину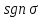называют также знаком подстановки.

Теорема.Перестановка местами двух чиселв подстановкеменяет ее знак на противоположный.

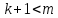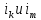Доказательство. Это ясно, если . Если же, то перестановкуможно осуществить сдвигая последовательновправораз, покане займет позицию сразу после, а затемсдвигаем влевораз, покане займет -ую позицию. Итого мы совершимнечетное число танспозиций меняющих два соседних элемента. При каждой такой транспозиции подстановка меняет знак. Следовательно, в итоге подстановка изменит знак.□

Семейство всех подстановок обозначим . Ихштук, половина из которых четные, а половина – нечетные.

Для подстановки будем также придерживаться обозначения.