
LEKTsII / Тема 10 Неопределенный интеграл
.docxНеопределенный интеграл
Оглавление
1Первообразная и неопределенный интеграл 1
2Простейшие свойства неопределенного интеграла. 3
Таблица основных интегралов 3
2.1Дополнительная таблица интегралов 4
3Замена переменной в неопределённом интеграле 5
3.1Метод интегрирования функций вида и (a≠ 0). 6
4Интегрирование по частям в неопределённом интеграле 7
4.1Метод интегрирования функций вида . 7
4.2Метод интегрирования функций вида : 8
5Интегрирование рациональных дробей 8
5.1Метод интегрирования простейших дробей 4 типа. 11
6Интегрирование иррациональных выражений 12
6.1Интегрирование тригонометрических выражений 14
-
Первообразная и неопределенный интеграл
Решаем дифференциальное уравнение

на интервале
 ,
т.е. находим такую функцию
,
т.е. находим такую функцию
 ,
что
,
что
 .
Так как
.
Так как
 ,
то уравнение (1) можно переписать в
дифференциалах:
,
то уравнение (1) можно переписать в
дифференциалах:

Любое
решение такого уравнения называется
первообразной функции
 .
Итак, функция
.
Итак, функция
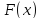 называется первообразной функции
называется первообразной функции
 на интервале
на интервале
 ,
если
,
если
 для всех
для всех
 .
Случаи
.
Случаи
 и/или
и/или
 не исключаются. Ясно, что если
не исключаются. Ясно, что если
 первообразная, то и
первообразная, то и
 также первообразная. Наша задача –
найти все решения уравнения (1). Функция
двух переменных
также первообразная. Наша задача –
найти все решения уравнения (1). Функция
двух переменных
 называется общим решением уравнения
(1) или, по-другому, неопределенным
интегралом функции
называется общим решением уравнения
(1) или, по-другому, неопределенным
интегралом функции
 ,
если при подстановке вместо
,
если при подстановке вместо
 любого числа получаем частное решение
уравнения (1) и любое частное решение
уравнения (1) получается таким образом.
любого числа получаем частное решение
уравнения (1) и любое частное решение
уравнения (1) получается таким образом.
Неопределённый
интеграл обозначается
 .
Функция
.
Функция
 называется подинтегральной, дифференциал
называется подинтегральной, дифференциал
 называется подинтегральным выражением,
а
называется подинтегральным выражением,
а
 -- знак интеграла (растянутая латинская
буква S, первая буква слова
Sum – сумма). Возникает
вопрос о существовании первообразной
и неопределенного интеграла. В разделе
«Определенный интеграл», §
Формула Ньютона-Лейбница будет доказано,
что первообразная непрерывной функции
всегда существует.
-- знак интеграла (растянутая латинская
буква S, первая буква слова
Sum – сумма). Возникает
вопрос о существовании первообразной
и неопределенного интеграла. В разделе
«Определенный интеграл», §
Формула Ньютона-Лейбница будет доказано,
что первообразная непрерывной функции
всегда существует.
Лемма.
Пусть
 тождественно для всех
тождественно для всех
 .
Тогда
.
Тогда
 -- константа на этом интервале.
-- константа на этом интервале.
Доказательство.
Обозначим
 для какой-либо точки
для какой-либо точки
 .
Возьмём произвольную точку
.
Возьмём произвольную точку
 и к разности
и к разности
 применим теорему Лагранжа:
применим теорему Лагранжа:
 для некоторой точки
для некоторой точки
 .
Отсюда
.
Отсюда
 и лемма доказана.□
и лемма доказана.□
Теорема о первообразных. Две первообразных одной и той же функции, определенной на интервале, отличаются на константу.
Доказательство.
Пусть
 и
и
 -- первообразные функции
-- первообразные функции
 .
Тогда
.
Тогда
 откуда, по лемме
откуда, по лемме
 -- константа. Следовательно,
-- константа. Следовательно,
 .
□
.
□
Следствие.
Если
 -- первообразная функции
-- первообразная функции
 ,
то
,
то
 .
.
Заметим,
что если в качестве ОДЗ функции взять
не интервал, а, например, такое несвязное
множество как объединение двух интервалов
 ,
то любая функция вида
,
то любая функция вида

имеет нулевую производную, и тем самым лемма и теорема о первообразных перестает быть верной в этом случае.
-
Простейшие свойства неопределенного интеграла.
1. Интеграл от суммы равен сумме интегралов:

2. Константу можно выносить за знак интеграла:

3. Производная от интеграла равна подинтегральной функции.
4. Дифференциал от интеграла равен подинтегральному выражению.
5. (Линейная
замена переменных) Если
 ,
то
,
то
 (здесь
(здесь
 ).
).
Таблица основных интегралов

В частности,

Для
исключительного случая
 имеем:
имеем:

Далее









-
Дополнительная таблица интегралов









-
Замена переменной в неопределённом интеграле
Определение
неопределенного интеграла распространим
на более общий случай: полагаем по
определению
 .
Таким образом, например
.
Таким образом, например
 .
.
Теорема.
Пусть
 -- дифференцируемая функция. Тогда
-- дифференцируемая функция. Тогда

Доказательство.
Пусть
 .
Тогда
.
Тогда

что и требовалось доказать.□
В частном
случае, когда
 получаем линейную замену переменных
(см. свойство 5, §1).
Применение формулы (1) "слева на право"
и будет означать замену переменной .
Применение формулы (1) в обратном
направлении, "справа налево"
называется занесением под знак
дифференциала.
получаем линейную замену переменных
(см. свойство 5, §1).
Применение формулы (1) "слева на право"
и будет означать замену переменной .
Применение формулы (1) в обратном
направлении, "справа налево"
называется занесением под знак
дифференциала.
Примеры.
А.


-
Метод интегрирования функций вида
 и
и
 (a≠ 0).
(a≠ 0).
1. Выделяем в числителе производную квадратного трехчлена:

2. Тогда

3. Для вычисления первого интеграла в (2) применяем занесение под знак дифференциала:

Для вычисления второго интеграла выделяем в квадратном трехчлене полный квадрат и линейной заменой переменных сводим его к табличному.
Таким же
методом вычисляются и интегралы вида

Примеры
В.

Г.

-
Интегрирование по частям в неопределённом интеграле
Теорема.
Для дифференцируемых функций
 и
и
 имеет место соотношение
имеет место соотношение

Доказательство.
Интегрируя левую и правую часть формулы
 ,
получаем:
,
получаем:

Так как по
определению
 и
и
 ,
то формула (1) следует.□
,
то формула (1) следует.□
Пример.

-
Метод интегрирования функций вида
 .
.
Здесь и
далее
 – многочлен степени n. Метод интегрирования
состоит в занесении экспоненты или
гармоники под знак дифференциала, а
затем применяется формула интегрирования
по частям. Повторяем эту процедуру n
раз.
– многочлен степени n. Метод интегрирования
состоит в занесении экспоненты или
гармоники под знак дифференциала, а
затем применяется формула интегрирования
по частям. Повторяем эту процедуру n
раз.
Пример.

-
Метод интегрирования функций вида
 :
:
Для интегрирования таких функций заносим многочлен под знак дифференциала и применяем формулу интегрирования по частям. Процедуру повторяем k раз.
Пример.


-
Интегрирование рациональных дробей
Рациональной
дробью называется функция вида
 ,
где
,
где
 – многочлены. Если
– многочлены. Если
 ,
то рациональную дробь
,
то рациональную дробь
 называют правильной. В противном
случае ее называют неправильной.
называют правильной. В противном
случае ее называют неправильной.
Следующие рациональные дроби называют простейшими
(1 тип)
 ,
,

(2 тип)


(3 тип)


(4 тип)
 ,
,

Теорема 1. Любую дробь можно разложить в сумму многочлена и правильной рациональной дроби.
Доказательство.
Пусть
 – неправильная рациональная дробь.
Поделим числитель на знаменатель с
остатком:
– неправильная рациональная дробь.
Поделим числитель на знаменатель с
остатком:
 Здесь
Здесь
 --
многочлены, причем
--
многочлены, причем
 Тогда
Тогда

Дробь
 правильная в силу неравенства
правильная в силу неравенства
 . □
. □
Теорема 2. Любую правильную рациональную дробь можно разложить в сумму простейших.
Алгоритм разложения.
а) Знаменатель
правильной дроби
 раскладываем в произведение неприводимых
многочленов (линейных и квадратичных
с отрицательным дискриминантом):
раскладываем в произведение неприводимых
многочленов (линейных и квадратичных
с отрицательным дискриминантом):

Здесь
 и
и
 -- кратности соответствующих корней.
-- кратности соответствующих корней.
б) Раскладываем
дробь
 в сумму простейших с неопределенными
коэффициентами по следующим принципам:
в сумму простейших с неопределенными
коэффициентами по следующим принципам:
-
множителю
 соответствует k простейших дробей
первого и второго типов с неопределенными
коэффициентами в числителе:
соответствует k простейших дробей
первого и второго типов с неопределенными
коэффициентами в числителе:

-
множителю
 соответствует m простейших дробей
третьего и четвертого типов:
соответствует m простейших дробей
третьего и четвертого типов:

Так мы поступаем для каждого линейного множителя и для каждого квадратичного множителя.
в) Получившееся
разложение умножаем на общий знаменатель
 ,
и неопределенные коэффициенты отыскиваем
из условия тождественности левой и
правой части. Действуем комбинацией
двух методов
,
и неопределенные коэффициенты отыскиваем
из условия тождественности левой и
правой части. Действуем комбинацией
двух методов
-
в получившееся равенство подставляем вместо
 корни знаменателя
корни знаменателя
 как действительные так и комплексные;
как действительные так и комплексные; -
в получившемся равенстве приравниваем коэффициенты при одинаковых степенях
??? – обоснование алгоритма
Примеры.
А. Разложим
 в сумму простейших
в сумму простейших

Отсюда
следует, что
 .
Подставляя в это соотношение
.
Подставляя в это соотношение
 находим сразу
находим сразу
 .
Итак
.
Итак

Б. Разложим
рациональную дробь
 в сумму простейших. Разложение этой
дроби с неопределенными коэффициентами
имеет вид
в сумму простейших. Разложение этой
дроби с неопределенными коэффициентами
имеет вид

Умножая на общий знаменатель, получаем соотношение

Подставляя
сюда
 ,
находим
,
находим
 ,
откуда
,
откуда
 .
Подставляя
.
Подставляя
 находим
находим
 .
Приравнивая коэффициенты при
.
Приравнивая коэффициенты при
 получаем систему
получаем систему
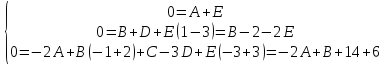
Отсюда
 и
и
 .
Складывая равенства последней системы,
получаем
.
Складывая равенства последней системы,
получаем
 и
и
 .
Тогда
.
Тогда
 и
и

Следовательно,

/**/ Задача. Обобщить результат примера А и доказать равенство

-
Метод интегрирования простейших дробей 4 типа.
а) Выделяя
в числителе производную знаменателя,
разложим интеграл
 в сумму двух интегралов.
в сумму двух интегралов.
б) Первый из получившихся интегралов, после занесения под знак дифференциала, станет табличным.
в) Во втором
в знаменателе выделяем полный квадрат
и сводим вычисление к интегралу вида
 .
К этому интегралу применяем следующую
рекуррентную процедуру
.
К этому интегралу применяем следующую
рекуррентную процедуру

К последнему интегралу применяем формулу интегрирования по частям:

Итак, если
обозначить
 ,
то
,
то



Это
представляет собой рекуррентную формулу
вычисления интегралов
 c учетом начального
значения
c учетом начального
значения
 .
.
Пример


-
Интегрирование иррациональных выражений
Далее
 -- рациональная функция одной или
нескольких переменных.
-- рациональная функция одной или
нескольких переменных.
Интегралы
вида
 ,
где m/n,...,r/s -- рациональные числа с общим
знаменателем k, сводятся к интегралу
от рациональной функции заменой
,
где m/n,...,r/s -- рациональные числа с общим
знаменателем k, сводятся к интегралу
от рациональной функции заменой

Тогда
 суть рациональные выражения, следовательно,
после подстановки, получается интеграл
от рациональной дроби:
суть рациональные выражения, следовательно,
после подстановки, получается интеграл
от рациональной дроби:

Вычислив
этот интеграл (см. пар. 4) и сделав обратную
замену
 ,
получим ответ.
,
получим ответ.
Аналогично, интегралы вида

где ad-bc≠ 0, а k имеет тот же смысл как и выше, сводятся к интегралам от рациональной дроби заменой
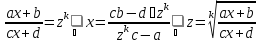
Примеры. А. Вычислим интеграл

Б. Вычислим интеграл

Более простой метод интегрирования (но требующий догадки) этой же функции таков:

-
Интегрирование тригонометрических выражений
Интегралы
вида
 сводятся к интегралам от рациональной
функции универсальной заменой
сводятся к интегралам от рациональной
функции универсальной заменой

Тогда


поэтому получаем интеграл от рационального выражения
В частных
случаях R(sin x) cos x
dx,
R(cos x)
sin x dx
и R(sin2x, cos2x,
tg x, ctg x) dx лучше пользоваться заменами
 соответственно.
соответственно.
Примеры. А.

Б.

