4 Параллельные алгоритмы в задачах сортировки

Сортировка - одна из самых частых операций, выполняемых компьютером. Поскольку сортированными данными проще манипулировать, множество алгоритмов требуют уже отсортированных данных. Сортировка имеет дополнительное значение в параллельных вычислениях из-за её близости к задаче распределения данных среди процессоров, которая является основной частью многих параллельных алгоритмов. Большое количество параллельно сортирующих алгоритмов было исследовано для множества параллельных архитектур вычислительных систем. Эта глава представляет несколько параллельно сортирующих алгоритмов для таких архитектур, как гиперкуб, параллельные компьютеры с общей и распределенной памятью.

Сортировка определяется как задача размещения неупорядоченного набора элементов монотонно по возрастанию (или убыванию) порядка. Допустим S = (a¹, a², ..., aⁿ) - последовательность из n элементов заданных в произвольном порядке; сортируя S монотонно по возрастанию получим последовательность S' - {a'₁, a'₂, ..., a'_n} таким образом, что a'_i ≤ a'_j для 1 ≤ i ≤ j ≤ n, и S' является перестановкой S.

Сортирующие алгоритмы разделяются на внутренние и внешние. Во внутренней сортировке ряд элементов, который будет отсортирован, является достаточно небольшим, чтобы разместиться в оперативной памяти. Напротив, внешние сортировочные алгоритмы используют вспомогательную память (такую как жесткие диски) для того, чтобы сортировать, потому что ряд элементов, который будет отсортирован, является слишком большим, чтобы разместиться одновременно в памяти. Эта глава концентрируется только на внутренних сортировочных алгоритмах.

Сортирующие алгоритмы могут быть выделены как основанные на сравнении и основанные на несравнении. Основанный на сравнении алгоритм сортирует неупорядоченную последовательность элементов, неоднократно сравнивая пары элементов и, если они не в том порядке, заменяя их. Эту фундаментальную операцию, основанную на сравнении, называют сравнение и обмен. Нижняя граница на последовательной сложности любого основанного на сравнении сортировочного алгоритма - Θ (n log n), где n - ряд элементов сортировки. Основанные на несравнении алгоритмы сортируют при использовании определенных известных свойств элементов (таких как их двоичное представление или их распределение). В основном упор будет сделан на алгоритмах основанных на сравнении.

4.1 Проблемы сортировки на вычислительных машинах параллельного действия

Параллелизование последовательного сортировочного алгоритма возводит в степень распространение элементов, которые будут сортированы на доступные процессоры. Этот процесс проявляет многие проблемы, к которым мы должны обратиться, чтобы более качественно отобразить параллельные сортирующие алгоритмы.

В последовательных сортировочных алгоритмах входные и сортированные последовательности хранятся в памяти процессора. Однако, в параллельной сортировке есть два варианта, где эти последовательности могут находится. Они могут быть сохранены только на одном из процессоров, или они могут быть распространены среди процессоров. Последний подход особенно полезен, если сортировка - промежуточный шаг в другой алгоритм. В этой главе мы предполагаем, что входные и сортированные последовательности распространены среди процессоров.

Теперь рассмотрим точное распределение сортированной последовательности результата среди процессоров. Общий метод распределения должен перечислить процессоры и использовать это перечисление, чтобы определить распределение глобальной переменной сортированной последовательности. Другими словами, последовательность будет сортирована относительно этого перечисления процессоров. Например, если Pi, прибывает прежде, чем Pj в перечислении, все элементы, сохраненные в Pi, будет меньше чем сохраненные в Pj. Мы можем перечислить процессоры разными способами. Для определенных параллельных алгоритмов и сетей соединения, некоторые перечисления приводят к более эффективным результатам чем другие.

Как выполняются сравнения. Последовательно сортирующий алгоритм может легко выполнить операции сравнивания и замены на двух элементах, потому что они сохранены локально в памяти процессора. В параллельно сортирующих алгоритмах этот шаг не настолько прост. Если элементы постоянно находятся на том же самом процессоре, сравнение может быть сделано легко. Но если элементы постоянно находятся на различных процессорах, местоположение становится более сложным.

Рисунок 4.1. Пример операции сравнения и обмена.

Процессоры P_i и P_j передают свои элементы друг другу. Процессор P_i сохраняет значение min{a_i,a_j}, а процессор P_j сохраняет значение max{a_i,a_j}.

4.1.1 Один элемент на один процессор. Рассмотрим случай, в котором каждый процессор хранит только один элемент последовательности, которая будет сортирована. В некоторый момент выполнения алгоритма, пара процессоров (P_i, P_j) должна сравнить их элементы, a_i и a_j. После сравнения, P_i будет содержать меньшее значение, а P_j большее из {a_i, a_j}. Мы можем выполнить сравнение если оба процессора посылают их элементы друг другу. Каждый процессор сравнивает полученный элемент с его собственным и сохраняет соответствующий элемент. В нашем примере, P_i сохранит меньшее, а P_j сохранит больший из {a_i, a_j}. Как в последовательном случае, мы обращаемся к операциям сравнение - замена. Как показано на иллюстрации 6.1, каждая операция требует одного шага сравнения и одного шага коммуникации.

Если мы предполагаем, что процессоры P_i и P_j являются соседями и каналы коммуникации двунаправлены, то затраты на коммуникации сравнения – обмена будут равны времени (t_s + t_w), где t_s и t_w - время старта сообщения и время передачи слова, соответственно. В коммерчески доступных компьютерах t_s значительно больше чем t_w. Надо заметить, что в сегодняшних вычислительных машинах параллельного действия пересылка одного элемента от одного процессора до другого занимает больше времени чем непосредственно сравнение. Следовательно, любая параллельно сортирующая система которая использует столько же процессоров сколько и сортируемых элементов будет иметь очень малую производительность за счет того, что время вычислений на процессорах будет ничтожно меньше времени межпроцессорной коммуникации.

4.1.2 Больше чем один элемент на процессор. Универсальный параллельно сортирующий алгоритм должен быть способен сортировать большую последовательность с помощью относительно небольшого количества процессоров. Пусть p будет количеством процессоров P₀, P₁,..., P_p-1, и пусть n - количество сортируемых элементов. Каждому процессору назначают блок n/p элементов, и все процессоры сотрудничают, чтобы отсортировать последовательность. Пусть A₀, A₁, ... , A_p-1 будут блоки направляемые на процессоры P₀, P₁, ... , P_p-1 соответственно. Мы говорим, что A_i ≤ A_j, если каждый элемент A_i меньше чем каждый элемент в A_j. Когда сортировочный алгоритм заканчивает свою работу, каждый процессор P_i хранит множество A_i` таким образом, что A<sub>i</sub>` ≤ A_j` для i ≤ j и .

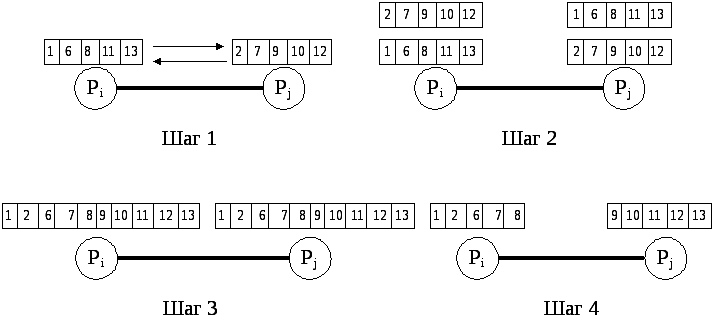
Рисунок 4.2. Операция сравнения-разбиения

На рисунке 4.2. каждый процессор посылает свой блок размера n/p на другой процессор. Каждый процессор объединяет полученный блок с его собственным блоком и сохраняет только соответствующую половину объединенного блока. В этом примере процессор Pi сохраняет меньшие элементы, а процессор Pj, сохраняет большие элементы. Как и в случае "один элемент на процессор", двум процессорам P_i и P_j, вероятно, придется перераспределить свои блоки элементов n/p так, чтобы один из них получил меньшие n/p элементы, а другой, большие n/p элементы. Пусть A_i и A_j будут блоками, сохраненными в процессорах P_i и P_j. Если блок n/p элементов в каждом процессоре уже сортирован, перераспределение может быть сделано эффективно следующим образом. Каждый процессор посылает свой блок в другой процессор. Дальше каждый процессор объединяет два сортированных блока и сохраняет только соответствующую половину объединенного блока. Назовем операции сравнения и разбивания двух сортированных блоков как сравнение-разбиение. Операция сравнения-разбиения поясняется на рисунке 4.2. Если мы предполагаем, что процессоры P_i и P_j - соседи и что каналы коммуникации двунаправлены, то затраты на коммуникации операции сравнения-разбиения будут равны (t_s+t_wn/p). Поскольку увеличивается размер блока, роль времени t_s уменьшается, и для достаточно больших блоков оно может игнорироваться. Таким образом, время, требуемое объединить два сортированных блока n/p элементов равно Θ (n/p).

4.1.3 Сортирующие сети. В поисках быстрых сортирующих методов, было спроектировано много различных сетей для сортировки n элементов, со временем значительно меньшим чем Θ(n log n). Эти сортировочные сети основаны на модели сети сравнения, в которой много операций сравнения выполняемых одновременно.

Ключевой компонент этих сетей - компаратор. Компаратор - устройство с двумя входами x и y и двумя выходами x' и y'. Для увеличивающего компаратора, x' = min {x, y}, а y' = max {x, y}; для уменьшающего компаратора x' = max {x, y}, а y' = min {x, y}. Рисунок 4.3 дает схематическое представление двух типов компараторов.

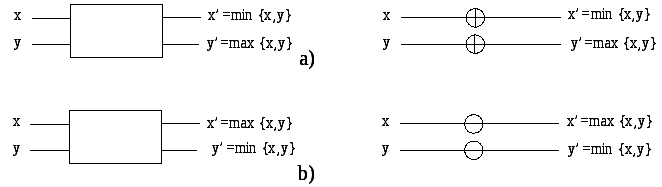
Рисунок 4.3. Схематическое представление компараторов: (a) увеличивающий компаратор, и (b) уменьшающий компаратор.

Два элемента поступают на входы компаратора, сравниваются и, в случае необходимости, меняются прежде, чем они пойдут на выход. Обозначим увеличивающий компаратор Θ , а уменьшающий компаратор Ө. Сортировочная сеть обычно составляется из последовательности столбцов, и каждый столбец содержит множество компараторов, подключенных в параллель. Каждый столбец компараторов выполняет перестановку, и результат, полученный из конечного столбца, сортирован по увеличению или уменьшению порядка. Рисунок 4.4 поясняет типичную сортировочную сеть. Глубина сети - количество столбцов, которые она содержит. Так как скорость компаратора – технологически зависимая константа, скорость сети - пропорциональна его глубине.

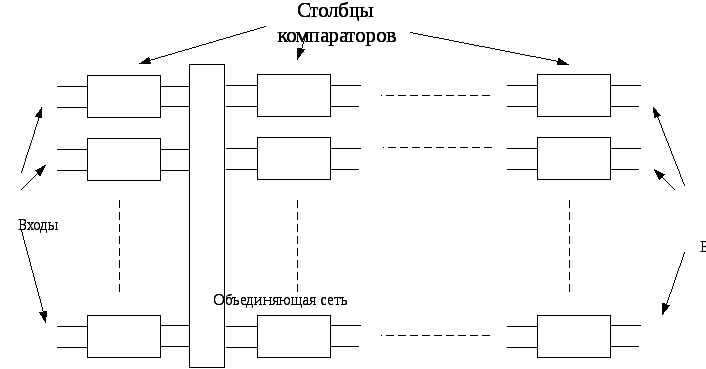
Рисунок 4.3. Типичная объединяющая сортировочная сеть.

Каждая сортировочная сеть составлена из набора столбцов. Каждый столбец содержит несколько компараторов, подключенных в параллель.

Можно преобразовать любую сортировочную сеть в последовательный сортировочный алгоритм, подражая компараторам в программном обеспечении и выполняя сравнения каждого столбца последовательно. Компаратор эмулируется операцией сравнения-обмена, где x и y сравниваются и, в случае необходимости, меняются.

4.1.4 Сортировка битоник. Битоник сеть представляет сортировочную сеть, которая сортирует n элементов за время Θ (log² n). Чтобы упростить понимание мы возьмем n равной степени двойки.

Ключевая операция битоник сортировочной сети является перестановкой битоник последовательности в сортированную последовательность. битоник последовательность - последовательность элементов {a₀, a₁, …, a_n-1}, при условии (1), что существует такой индекс i, 0 ≤ i ≤ n - 1, при котором последовательность {a₀,..., a_i} монотонно увеличивается, а последовательность {a_i,…,a_n-1} монотонно уменьшается, или (2), там существует циклический сдвиг индексов так, чтобы удовлетворялось условие (1). Например, {1, 2, 4, 7, 6, 0} битоник последовательность, потому что она сначала увеличивается, а затем уменьшается. Точно так же {8, 9, 2, 1, 0, 4} тоже битоник последовательность, потому что это - циклический сдвиг {0, 4, 8, 9, 2, 1}.

Рассмотрим методику, перестройки битоник последовательности, для получения монотонно увеличивающейся последовательности. Пусть s = {a₀, a₁, …, a_n-1} будет битоник последовательностью таким образом, что a₀ ≤ a₁ ≤ ...≤ a_n/2-1 и a_n/2 ≥ a_n/2+1 ≥ … ≥ a_n-1. Рассмотрим следующие подпоследовательности s:

s1 = {min [a₀,a_n/2], min[a₁,a_n/2+1], …, min[a_n/2-1,a_n-1]},

s2 = {max [a₀,a_n/2], max[a₁,a_n/2+1], …, max[a_n/2-1,a_n-1]} (4.1)

В последовательности s₁ существует элемент b_i = min [a_i, a_n/2+i] такой, что все элементы до b_i из увеличивающейся части исходной последовательности, а все элементы после b_i из уменьшающейся части. Аналогично в последовательности s2 существует элемент b_i = max [a_i, a_n/2+i] такой, что все элементы до b_i из уменьшающейся части исходной последовательности, а все элементы после b_i из увеличивающейся части. Таким образом, можно сказать, что s1 и s2 – битоник последовательности. Кроме того, каждый элемент первой последовательности меньше чем каждый элемент второй последовательности. b_i больше или равен любого элемент из s_i, b_i’ меньше или равен любого элемента из s₂, и b_i^’ больше или эквивалентно b_i. Таким образом, мы упростили начальную задачу перестановки битоник последовательности размерности n. Остается отсортировать две меньшие последовательности и их объединить. Мы должны использовать операцию разбивания битоник последовательности размера n на две битоник последовательности, определенные Уравнением 6.1 как битоник разбиение. Хотя при получении s₁ и s₂ мы предполагали, что у первоначальной последовательности были увеличивающая и убывающая последовательности одинаковой длины, операция битоник разбиения проводится для любой битоник последовательности.

Можно рекурсивно получить более короткие битоник последовательности, используя Уравнение 6.1 для каждой из битоник последовательностей, пока не достигнем последовательности из одного элемента. В таком случае результат уже будет сортирован в увеличивающемся порядке монотонно. Так как после каждого битоник разбиения, размер задачи делится на два, количество разбиений, требуемых для перестановки битоник последовательность в отсортированную последовательность, является логарифмом n. Процедура сортировки битоник последовательности использующая разбиения битоник называется слиянием битоник. Рекурсивная процедура слияния битоник поясняется на рисунке 4.5.

Оригинальная последовательность	3	5	8	9	10	12	14	20	95	90	60	40	35	23	18	0
Разделение 1	3	5	8	9	10	12	14	0	95	90	60	40	35	23	18	20
Разделение 2	3	5	8	0	10	12	14	9	35	23	18	20	95	90	60	40
Разделение 3	3	0	8	5	10	9	14	12	18	20	35	23	60	40	95	90
Разделение 4	0	3	5	8	9	10	12	14	18	20	23	35	40	60	90	95

Рисунок 4.5. Слияние bitonic последовательности с 16 элементами из серии log 16 разбиений bitonic.

Этот метод легко осуществить на сети компараторов. Такая сеть компараторов, известных как объединяющая сеть битоник, показана на рисунке 4.6. Сеть содержит log n столбцов. Каждый столбец содержит n/2 компараторов и выполняет один шаг слияния битоник. Эта сеть берет на вход битоник последовательность и подает на выход последовательность в сортированном порядке. Обозначим битоник сеть с n входами как ΘBM [n]. Если мы заменим компараторы рисунка 4.6 на уменьшающие компараторы, то входные данные будут отсортированы в порядке уменьшения монотонно; такую сеть обозначим ӨBM [n].

Вооружившись битоник сетью, рассмотрим подходы решения задачи сортировки n неупорядоченных элементов. Это можно осуществить, неоднократно объединяя битоник последовательности, как показано на рисунке 4.7.

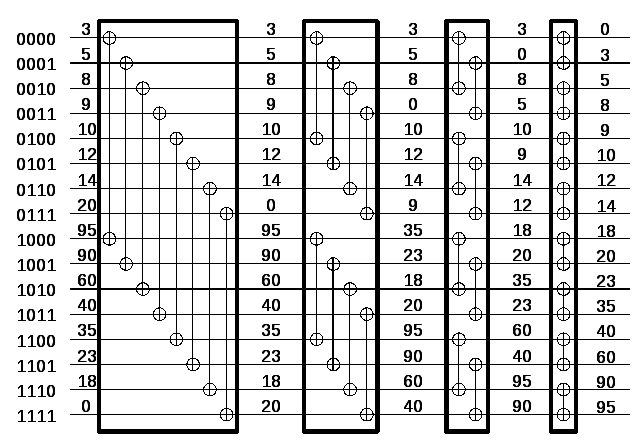
Рисунок 4.6 Битоник объединяющая сеть для n = 16.

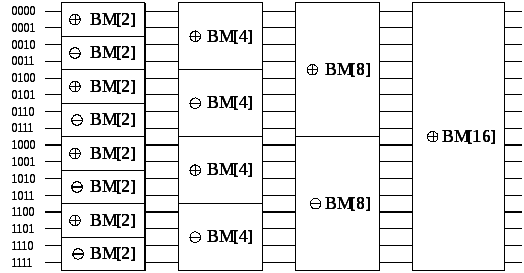
Рисунок 4.7 Схематичное представление сети преобразующей входную последовательность в битоник последовательность.

Как этот метод работает. Последовательность двух элементов x и y формирует битоник последовательность, или вида x ≤ y, когда у битоник последовательности есть x и y в увеличивающейся части и никаких элементов в уменьшающейся части, или вида x ≥ y, когда у битоник последовательности есть x и y в уменьшающейся части и никаких элементов в увеличивающейся части. Следовательно, любая несортированная последовательность элементов - конкатенация битоник последовательностей из двух элементов. Каждая стадия сети, которая показана на рисунке 4.7, объединяет смежный канал битоник последовательности в увеличении и уменьшении порядка. Согласно определению битоник, последовательность, полученная, связывая увеличивающую и убывающую последовательности, является битоник. Следовательно, результат каждой стадии в сети на рисунке 4.7 - конкатенация битоник последовательностей, которые являются в два раза длиннее, чем на входе. Объединяя всё большие и большие битоник последовательности, мы в конечном счете получаем битоник последовательность размера n. Объединение этой последовательности сортирует исходные данные. Назовем алгоритм, воплощенный в этом методе как битоник сортировка, а сеть как битоник сортирующая сеть. Первые три стадии сети на рисунке 4.7 показаны более наглядно на рисунке 4.8. Последняя стадия рисунка 4.7 показана наглядно на рисунке 4.6.

Последняя стадия битоник сортировочной сети последовательности из n элементов содержит битоник объединяющую сеть с n входами. Глубина log n. Другие стадии выполняют полную сортировку n/2 элементов. Следовательно, глубина, d (n), показанная на рисунке 4.7 получается из следующего рекуррентного соотношения:

d(n) = d(n/2)+log(n) (6.2)

Решая выражение 6.2, получим следующее выражение:

.

Такая сеть может быть реализована на последовательных компьютерах. Битоник сортирующая сеть может быть очень легко адаптирована и реализована на параллельных компьютерах, в том числе гиперкубе, с распределенной и общей памятью.

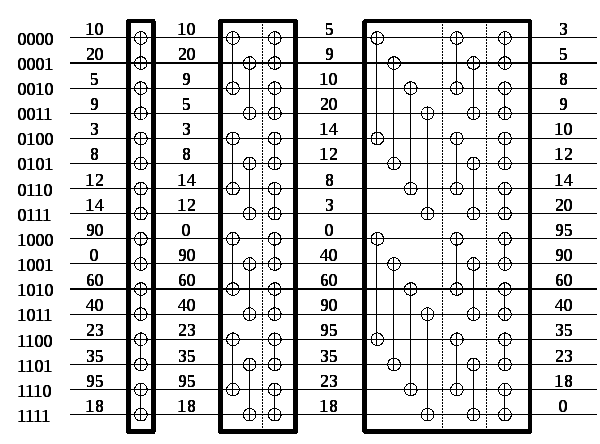
Рисунок 4.8 Сеть компараторов, которая преобразует входную последовательность из 16 несортированных данных в битоник последовательность.