2. Взаимосвязь структур алгоритмов и исполнителей

Понятие связанности алгоритма. Алгоритмы различаются связанностью выполняемых операций. Рассмотрим для наглядности пример вычисления суммы S восьми чисел, предложенный в [4]

S=a₁+ a₂+ a₃+a₄+ a₅+a₆+ a₇+ a₈. (2.1)

Это вычисление можно выполнить по двум алгоритмам, соответствующим следующим математически эквивалентным формулам:

S=((((((a₁ + a₂) + a₃) + a₄) + a₅) + a₆) + a₇) + a₈, (2.2)

S=((a₁ + a₂)+(a₃ + a₄))+((a₅ + a₆)+(a₇ + a₈)). (2.3)

В обоих случаях требуется выполнить 7 сложений. Поэтому с точки зрения времени вычисления сумм на последовательном компьютере существенного различия между этими алгоритмами нет. Различие заключается в количестве обращений к оперативной памяти, определяемых приоритетом выполнения операций сложения, согласно представленных скобочных форм записи. В выражении (2.2) их - 8, в (2.3) – 14.

В алгоритме (2.2) никакие операции нельзя выполнять независимо. Каждое следующее вычисление можно выполнить только, если будут выполнены последовательно друг за другом все предыдущие. Вначале вычисляется (a₁+ a₂), затем + a₃ и последним действием выполняется + a₈ . Такие алгоритмы называются связанными, или сильносвязанными.

В алгоритме (2.3) на первом шаге можно одновременно выполнить 4 независимых между собой сложений: b₁= (a₁ + a₂), b₂= (a₃ + a₄), b₃= (a₅ + a₆) и b₄= (a₇ + a₈). На втором шаге можно выполнить 2 независимых сложения: c₁=(b₁ + b₂) и c₂=(b₃ + b₄). И, наконец, на третьем шаге за 1 сложение заканчивается вычисление всей суммы S = (c₁ + c₂). Алгоритмы, в которых отдельные вычисления не зависят от других вычислений, называются слабосвязанными.

Алгоритмы, в которых все вычисления можно выполнить независимо друг от друга называются несвязанными.

Сильносвязанным алгоритмам соответствует многостадийная, или конвейерная структура исполнителя. В конвейерной структуре каждой операции соответствует исполнитель своего уровня, или стадии. Выполнение алгоритма заключается в последовательном выполнении каждой операции на своей стадии с последующей передачей результата вычисления на следующую. После загрузки исполнителей соответствующих всем стадиям конвейерной обработки, получение каждого следующего результата вычисления сильносвязанного алгоритма будет соответствовать времени работы одного исполнителя (цикл выполнения операции).

Для несвязанных алгоритмов наилучшее быстродействие достигается, использованием многоэлементной обработки, или параллельной структуры исполнителя. В параллельной структуре каждому процессору соответствует своя операция несвязанного алгоритма, выполняемая на одном шаге. Следовательно, все операции алгоритма будут выполнены за один такт процессора параллельной вычислительной системы.

Степень связанности алгоритмов порождает множество структур исполнителей, органически согласованных с алгоритмами вычислений.

Рассмотрим две задачи: вычисление некоторой функции y = f(x), с помощью аппроксимирующего степенного полинома

y = a_n*xⁿ + a_n-1*x^n-1 + … + a_1*x + a₀ (2.4)

и вычисление произведения n*n-матриц C = AB.

Если представить полином (2.4) в виде схемы Горнера

y = (…(a_n*x + a_n-1) _* x + … + a₁) _* x + a₀,

то полученное математическое выражение представляет собой не что иное, как сильносвязанный алгоритм вычисления полинома (18) путем n последовательных повторений выполнения однотипных операций

a^*_i-1 = (a_i*x + a_i-1). (2.5)

Структурная схема исполнителя, реализующего конвейер этих операций представлена на рисунке 2.1.

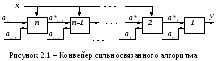
Следовательно, время получения решений функции (2.3) после загрузки всех n исполнителей конвейера, как следует из (1.12), будет равно T_t, где T_t – время выполнения операции (2.4).

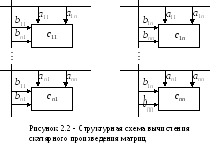
Во второй задаче в терминах скалярных произведений каждый элемент матрицы С вычисляется как скалярное произведение:

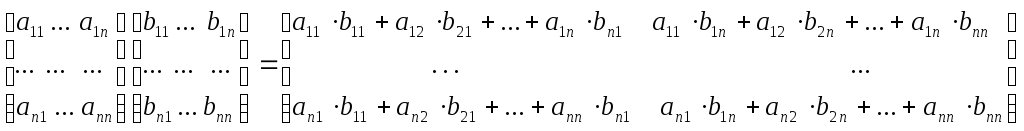, (20)

. (2.6)

Для ее решения в однопроцессорной ЭВМ необходимо выполнить n² однотипных процедур вычисления суммы произведений (2.6). Учитывая, что вычисление каждого элемента матрицы не зависит друг от друга, можно, используя многоэлементную (параллельную) обработку, сократить время решения задачи вn² раз, доведя его до времени вычисления процедуры (2.6).

На рисунке 2.2 показана структурная схема ядра параллельной системы вычисления скалярного произведения матриц, согласно выражению (2.5).