5.6.4 Задание № 4

Цель: Исследование характеристик ЦИС. Исследование влияния шага интегрирования h на погрешность для формул численного интегрированияm = 0 и m = 1 . Оценка влияния величины трансформированной погрешности и погрешности квантования на результат решения.

Порядок выполнения

Используя модель параллельной ЦИС, полученной при выполнении задания № 2, провести исследования зависимости погрешности решения СУШ на выбранном интервале вычисления функции, от изменения шага интегрирования для частных формул численного интегрирования: m = 0 и m = 1. Исследования проводятся путем расчета и построения на ЭВМ графиков погрешности решения СУШ на интервале от шага интегрированияh для m = 0 и m = 1. Определить границы и степень влияния шага интегрирования на методическую погрешность вычисления, как составляющей общей погрешности решения. Сделать выводы по каждому проведенному исследованию.

Содержание отчета

В отчете должны быть приведены все полученные по результатам проведенных исследований графики погрешностей и обоснованные выводы.

Контрольные вопросы

1. Во сколько раз должна измениться величина методической погрешности формулы численного интегрирования при увеличении (уменьшении) шага интегрирования в четыре раза для формул прямоугольников, трапеций, парабол (квадратичных, кубичных)?

2. В каком случае уменьшение шага интегрирования уменьшает погрешность вычисления в ЦИС?

3. Какие составляющие общей погрешности вычисления зависят от шага интегрирования?

4. Что эффективнее по затратам оборудования в вашем варианте для уменьшения времени решения на интервале с заданной погрешностью: использовать более простую формулу численного интегрирования при малом шаге интегрирования или формулу высокого порядка при большем шаге интегрирования?

5.7 Примеры выполнения заданий

5.7.1 Моделирования функции , с использованием методов цис

Система уравнений Шеннона, согласно изложенной методики, представлена в таблице 5.7.

Таблица 5.7 –Преобразование функции к порождающей системе дифференциальных уравнений К.Шеннона

Подстановка	СУШ
; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; .	1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) ; 9) .

Структурная схема параллельной ЦИС, воспроизводящая функцию в соответствии с СУШ, представленной в таблице 5.7, показана на рисунке 5.4

Рисунок 5.4 -Структурная схема параллельной ЦИС воспроизводящая функцию

Составляем разностную схему СУШ на основе первых разностей и ранжируем уравнения СУШ:

Для решения воспользуемся интерполяционными формулами численного интегрирования по Стилтьесу:

а) На основе формулы прямоугольников:

б) На основе формулы трапеций:

Для вычисления значения нам неизвестно значение, а для вычислениянеизвестно значение.

Вычисление неизвестных значений приращений переменных выполняется методом экстраполяции. Порядок используемых в вычислении формул экстраполяции должен быть таким, чтобы замена приращений их экстраполированными значениями не привела бы к ухудшению методической погрешности. Это достигается когда порядок формулы экстраполяции на единицу выше порядка формулы численного интегрирования. Так как для формулы трапеции порядок погрешности , будем использовать формулу экстраполяции с порядком погрешности:

Отсюда, система уравнений К.Шеннона приобретает вид:

Вычислим значение шага интегрирования. Для этого воспользуемся формулой: , где

- шаг интегрирования,

- относительная погрешность,

- известные коэффициенты,

- максимальная циклическая частота - f=sup|f_{э max}|.

В варианте задания использованы следующие данные:

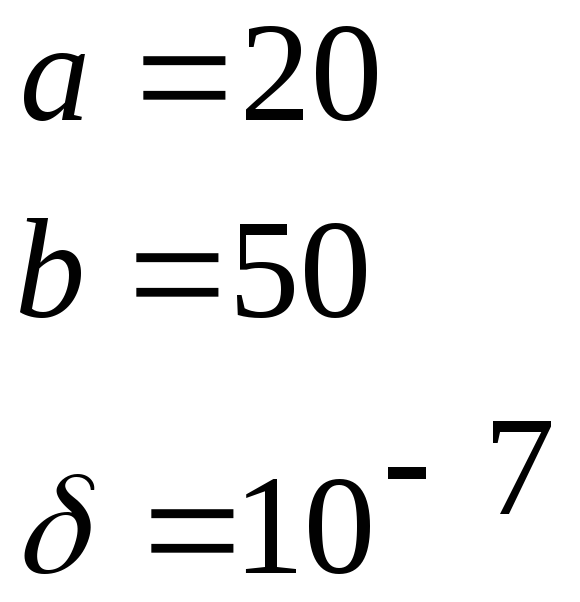, где

aиb- известные коэффициенты

Для расчета шага интегрирования найдем f_{э max}:

Для формул численного интегрирования прямоугольников , отсюда,

Для формул численного интегрирования трапеций , отсюда,

Выполним оценочный расчет разрядностей переменных

Воспользуемся формулой: ;

.

Отсюда, разрядность переменных .

Тогда, инструментальная погрешность , что должно удовлетворить требованиям решения задачи.

Программа

Ниже приведен листинг программы имитирующей работу ЦИС для математической зависимости . Программа обеспечивает вывод на экран пяти графиков функций: график эталонного вычисления математической зависимости на ПЭВМ арифметико-логическими методами, график вычисления математической зависимости на модели ЦИС с использованием метода численного интегрирования - прямоугольников, график вычисления математической зависимости на модели ЦИС с использованием метода численного интегрирования - трапеций и два графика ошибок для каждого из методов.

#include <graphics.h>

#include <math.h>

#include <stdlib.h>

#include <stdio.h>

#include <conio.h>

float f (float x);

int init ();

int x0 = 59; // x0, y0 - координаты

int y0 = 450; // начало координат в пикселах

float xn = 1; // начальное значение x

float xm = 20; // максимальное значение x

float hx = xm/(637-x0); // изменение x при шаге в один пиксел

float hy = f (xn)/(y0 - 2); // среднее изменение y при шаге в один пиксел

int main() {

if (init () == 1) exit (1);

// Блок переменных для образца

float sx1 = x0 + xn/hx; // вычисляем пиксел, соответствующий xn

float sy1 = y0 - f (xn)/hy;

float sx2 = sx1 + 1; // вычисляем пиксел, соответствующий xn + hx

float sy2 = y0 - f (xn + hx)/hy;

// Блок переменных для прямоугольников

float ry = f (xn);

float ry1 = y0 - ry/hy;

float ry11 = 60*xn;

float ry4 = -ry*ry;

float ry9 = ry4/2;

float ry8 = 1/(2*sqrt (30*xn - 25));

float ry5 = -2*ry;

float rdy11 = 60*hx;

float rdy7 = rdy11*hx;

float rdy3 = ry8*rdy7;

float rdy = ry4*rdy3;

float rdy4 = ry5*rdy;

// Блок переменных для трапеций

float ty = f (xn);

float ty1 = y0 - ty/hy;

float ty11 = 60*xn;

float ty4 = -ty*ty;

float ty9 = ty4/2;

float ty8 = 1/(2*sqrt (30*xn - 25));

float ty5 = -2*ty;

float tdy11 = 60*hx;

float tdy7 = tdy11*hx;

float tdy3 = ty8*tdy7;

float tdy = ty4*tdy3;

float tdy4 = ty5*tdy;

// Блок переменных для ошибки по прямоугольникам

float erry1 = y0 - fabs (ry1 - sy1);

// Блок переменных для ошибки по трапециям

float erty1 = y0 - fabs (ty1 - sy1);

for (int i = 2; sx2 <= 638; i++) {

// Блок построения образца

setcolor (LIGHTBLUE);

line (sx1, sy1, sx2, sy2); //чертим первый отрезок, соответствующий//точкам (xn; f (xn)), (xn + hx; f (xn + hx))

// Блок построения по прямоугольникам

setcolor (MAGENTA);

ry11 += rdy11;

rdy7 = ry11*hx;

float rdy9 = rdy4/2;

ry9 += rdy9;

float rdy8 = ry9*rdy3;

ry8 += rdy8;

float rdy5 = -2*rdy;

ry5 += rdy5;

rdy4 = ry5*rdy;

ry4 += rdy4;

rdy3 = ry8*rdy7;

float rdy = ry4*rdy3;

ry += rdy;

int ry2 = y0 - ry/hy; // Собственно построение

line (sx1, ry1, sx2, ry2);

// Блок построения ошибки прямоугольников

setcolor (LIGHTCYAN);

float erry2 = y0 - fabs (ry2 - sy2);

line (sx1, erry1, sx2, erry2);

ry1 = ry2;

erry1 = erry2;

// Блок построения по трапециям

setcolor (GREEN);

ty11 += tdy11;

tdy7 = (ty11 + tdy11/2)*hx;

float tdy9 = tdy4/2;

ty9 += tdy9;

float tdy8 = (ty9 + tdy9/2)*tdy3;

ty8 += tdy8;

float tdy5 = -2*tdy;

ty5 += tdy5;

tdy4 = (ty5 + tdy5/2)*tdy;

ty4 += tdy4;

tdy3 = (ty8 + tdy8/2)*tdy7;

tdy = (ty4 + tdy4/2)*tdy3;

ty += tdy;

int ty2 = y0 - ty/hy;// Собственно построение

line (sx1, ty1, sx2, ty2);

// Блок построения ошибки по трапециям

setcolor (YELLOW);

float erty2 = y0 - fabs (ty2 - sy2);

line (sx1, erty1, sx2, erty2);

ty1 = ty2;

erty1 = erty2;

sx1 += 1; // сдвигаем "экранные иксы"

sx2 += 1;

sy1 = sy2; // сдвигаем "экранный y" образца

sy2 = y0 - f (xn + i*hx)/hy; // вычисляем следующий y образца, соответствующий значению f от (текущего x плюс hx)

}

getch ();

return (0);

}

float f (float x) {

return 1/sqrt(30*x*x-25);

}

int init () {

/* request auto detection */

int gdriver = DETECT, gmode, errorcode;

/* initialize graphics mode */

initgraph (&gdriver, &gmode, "f:\\bc\\bgi");

/* read result of initialization */

errorcode = graphresult ();

if (errorcode != grOk) { /* an error occurred */

printf ("Graphics error: %s\n", grapherrormsg(errorcode));

printf ("Press any key to halt:");

getch ();

return (1); /* return with error code */

}

setcolor (LIGHTGRAY);

// чертим оси координат

line (x0, y0, x0, 0);

line (x0, y0, x0, 450);

line (x0, y0, 59, y0);

line (x0, y0, 639, y0);

setcolor (WHITE);

// рисуем стрелочки

line (630, y0 - 2, 639, y0); // на оси Ox

line (630, y0 + 2, 639, y0);

line (x0 - 2, 9, x0, 0); // на оси Oy

line (x0 + 2, 9, x0, 0);

// проставляем координатные отрезки на оси Ox

outtextxy (x0 - 10, y0 + 5, "0");

outtextxy (632, y0 + 5, "x");

char *buf;

for (int i = 1; i <= 9; i++) {

line (x0 + (639 - x0)*i/10, y0, x0 + (639 - x0)*i/10, y0 + 4);

outtextxy (x0 + (639 - x0)*i/10, y0 + 5, gcvt (xm*i/10, 2, buf));

}

// проставляем координатные отрезки на оси Oy

outtextxy (x0 - 10, 0, "y");

for (i = 1; i <= 9; i++) {

line (x0, y0 - y0*i/10, x0 - 4, y0 - y0*i/10);

outtextxy (x0 - 59, y0 - y0*i/10, gcvt (f (xm)*i/10, 2, buf));

}

setcolor (LIGHTRED);

// чертим асимптоту

line (x0 + sqrt (5.0/6)/hx, 0, x0 + sqrt (5.0/6)/hx, 450);

// рисуем пояснения

setcolor (MAGENTA);

line (514, 3, 543, 3);

outtextxy (545, 0, " - rect");

setcolor (GREEN);

line (514, 13, 543, 13);

outtextxy (545, 10, " - trap");

setcolor (LIGHTBLUE);

line (514, 23, 543, 23);

outtextxy (545, 20, " - smpl");

setcolor (LIGHTCYAN);

line (514, 33, 543, 33);

outtextxy (545, 30, " - err rect");

setcolor (YELLOW);

line (514, 43, 543, 43);

outtextxy (545, 40, " - err trap");

return (0);

}

5

2

Рис. 3.1. Структурная схема параллельной цифровой интегрирующей системы,

воспроизводящей решение СУШ функции

.7.2 Программа моделирования функции, с использованием методов ЦИС

Расчет параметров ЦИС:

1. Соотношение порядков формул

а) m = 0 (для формулы прямоугольников)

б) m = 1 (для формулы трапеций)

2. Экстраполяция приращений

а) (для формулы прямоугольников)

б) (для формулы трапеций)

3. Расчет . Данный параметр являетсяmax скоростью изменения функций. На интервале все функции, входящие в состав СУШ являются гладкими, следовательно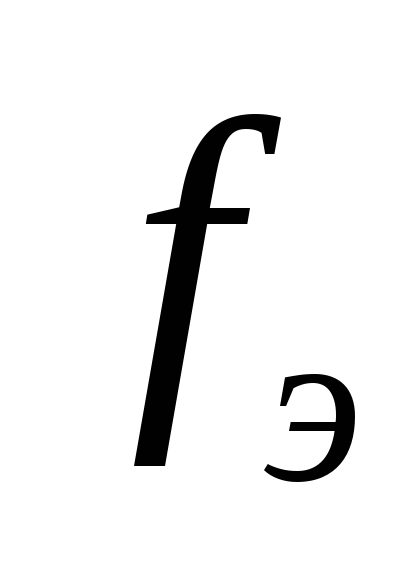является частотой периодических функций, входящих в СУШ, и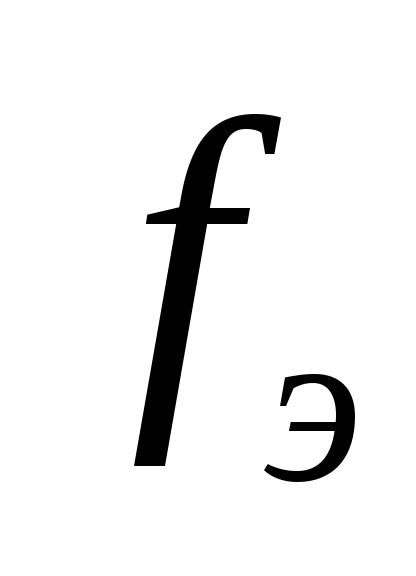= 35 Гц.

4. Шаг интегрирования

а) (для формулы прямоугольников)

б) (для формулы трапеций)

5. Расчет разрядной сетки интегратора

а) Разрядная сетка для представления значения функции ,n = 22

б) Разрядная сетка для представления приращений ,n = 6

в) Разрядная сетка для представления остатка

6. Расчет методической погрешности

а) М = (для формулы прямоугольников)

б) М = (для формулы трапеций)

Код программы:

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, TeEngine, Series, StdCtrls, ExtCtrls, TeeProcs, Chart, TeeFunci;

type

TForm1 = class(TForm)

Polotno: TChart;

DrowGraph: TButton;

initial: TLineSeries;

integral: TLineSeries;

stepOfIteration: TEdit;

Label1: TLabel;

Label2: TLabel;

Memo1: TMemo;

RadioGroup1: TRadioGroup;

RadioButton1: TRadioButton;

RadioButton2: TRadioButton;

RadioButton3: TRadioButton;

Button1: TButton;

model: TLineSeries;

remainder: TCheckBox;

errorGraph: TLineSeries;

procedure DrowGraphClick(Sender: TObject);

procedure Button1Click(Sender: TObject);

procedure FormCreate(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

integ,stepOfIterationReal,temp1:real;

arrayPointX : array[1..100] of real;

arrayPointY : array[1..100] of real;

buf:array [1..6] of byte;

error:integer;

workModeRemainder:Boolean;

newValue,oldValue : array[1..15] of double;

integratorsResults, functionValue : array [1..15] of double;

implementation

uses Math;

{$R *.dfm}

const

f=35;

length=1 ;

beginPoint = 0;

magnification = 1000;

// n=2;

maskN=000001;

maxYValues = 32;

w=70*pi;

function y3(x :real):real ;

begin

y3:=cos(w*x);

//functionValue[3]:=functionValue[3] + x;

//y3:=functionValue[3];

end;

function y5():real ;

begin

y5:=1/3;

end;

function y2(x :real):real;

var

temp:real;

begin

temp:= cos(w*x);

if temp>=0 then

y2:=exp((1/3)*ln(abs(temp)))

else

y2:=-exp((1/3)*ln(abs(temp)));

end;

function y11(x :real):real ;

begin

y11:=sin(w*x);

//functionValue[11]:=functionValue[11] + x;

//y11:=functionValue[11];

end;

function y8(x :real):real ;

var

temp:real;

begin

temp:= y2(x) ;

if not(temp=0) then

y8:=2/temp

else y8:=0;

//functionValue[8]:=functionValue[8] + x;

//y8:=functionValue[8];

end;

function y9():real ;

begin

y9:=2;

end;

function y4(x :real):real ;

var

temp:real;

begin

temp:= (3*sqr(y2(x))) ;

if not(temp=0) then

y4:=1/temp

else

y4:= 0;

//functionValue[4]:=functionValue[4] + x;

//y4:=functionValue[4];

end;

function Intgrator(x:real; i:integer) :real;

begin

integratorsResults[i]:= integratorsResults[i] + + x*stepOfIterationReal;

Intgrator:= integratorsResults[i];

end;

procedure bullet7(x:real);

begin

newValue[10]:=w*Intgrator(oldValue[1],7);

end;

procedure bullet6(x:real);

begin

//newValue[11]:=y3(oldValue[3])*Intgrator(oldValue[10],6);

newValue[11]:=y3(x)*Intgrator(oldValue[10],6);

end;

procedure bullet5(x:real);

begin

//newValue[3]:=y11(oldValue[11])*Intgrator(oldValue[10],5);

newValue[3]:=y11(x)*Intgrator(oldValue[10],5);

end;

procedure bullet3(x:real);

begin

//newValue[6]:=y8(oldValue[8])*Intgrator(oldValue[2],3);

newValue[6]:=y8(x)*Intgrator(oldValue[2],3);

end;

procedure bullet4(x:real);

begin

newValue[8]:=y9()*Intgrator(oldValue[2],4);

end;

procedure bullet2(x:real);

begin

newValue[4]:=y5()*Intgrator(oldValue[6],2);

end;

procedure bullet1(x:real);

begin

//newValue[2]:=y4(oldValue[4])*Intgrator(oldValue[3],1);

newValue[2]:=y4(x)*Intgrator(oldValue[3],1);

end;

procedure TForm1.DrowGraphClick(Sender: TObject);

var

x,e:real;

i,j:integer;

begin

for i:=2 to 15 do begin

newValue[i]:=0;

oldValue[i]:=0;

integratorsResults[i]:=0;

end;

x:=beginPoint;

while x<length do begin

bullet1(x);

bullet2(x);

bullet3(x);

bullet4(x);

bullet5(x);

bullet6(x);

bullet7(x);

for i:=1 to 15 do begin

oldValue[i]:=newValue[i];

end;

e:=e+oldValue[2];

initial.AddXY(x,e);

x:=x+ stepOfIterationReal;

end;

end;

end;

procedure TForm1.Button1Click(Sender: TObject);

begin

{if (stepOfIterationReal <> 0) then

// повторное интегрирование

memo1.Lines.Add('S='+FloatToStr(integratorRectangle(integral))); }

end;

procedure TForm1.FormCreate(Sender: TObject);

begin

stepOfIterationReal:=0;

end;

end.

Результаты моделирования

Результаты моделирования представлены графиком вывода значений Dy3, показанного на рисунке 5.5.

Рисунок 5.5 - Вывод графика Dy3

Библиографический список

1. ТОП 500. Список 500 самых мощных компьютеров мира.http://www.top500.org/. (20.12.2008г.).

2. SPEC CPU2000 Development. http://www.spec.org/ osg/cpu2000/.

3. Каган Б.М. Электронные вычислительные машины и системы: Учеб. пособие для вузов. – М.: Энергоатомиздат, 1985. - 552 с., ил.

4. Воеводин В.В. Вычислительная математика и структура алгоритмов. – М.: МГУ, 2006.-113 с. Ил.

5. Flynn M. Some Computer Organizations and Their Effectiveness. – IEEE Trans. on Computers, Sept., 1972.

6. Jouppi N. Superscalar versus Superpipelined Machines. – Computer Archetecture News, June, 1988.

7. Столлингс В. Структурная организация и архитектура компьютерных систем, 5-е изд. – М.: Издательсий дом «Вильямс», 2002. – 896 с. – ISBN 5-8459-0262-2.

8. El-Rewini H., Abd-El-Barr M. Advanced Computer Architecture and Parallel Processing. John Willey & Sons, New Jersey, 2005. – 272 p. – ISBN 0-471-46740-5.

9. Таненбаум Э. Архитектура компьютера. 4-е изд. – СПб.: Питер, 2003. – 704 с. – ISBN 5-318-00298-6.

10. Geist A., Beguelin A., Dongarra J., Jiang W., Manchek R., Sunderam V. PVM: Parallel Virtual Machine, A Users' Guide and Tutorial for Networked Parallel Computing. MIT Press, Massachusetts, 1994. – 176 p. – ISBN 0-262-57108-0.

11. Официальный веб-ресурс: http://www.csm.ornl.gov/pvm/

12. Snir M., Otto S., Huss-Lederman S., Walker D., Dongarra J. MPI: The Complete Reference Volume 1. MIT Press, Massachusetts, 1998. – 448 p. – ISBN 0-262-69215-5.

13. Snir M., Otto S., Huss-Lederman S., Walker D., Dongarra J. MPI: The Complete Reference Volume 2 – The MPI-2 Extensions. MIT Press, Massachusetts, 1998. – 363 p. – ISBN 0-262-57123-4.

14. Официальный веб-ресурс: http://www.mpi-forum.org/

15. Каляев А. В. Теория интегрирующих машин и структур. - М.: Сов. радио, 1970. -.659 с., ил.

ОГЛАВЛЕНИЕ

Введение…………………………………………….………..	3
1. Основные понятия высокопроизводительных вычислений……………………………………..................	4
1.1 Характеристики и требования высокоскоростной обработки…………………….….	4
1.2 Способы повышения скорости обработки………..…	8
2 Взаимосвязь структур алгоритмов и исполнителей…..…	14
3 Структурная организация высокопроизводительных вычислительных систем………………………………….	17
3.1 Классификация ВС по Флину………………………..	18
3.2 Параллелизм на уровне команд……………………...	21
3.3 Параллелизм на уровне процессоров………………..	35
4 Параллельные алгоритмы в задачах сортировки………...	53
4.1 Проблемы сортировки на вычислительных машинах параллельного действия…………………..	54
5 Методы построения распределенных алгоритмов на основе понижения порядка производной……………….	64
5.1 Переход от произвольной математической зависимости к системам дифференциальных уравнений……………………………………………..	64
5.2 Методы численного интегрирования по Стилтьесу……………………………………………...	68
5.3 Разностно-квантованные схемы интегрирования уравнений Шеннона в относительной форме записи………………………………………………….	72
5.4 Примеры реализации формальных методов перехода от произвольной математической зависимости к системам дифференциальных уравнений………………………………………………	75
5.5 Разностно-квантованные схемы интегрирования. Расчет основных параметров ЦИС………………….	81
5.6 Задания для самостоятельного выполнения………...	85
5.7 Примеры выполнения заданий……………………….	91
Библиографический список………………………………	111

73