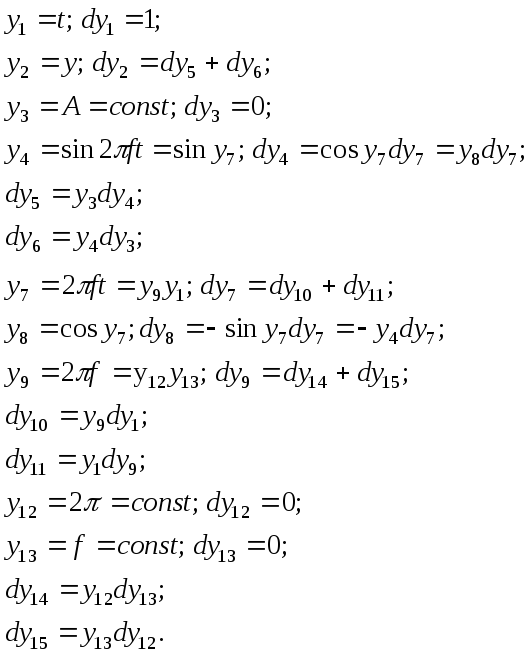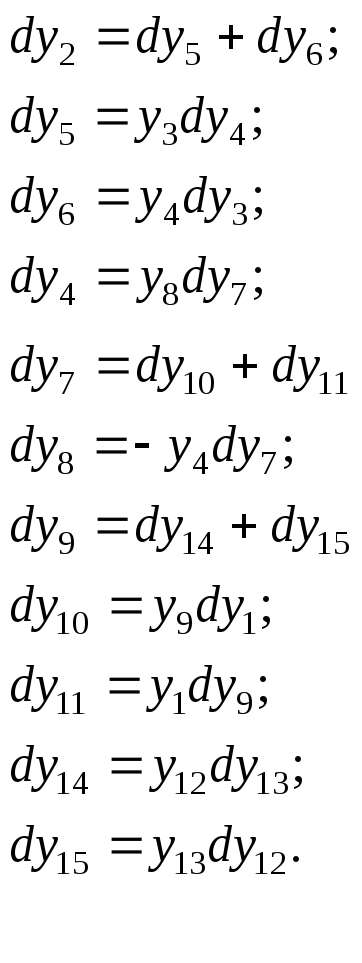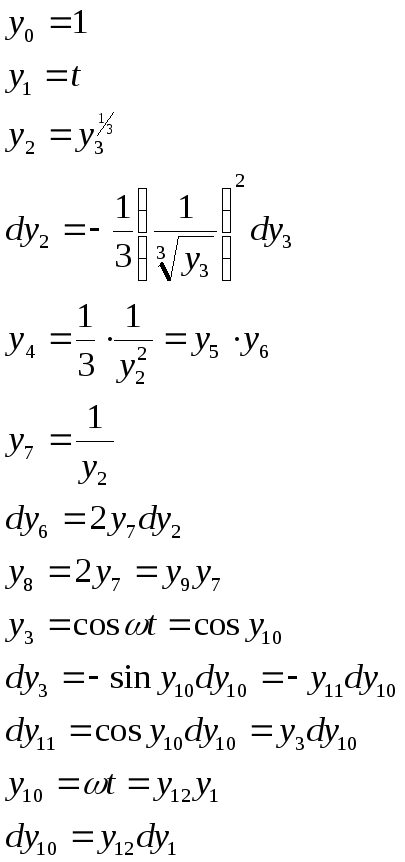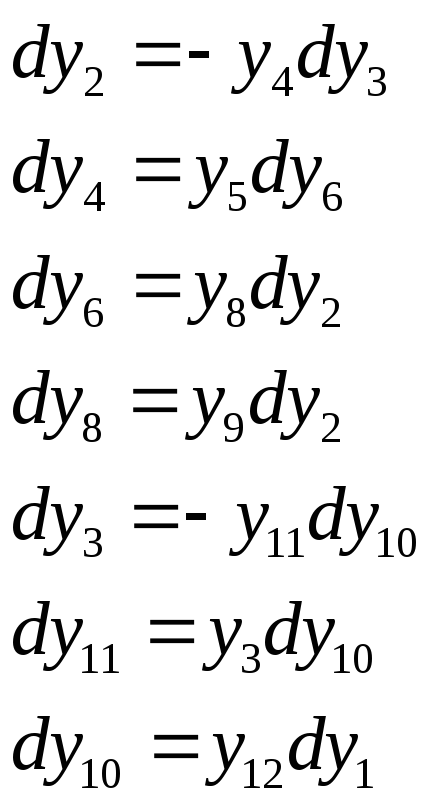5.4 Примеры реализации формальных методов перехода от произвольной математической зависимости к системам дифференциальных уравнений

- Пусть задана функция , гдеи задана погрешность вычисления.

Тогда, используя вышеизложенную методику приведем исходную математическую зависимость к системе дифференциальных уравнений К.Шеннона (СУШ). В таблице 5.4 приведены обозначения, подстановки и последовательность получения дифференциальных уравнений СУШ.

Структурная схема связей решающих блоков, отображающая параллельный вычислительный процесс исходной математической зависимости в цифровой интегрирующей системе показана на рисунке 5.2

Таблица 5.4 Последовательность перехода к СУШ

Обозначения, подстановки	СУШ

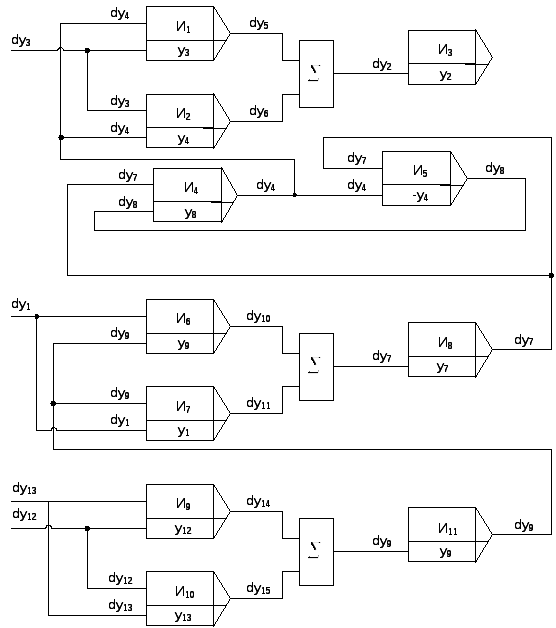
Рисунок 5.2 - Структурная схема связей решающих блоков СУШ для математической зависимости

С целью сокращения числа переменных неизвестных на шаге i + 1 выполним ранжирование системы дифференциальных уравнений:

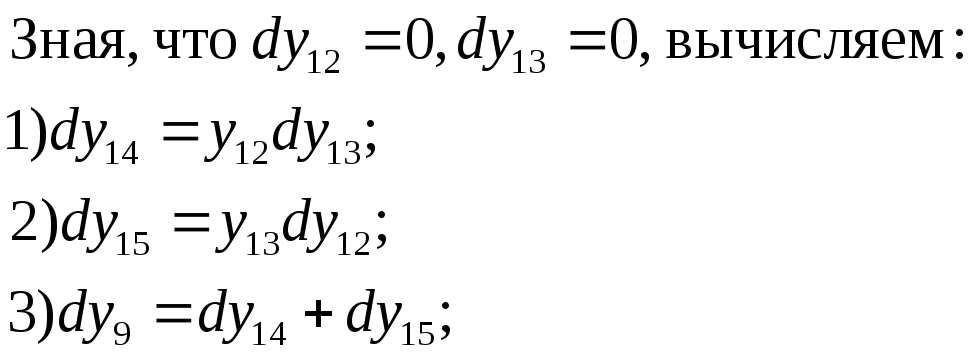
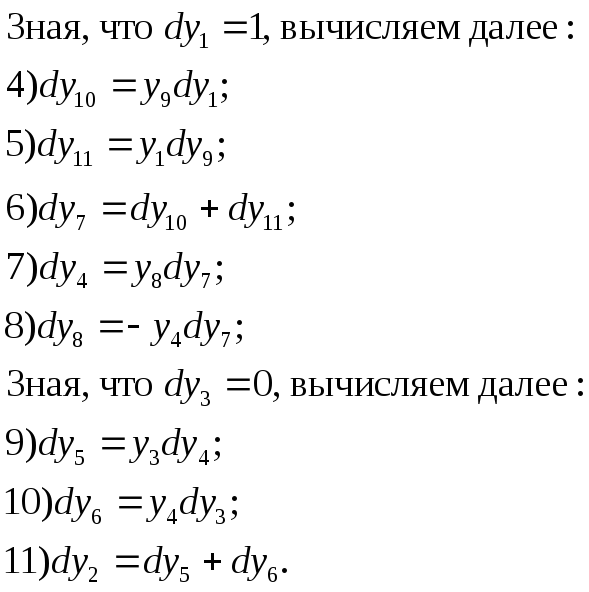
Выбирая один из возможных способов численного решения, перейдем к интерполяционным формулам численного интегрирования по Стилтьесу:

Для формулы численного интегрирования прямоугольников (m=0) система имеет следующий вид:

Для формулы численного интегрирования трапеций (m=1) система имеет следующий вид:

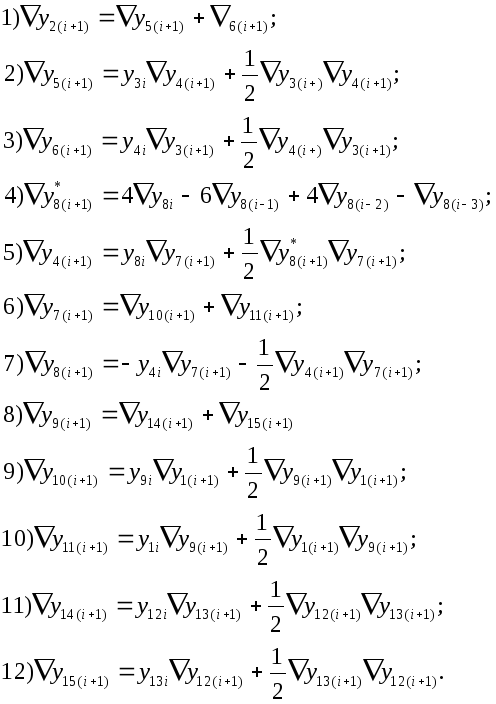
- Пусть задана функция , тогда система дифференциальных уравнений Шеннона по рассмотренной выше методике будет иметь следующий вид (таблица 5.5):

Функция	Подстановки	СУШ

Таблица 5.5 СУШ функции

Структурная схема параллельной интегрирующей системы воспроизведения заданной математической зависимости имеет вид (рисунок 5.3):

Рисунок 5.3 Структурная схема связей решающих блоков СУШ для математической зависимости

5.5 Разностно-квантованные схемы интегрирования. Расчет основных параметров цис

Расчет заключается в выборе оптимальных соотношений порядков формул численного интегрирования, экстраполяции приращений, самих формул, разрядности значений переменных, приращений, шага интегрирования, способа округления, обеспечивающих требуемую погрешностьна всем интервале интегрирования заданных математических зависимостей и шаге выдачи решений.

Общая погрешность решения задач в ЦИС на большом интервале интегрирования зависит от ошибки метода, квантования первого и второго рода, инструментальной погрешности, трансформируемой(определяемой, как способом представления исходных математических зависимостей так и в последствии коммутацией цифровых интеграторов в соответствии с решаемой задачей)

(5.16)

В этой связи аналитически выбрать не завышенные параметры ЦИС не представляется возможным.

Оценка общих погрешностей, возникающих при решении в ЦИС различных конкретных задач, в большинстве случаев производится путем интегрирования системы дифференциальных уравнений погрешностей [15] или моделированием на ЦВМ широкого применения. Однако в обоих случаях прежде необходим ориентировочный начальный выбор параметров ЦИС, которые в дальнейшем были бы уточнены.

Порядок формулы численного интегрирования определим из условия, согласно которому предельная методическая погрешностьпри вычислении интегралов СУШ

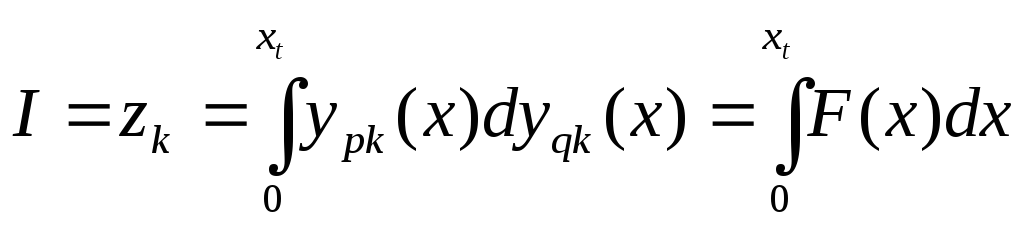(5.17)

не должна превышать половины предельной абсолютной ошибки вычислений , то есть . Здесь - некоторая эквивалентная функция. В общем случае . Но, учитывая, что методическая ошибка формул численного интегрирования в основном определяется скоростью изменения подынтегральной функциина каждом шаге интегрирования, в качестве удобно использовать хорошо интегрируемую периодическую функцию, например, , имеющую предельно допустимую скорость изменения такую же, как и функция СУШ. Используя общую формулу методической погрешности на одном шаге интегрирования при вычислении интеграла Римана[15] получим

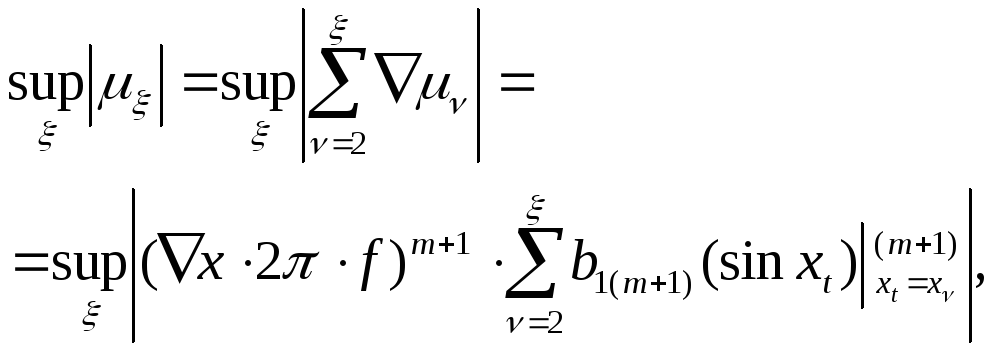(5.18)

где - известные коэффициенты. Заменяя алгебраическую сумму приращенийинтегралом, находим

(5.19)

Если , томожно представить в виде

, (5.20)

тогда получаем

. (5.21

В этом неравенстве величины - шаг интегрирования и- относительная приведенная погрешность известны (или задаются исходя из требований решения задачи)- максимальная циклическая частота эквивалентной функции синус, определяемая скоростью изменения переменных СУШ, которую требуется найти. Предположим, что каждая переменная СУШ меняется по закону синуса

, тогда .

Приравнивая в последнем выражении определим максимальное значение частотыдля каждой функции. Поскольку в принятых условиях этому будет соответствовать, то

. (5.22)

Значения рассчитываются для каждой функции системы уравнений Шеннона. Так как оценочный расчетвыполняется по предельно допустимым максимальным значениям, то в качествевыбирается значение

. (5.23)

Порядок формулы экстраполяции системы выбирается из условия, при котором замена переменных или приращений их экстраполированными значениями не привела бы к существенному увеличению приращения методической ошибки. Оно выполняется, если

. (5.24)

Неравенство (5.24) соблюдается, когда порядок малости величины , входящей в качестве коэффициента в выражение для, выше или равен порядку малости коэффициентаформулы методической погрешности[15]:

, (5.25)

откуда . Формулы экстраполяции, представленные в таблице 5.3, приведены с учетом неравенства (5.25).

Оценка погрешностей квантования для различных формул численного интегрирования показывает, что условие

(5.26)

при принятых алгоритмах численного интегрирования и экстраполяции выполняется, если

. (5.27)

Число разрядов приращений,,зависит от шага интегрирования, предельных скоростей и значений изменения переменных СУШ, согласно которым

. (5.27)

Зная предельную величину относительного приращения , значениеможно определить по формуле

. (5.28)

Найденные значения параметров ЦИС позволяют также приближенно оценить время выполнения основных операций интегрирования и экстраполяции: .