Для машиностроения Мех.мат / Лекция №13-механика

Лекция №13

Тема: «Геометрические характеристики сечения»

Вопросы:

1. Статические моменты сечения

2. Моменты инерции сечения

3. Моменты инерции прямоугольника, круга и кольца

4. Изменение моментов инерции с поворотом осей. Главные оси и главные моменты инерции

1. Статические моменты сечения

Статическим моментом сечения относительно оси X (см. рис. 1) называется выражение:

(1)

и относительно оси Y:

(2)

Рис. 1

Статический момент имеет размерность см³ или м³, может быть положительным, отрицательным или равным нулю. Если статический момент ранен нулю, то ось проходит через центр тяжести сечения и называется центральной осью. Поэтому оси симметрии фигур вceгда являются центральными.

Определим как изменяется статический момент фигуры с параллельным переносом оси. Пусть ось Х_о является центральной (см. рис. 2), а ось X смещена на расстояние а. Из рисунка видно, что: .

Рис. 2

Статический момент фигуры относительно оси X равен:

.

Интеграл представляет собой статический момент относительно оси Х_о, т.е. центральной оси. Мы уже отмечали, что статические моменты относительно центральных осей равны нулю.

;

В результате получим:

или

.

Если заменить – ординату центра тяжести фигуры, то получим:

и (2)

По формулам (2) можно определить координаты центра тяжести фигуры. Если фигура имеет сложные очертания, то ее разбивают на несколько простых (прямоугольники, треугольники, секторы, сегменты и т.д.) и статический момент находят как сумму статических моментов простых фигур. Статический момент простых фигур определяют, преобразовав формулу (2):

и (3)

Пример: Определить центр тяжести фигуры (рис. 3). Размеры даны в см.

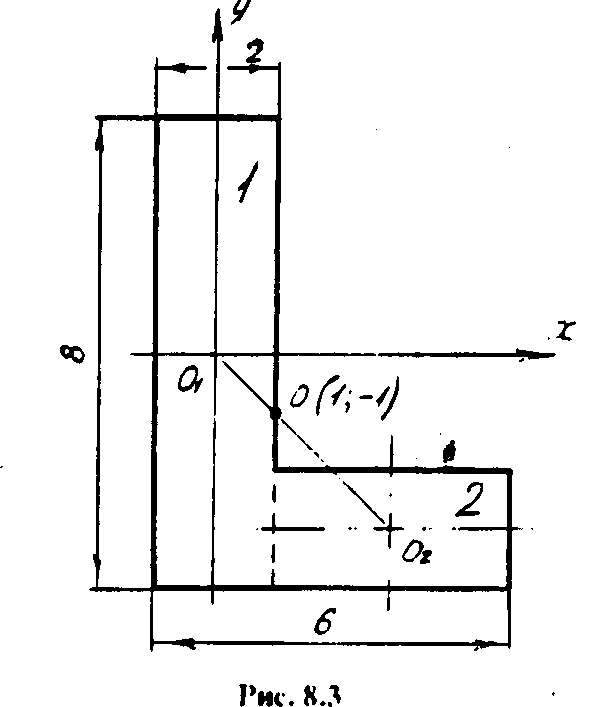
Рис.3

Решение: Разбиваем фигуру на два прямоугольника (на рисунке пронумерованы 1 и 2). Оси X и Y проводим чeрез центр тяжести одной из фигур (прямоугольника 1), что значительно облегчает подсчеты, так как:

.

По формуле (3) находим:

,

.

Общая площадь фигуры равна:

.

Координаты центра тяжести определим по формуле (2):

;

.

Проверка: Если фигура вычерчена в масштабе, то центр тяжести находится па прямой, соединяющей центры тяжести простых фигур.

2. Моменты инерции сечения

Осевым моментом инерции относительно оси X называется выражение:

относительно оси Y: (4)

Полярным моментом инерции является выражение (см. рис. 4):

(5)

Осевые и полярный моменты инерции всегда положительны и имеют размерность см⁴ или м⁴. Из рисунка 4 видно, что:

поэтому:

Рис. 4

или

(6)

Полярный момент инерции равен сумме осевых.

Помимо осевых и полярного момента инерции в ряде случаев определяют центробежный момент:

. (7)

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Размерность та же, что и осевых и полярных моментов – см⁴ или м⁴.

Определим, как изменяется осевой момент инерции с параллельным переносом оси. Пусть ось Х_о – центральная (см. рис. 2). Из рисунка видно, что:

,

Тогда:

Интеграл – это момент инерции относительно центральной оси Х_о, т.е. интеграл – это статический момент относительно центральной оси, а он всегда равен нулю.

В результате получим:

(8)

Из формулы (8) видно, что осевой момент минимальный при а=0, т.е. центральный осевой момент имеет наименьшее значение.

Рассмотрим изменение центробежного момента инерции с параллельным переносом осей (см. рис. 5). Оси X_о и Y_о – центральные.

Рис.5

Из рисунка 5 видно, что:

, .

Центробежный момент равен:

Интеграл представляет собой центробежный момент инерции, интегралы и – статические моменты относительно центральных осей X_о и Y_о. Как известно, центральные статические моменты равны нулю. Поэтому:

(9)

Если одна из центральных осей являйся осью симметрии фигуры, то и формула (9) упростится:

(10)

3. Моменты инерции прямоугольника, круга и кольца

3.1. Осевой момент прямоугольника

Определим центральный осевой момент прямоугольника. Возьмем бесконечно тонкую полоску толщиной dy на расстоянии y от оси X (рис. 6). Тогда:

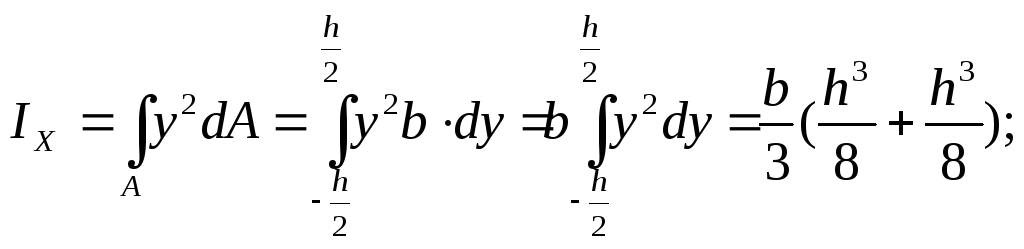
(11)

Рис. 6

3.2. Моменты инерции круга и кольца

Определим полярный момент инерции круга. Возьмем бесконечно тонкое кольцо толщиной на расстоянии от центра круга (рис.7). Площадь кольца можно определить, развернув прямоугольник.

.

Полярный момент равен:

Обычно при подсчетах пользуются не радиусом, а диаметром:

и ,

(12)

Полярный момент инерции фигуры равен сумме осевых моментов:

,

но для круга , поэтому:

(13)

Моменты инерции кольца можно определить как разность моментов инерции большого и малого кругов (рис. 8).

Рис.7 Рис.8

или

(14)

где ;

(15)

4. Изменение моментов инерции с поворотом осей. Главные оси и главные моменты инерции

Определим, как изменяются осевые моменты инерции с поворотом осей. Пусть оси X и Y проходят под углом к осям X₁ и Y₁ (см. рис. 9)

С поворотом осей значение осевых и центробежных моментов инерции меняются. Для практических целей весьма важно определить положение осей, когда осевой момент максимальный и минимальный. При максимальном моменте сопротивление изгибу наибольшее, при минимальном – наименьшее. Оси, относительно которых осевые моменты имеют экстремальные значения, называют главными осями.

Положение осей, когда центробежный момент инерции равен нулю, также соответствует главным осям, т.е. если , то X и Y – главные оси.

Рис. 9

Формула для определения положения двух осей, относительно одной из которых осевой момент инерции максимален, а относительно другой – минимален имеет следующий вид:

(16)

Моменты инерции относительно главных осей называются главными моментами инерции. Главные моменты инерции имеют максимум и минимум. Они определяются по формуле:

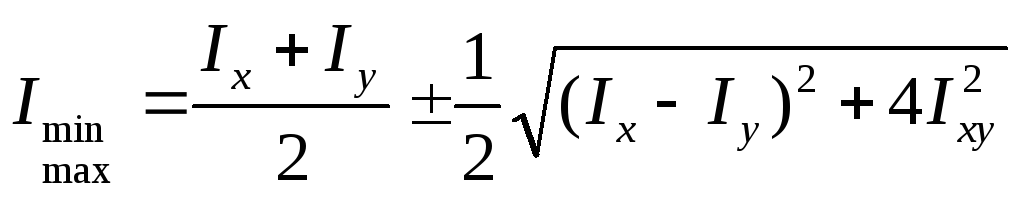(17)

Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.

Во многих случаях удается сразу определить положение главных центральных осей. Если фигура имеет ось симметрии, то она является одной из главных центральных осей, вторая проходит через центр тяжести сечения перпендикулярно первой. Сказанное следует из того, что относительно оси симметрии и любой оси, ей перпендикулярной, центробежный момент инерции равен нулю.

В случае если два главных центральных момента инерции сечения равны между собой, то у этого сечения любая центральная ось является главной, и все главные центральные моменты инерции одинаковы (круг, квадрат, шестиугольник, равносторонний треугольник).