3) (27: 3) – 3 – Было тетрадей у Алеся

5-ый способ – решение задачи по действиям с частичными пояснениями результатов:

1. 3 + 3 + 3 = 9 (т.).

2. 27 + 9 = 36 (т.).

3. 36 : 3 = 12 (т.) – было тетрадей у Лени.

4. 12 – 3 = 9 (т.) – было тетрадей у Миши.

5. 9 – 3 = 6 (т.) - было тетрадей у Алеся.

Алгебраический способ решения

Используя чертёж задачи, составим уравнение.

Х – количество тетрадей у Алеся,

Х + 3 – количество тетрадей у Миши,

(Х + 3) + 3 – количество тетрадей у Лёни.

Уравнение: Х + (Х + 3) + (Х + 3) + 3 = 27. Используя переместительное и сочетательное свойства сложения, имеем: (Х + Х + Х) + (3 + 3 + 3 ) = 27.

Заменив сложение умножением, запишем уравнение:

Х·3 + 3 · 3 = 27 Решаем уравнение: Х·3 + 9 = 27.

Х·3 = 27 – 9

Х·3 = 18

Х = 18: 3

Х = 6

6 + (6 + 3) + (6 + 3) + 3 = 27

27 = 27

Ответ: было тетрадей : у Алеся–6, у Миши – 9, у Лёни – 12.

Проверка решения: 6 + 9 + 12 = 27 (т.).

Геометрический способ решения

А. Используя чертёж, найдём

М. 3 т 27 т. сумму отрезков

Л. 3 т.

У Алеся У Миши У Лёни

Перенесём три длинных и три коротких отрезка в один отрезок: 3 3 3

27 т.

Как известно, один маленький отрезок моделирует 3 тетради, а 3 таких же отрезка 3·3=9 (т.), три больших отрезка моделируют 27–9=18 (т.). Один большой отрезок моделирует 18:3=6 (т.) – количество тетрадей у Алеся. У Миши тетрадей 6+3=9 (т.), а у Лёни 9+3=12 (т.).

Дополнительная работа над задачей

1. Выбор рационального способа решения после её решения несколькими способами.

2. Объяснение выражений, составленных по условию задачи: обычно возникают трудности в пояснении выражений: 3 + 3 + 3, 27 – 9, 27 + 9.

3.Выбор модели к задаче зависит от вида и способа реше-ния задачи. Модель должна полностью представлять все

числовые данные, отношения и зависимости задачи, под- чёркивая наиболее существенные из них, их структуру.

4. Изменение текста задачи, чтобы исследовать, к какому решению это приведёт. Вначале мы значитель-но изменили текст задачи, сделали его удобным к понима-нию как по форме, так и по содержанию.

Способы проверки решения задачи:

1) прикидка результата; 2) решение задачи другим способом; 3)решение задачи, обратной данной; 4)установление соответствия всем числовым данным и отношениям задачи.

Способы исследования решения задачи

1.Влияние изменения вопроса задач на её ответ

2. Влияние изменения условия на ответ задачи.

3. Влияние изменения числовых данных на ответ задачи.

4. Влияние изменения отношений на ответ задачи.

5.Влияние изменения величин задачи на ответ

6.Влияние изменения формулировки на ответ

Младшие школьники испытывают большие трудности в поиске способа решения сюжетных, особенно нестандартных задач, прежде всего из-за неразработанности методики их решения.

следующие этапы работы над задачей:

1. Ознакомление с текстом задачи. Выделение условия, вопроса, известных и неизвестных данных, искомого.

2. Моделирование задачи (краткая запись, чертёж, таблица, схема, граф-схема и др.).

3. Поиск способа решения задачи с помощью аналитико-синтетического способа разбора.

4. Осуществление решения.

5. Проверка и оценка полученного результата.

Главным этапом работы над задачей является третий, связанный с аналитико-синтетической поисковой деятельностью учащихся, с выдвижением предположений о способах решения задачи с их последующей проверкой. Обычно этот поиск сводится к распознаванию знакомых элементов в тексте задачи и её решению по аналогии с ранее решёнными учеником задачами.

Значительно повысить эффективность поиска способов решения может семантический анализ текста задачи. Для этого пользуются ключевыми словами и словосочетаниями типа больше (меньше) на, больше (меньше) в, вместе, взяли по, было – осталось и др. Обычно эти слова и словосочетания требуют выполнения определён-ных арифметических действий, для чего учащимся необходимо сделать выбор. Но он, к сожалению, связан со значительными трудностями для них. Например, отношения больше на, больше в в большинстве задач требуют выполнения действий сложения и умножения соответственно. Однако в задачах в косвенной форме и задачах на сравнение необходимо выполнять противоположные или обратные арифметические действия, что приводит к многочисленным ошибкам даже у учащихся старших классов. Избежать этих трудностей возможно при помощи семантического анализа текста задачи.

При семантическом анализе текст задачи обычно разбивается на отдельные части – слова или словосочетания, каждое из которых является словесной моделью определённого элемента задачи. В результате по названию или наименованию выделяются величины, их значения и особенности значений, отличающие от других значений той же величины, известные, неизвестные и искомые значения величины. Кроме того, в тексте сюжетной задачи могут иметься словесные описания соотношений, которыми связаны заданные в задаче значения величин. Так, например, слова – признаки на … меньше (больше) указывают на отношение разностного сравнения. Эти словосочетания можно заменить сочетанием предлога на с одним из слов из пары слов-омонимов: длиннее – короче, глубже – мельче, быстрее – медленнее, дороже – дешевле, шире – уже, выше – ниже, тяжелее – легче, старше – моложе, дальше – ближе, позже – раньше и др. Отношение кратного сравнения задаётся таким же образом, лишь вместо предлога на используется предлог в. Кроме того, в признак этого отношения входит слово раз.

Если в условии задачи нет слов-признаков вида соотношения, тогда характер соотношения устанавливается лишь по наличию в условии значений взаимосвязанных величин. Решающий должен знать характер зависимости между этими величинами, например, между тройками величин: ценой – количеством – стоимостью, скоростью – временем – расстоянием, длиной – шириной – площадью прямоугольника и др. Обычно значение одной из этих величин есть произ–ведение значений остальных двух величин, например, значение расстояния равно произ–ведению значений скорости и времени. По этой зависимости можно найти одно из значений величины по двум известным значениям.

По мнению многих учёных, каждая сюжетная задача является словесной моделью некоторой реальной (задачной) ситуации. Обычно учащиеся чаще всего с помощью учителя пытаются воссоздать из текста задачи эту реальную ситуацию и, исходя из неё, решать задачу. Однако этого часто бывает недостаточно для получения ответа задачи. Поэтому целесообразно с помощью семантического анализа текста задачи установить все соотношения и зависимости между величинами, заданными в задаче, а затем по ним найти решение задачи.

Для проведения семантического анализа текста задачи можно воспользоваться следующим алгоритмическим предписанием:

1. Установить количество величин, представ-ленных в задаче, по их названию или же по наименованию при значениях этих величин.

2. Определить, сколько и какие значения этих величин заданы в задаче. Обычно каждое значение величины состоит из трёх частей: названия величины, особенности этого значения и наименования этого значения, если это значение известно. Если наименование не указано, то значение является неизвестным. И если в дополнение к этому в задание этого значения входит вопрос сколько? или требование найти, то это значение искомое.

3. Если величина задана тремя и более значениями, то ищут слова-признаки было или было – осталось (если их нет, то следует попытаться их вставить). Местоимение всего или его синоним указывает, что значение, к которому относится это слово, является суммой всех остальных значений. При наличии глаголов было - осталось значение, к которому относится слово было, является уменьшаемым, а значение, к которому отно-сится глагол осталось, является разностью.

4. Если величина задана двумя значениями, то высказывается предположение, что эти значения связаны соотношениями сравнения. При наличии местоимения столько же или его синонима имеет место соотношение равенства. Если имеется предлог на в сочетании со словом больше или меньше, то данные значения связаны соотношением разностного сравнения. Если же в тексте задачи стоит предлог в в сочетании с одним из этих слов и словом раз или же со словами составляет … часть, то это указывает на соотношение кратного сравнения. Если при значении стоит предлог в или слова часть (частей), то значение есть результат кратного отношения.

5. Если имеются в задаче три разные величины, каждая из которых задана одним своим значением, то при наличии предлога по в сочетании с местоимением всего и словом раз говорит о том, что значение, при котором стоит слово всего, есть произведение остальных двух значений, то есть делимое.

Приведём пример семантического анализа текста задачи: Миша купил 12 марок, что втрое больше, чем Коля. Сколько марок купили оба мальчика? Переформулируем задачу: Миша купил 12 марок. Это в 3 раза больше, чем Коля. Сколько всего марок купили оба мальчика?

В задаче представлена одна величина - количество. Эта величина имеет три значения (одно известное – 12 марок, два неизвестных (количество марок, купленных Колей, и количество купленных марок вместе). Последнее значение является искомым. Отношение в 3 раза больше относится к известному значению, выраженному числом 12, на что указывает частица это. По приведенному предписанию число 12 является произведением неизвестного числа и числа 3, равного кратному отношению. Откуда неизвестное число равно 12:3=4 (марки). Местоимение сколько в сочетании со словом всего указывает на то, что искомое число (ответ) равно сумме двух значений количества (известного и найденного): 12+4=16 (марок).

Таким образом, существуют два способа анализа поиска решения сюжетных задач: традиционный, связанный с анализом модели реальной задачной ситуации, и нетрадицион–ный – семантический анализ тек–ста задачи. Второй способ дополняет первый и должен применяться в качестве вспомогательного для правильного выбора одного из нескольких правдоподобных арифметических действий при поиске решений составных текстовых задач с помощью традиционных методов их разбора. НАВУЧАННЕ РАШЭННЮ ТЫПАВЫХ ЗАДАЧ на знаходжанне лікаў па іх суме і рознасці, па двух рознасцях, па суме (рознасці) і кратнай адносіне

Задача 1. Бідон з малаком важыць 44 кг, а без малака - на 36 кг лячэй.Колькі важаць бідон і малако паасобку?

Задачу зручна рашаць мадэляваннем яе адрэз-камі і шляхам ураўнівання па розных велічынях.

Б. - !---! ? кг 44кг

М.- !---!------------36 кг ------------! -? кг

Спосаб 1 - ураўніванне па масе малака

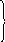
Б. - !---!..........................................! кг 44+36(кг)

М.- !---!------------36 кг ------------! -? кг

1) 44+36 = 80 (кг) -двайная маса малака

2) 80:2 = 40 (кг) - маса малака ў бідоне

3) 44-40 = 4 (кг) - маса пустога бідона

Спосаб 2 - ураўніванне па масе пустога бідона .

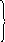
Б. - !---! ? кг 44-36(кг)

М.- !---!............36 кг...................! -? кг

1) 44-36 = 8 (кг)- двайная маса пустога бідона

2) 8 : 2 = 4 (кг) - маса пустога бідона

3) 44-4 = 40 (кг) - маса малака ў бідоне

Адказ: маса малака - 40кг, а бідона - 4 кг

Задача 2. Гарбуз у 3 разы цяжэйшы за дыню.

Іх агульная маса - 12кг. Якая маса гарбуза і дыні паасобку? Задачы 2, таксама 3 зручна рашаць на часткі з прымяненнем мадэлявання іх адрэзкамі.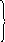

М.д. - !---! 1ч. 12 кг

М.г. - !---!---!---! 3ч.

1) 1+3=4 (ч.) складае маса дыні і гарбуза

2) 12:4=3 (кг)- маса дыні (1 частка)

3) 3·3= 9 (кг) - маса гарбуза (3 часткі)

Адказ: маса дыні 3кг, а гарбуза - 9кг.

Задача 3. Гарбуз у 3 разы або на 6 кг цяжэйшы за дыню. Якая маса дыні і гарбуза паасобку?

М.г. - !---!---!---! -?кг

М.д. - !---! 2ч. або 6 кг -?кг

1) 3 - 1 = 2 (ч.) складаюць 6 кг

2) 6 :2 = 3 (кг) - маса дыні (1 частка)

3) 3·3 = 9 (кг) - маса гарбуза (3 часткі)

Задача 4. Турыст на байдарцы праехаў шлях па цячэнню ракі са скорасцю 14 км/гадз., а супраць цячэння той жа шлях - са скорасцю 8 км/гадз. Якая скорасць цячэння ракі і скорасць руху байдаркі? Задача 4 рашаецца шляхам мадэлявання руху адрэкамі: па цячэнню ракі, калі прыбаўляецца скорасць цячэння да скорасці байдаркі, і супраць цячэння, калі аднімаецца скорасць цячэння ад скорасці байдаркі. З чарцяжу бачна, што пры складанні лікаў 14 і 8 атрымоўваецца двайная скорасць байдаркі, а пры адніманні гэтых лікаў двайная скорасць цячэння ракі. Адкуль існуюць два спосабы рашэння:

Спосаб 1:

1) (14+8):2=11(км/гадз.) - скорасць байдаркі 2) 14-11= 3 (км/гадз.) - скорасць цячэння ракі

Спосаб 2:

1) (14-8):2=3(км/гадз.)-скорасць цячэння ракі 2) 3+8= 11 (км/гадз)- скорасць байдаркі