Долгота осевого меридиана зоны с номером n равна:
0 = 6 N 3 .
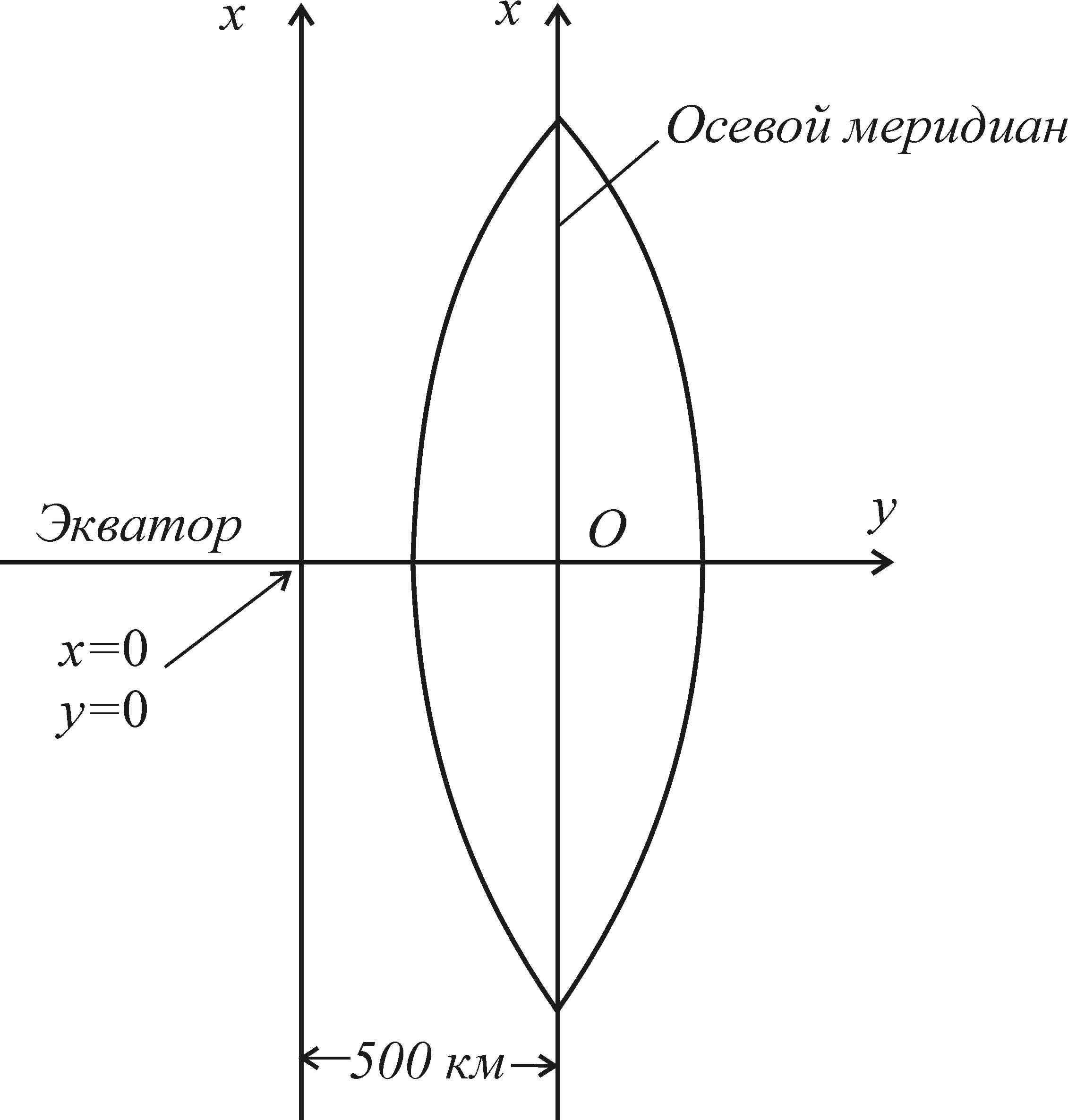
Осевой меридиан зоны и экватор изображаются на плоскости прямыми линиями (рис. 2.4). Осевой меридиан принимают за ось абсцисс x, а экватор за ось ординат y. Их пересечение (точка O) служит началом координат данной зоны.
|
|
Рис. 2.4. Изображение координатной зоны на плоскости: О– начало координат (х0=0;у0=500 км). |
Чтобы избежать отрицательных значений ординат, координаты пересечения принимают равными x0 = 0, y0 = 500 км, что равносильно смещению оси х к западу на 500 км.
Чтобы по прямоугольным координатам точки можно было судить, в какой зоне она расположена, к ординате y слева приписывают номер координатной зоны.
Пусть например, координаты точки А имеют вид:
xА = 6 276 427 м
yА = 12 428 566 м
Эти координаты указывают на то, что точка А находится на расстоянии 6276427 м от экватора, в западной части (y 500 км) 12-ой координатной зоны, на расстоянии 500000 428566 = 71434 м от осевого меридиана.
Для пространственных прямоугольных, геодезических и плоских прямоугольных координат в России принята единая система координат СК-95, закрепленная на местности пунктами государственной геодезической сети и построенная по спутниковым и наземным измерениям по состоянию на эпоху 1995 г.
Местные системы прямоугольных координат. При строительстве различных объектов часто используют местные (условные) системы координат, в которых направления осей и начало координат назначают, исходя из удобства их использования в ходе строительства и последующей эксплуатации объекта.
Так, при съемке железнодорожной станции ось у направляют по оси главного железнодорожного пути в направлении возрастания пикетажа, а ось х – по оси здания пассажирского вокзала.
При строительстве мостовых переходов ось х обычно совмещают с осью моста, а ось y идет в перпендикулярном направлении.
При строительстве крупных промышленных и гражданских объектов оси x и y направляют параллельно осям строящихся зданий.
4.Метод проекций в геодезии
 Пусть
многоугольник ABCDE
(рис.
2)
представляет
часть земной поверхности. Возьмем
плоскость PQ
и
опустим из каждой вершины многоугольника
перпендикуляры на эту плоскость.
Основания этих перпендикуляров обозначим
соответственно через а,
Ь, с, й, е. Порченные
на плоскости точки называются
ортогональны-м
и
(прямоугольными) проекция
м и точек пространства; линии
Пусть
многоугольник ABCDE
(рис.
2)
представляет
часть земной поверхности. Возьмем
плоскость PQ
и
опустим из каждой вершины многоугольника
перпендикуляры на эту плоскость.
Основания этих перпендикуляров обозначим
соответственно через а,
Ь, с, й, е. Порченные
на плоскости точки называются
ортогональны-м
и
(прямоугольными) проекция
м и точек пространства; линии
Плоский многоугольник abede является ортогональной проекцией пространственного многоугольника ABCDE.
Другая имеющая весьма важное значение в геодезии проекция называется центральной. Суть ее заключается в следующем. Возьмем произвольную точку О (рис. 3) и соединим ее со всеми вершинами многоугольника ABCDE, находящегося на земной поверхности. Полученные в пересечении с горизонтальной плоскостью PQ точки abede и будут центральными проекциями точек ABCDE,
Плоский многоугольник abode называется центральной проекцией многоугольника ABCDE.
5. Системы высот
Счет высот в инженерной геодезии ведут от одной из уровенных поверхностей.
Высотой точки называют расстояние по отвесной линии от точки до уровенной поверхности, принятой за начало счета высот.
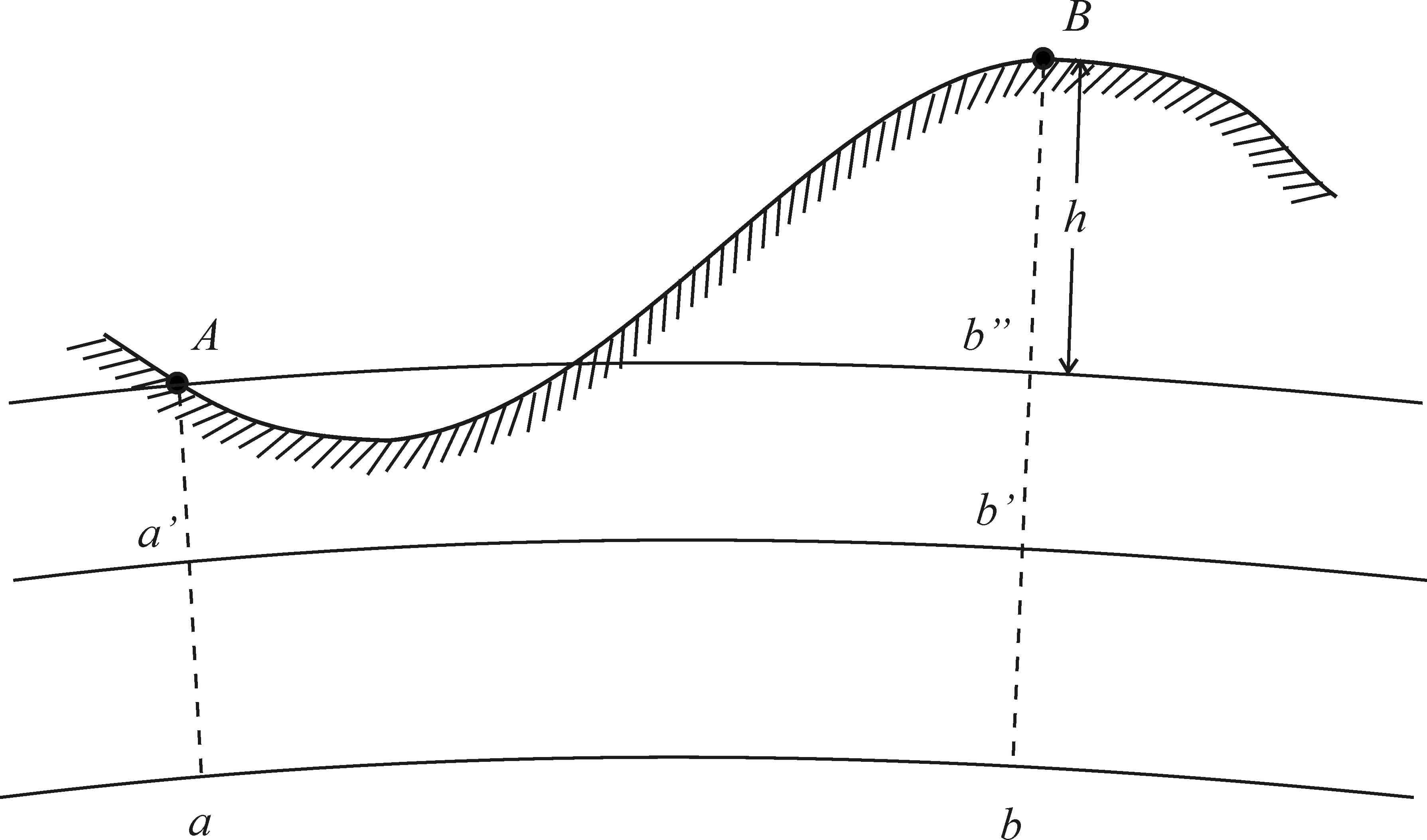
Если высоты отсчитывают от основной уровенной поверхности, то есть от поверхности геоида, их называют абсолютными высотами. На рис. 2.5 отрезки отвесных линий Аа и Вв абсолютные высоты точек А и В.
Если за начало счета высот выбрана какая-либо другая уровенная поверхность, то высоты называют условными. На рис. 2.5 отрезки отвесных линий Аа и Вв условные высоты точек А и В.
В России принята Балтийская система высот.Счет абсолютных высот ведут от уровенной поверхности, проходящей черезнуль Кронштадтского футштока.
Численное значение высоты принято называть отметкой. Например, если высота точкиАравна HА= 15,378 м, то говорят, что отметка точки равна 15,378 м.
|
|
Рис. 2.5. Абсолютные и условные высоты: ab– уровенная поверхность;ab–поверхность геоида;Ab– уровенная поверхность точкиA;
|
Разность высот двух точек называется превышением. Так, превышение точки В над точкой А равно
hAB = HВ HA.
Зная высоту точки А, для определения высоты точки В на местности измеряют превышение hAB. Высоту точки В вычисляют по формуле
HВ = HA + hAB.
Измерение превышений и последующее вычисление высот точек называется нивелированием.
Абсолютную высоту точки следует отличать от ее геодезической высоты, то есть высоты, отсчитываемой от поверхности земного эллипсоида (см. раздел 2.2). Геодезическая высота отличается от абсолютной высоты на величину отклонения поверхности геоида от поверхности эллипсоида.
В заключение отметим, что точное определение положения поверхности геоида в области материков невозможно. Поэтому принято отсчитывать высоты от близкой к геоиду, но доступной точному определению вспомогательной поверхности, названной квазигеоидом. Высоты, отсчитываемые от поверхности геоида, называются ортометрическими высотами, а отсчитываемые от поверхности квазигеоида – нормальными высотами. На результаты измерений, выполняемых в инженерной геодезии, различия в двух названных системах высот влияния не оказывают, и в дальнейшем мы их различать не будем, а будем пользоваться введенным выше обобщенным понятием – абсолютные высоты.