1.2 Лебегова мера плоских множеств

Элементарные множества не исчерпывают всех множеств, которые встречаются в геометрии и в классическом анализе. Поэтому естественно попытаться распространить понятие меры, с сохранением ее основных свойств, на класс множеств более широкий, чем конечные объединения прямоугольников со сторонами, параллельными осям координат.

Решение этой задачи, в известном смысле окончательное, было дано Анри Леоном Лебегом в начале XX века. [6]

При изложении теории меры Лебега нам придется рассматривать не только конечные, но и бесконечные объединения прямоугольников. Для того чтобы при этом сразу же не столкнуться с множествами «бесконечной меры», ограничимся сперва множествами, целиком принадлежащими квадрату

На совокупности всех таких множеств определим функцию μ* (A) следующим образом.

Определение 1. [5] Внешней мерой множества А называется число ,где нижняя грань берется по всевозможным покрытиям множества А конечными или счетными системами прямоугольников.

Замечание 1. Если бы мы в определении внешней меры рассматривали покрытия, состоящие не только из прямоугольников, но из любых элементарных множеств (взятых в конечном или счетном числе), то мы получили бы, очевидно, тоже самое значение μ* (А), поскольку всякое элементарное множество есть сумма конечного числа прямоугольников.

Замечание 2. Если А — элементарное множество, то μ* (А) = m'(А). Действительно, пусть P₁, ... , Рn — составляющие А прямоугольники.

Тогда, по определению, .Так как прямоугольники Pi покрывают А, то .

Но если {Qj} — произвольная конечная или счетная система прямоугольников, покрывающая А, то в силу теоремы 2 поэтому

Теорема 3. [5] Если ,где Аn — конечная или счетная система множеств, то (2)

В частности, если А В, то

Доказательство. По определению внешней меры, для каждого Аn найдется такая система прямоугольников {Рnk}, конечная или счетная, что и ,где ε > 0 выбрано произвольно. Тогда

Поскольку ε> 0 произвольно, отсюда вытекает утверждение теоремы.

Так как на элементарных множествах m’ и μ* совпадают, то теорема 2 представляет собой частный случай теоремы 3.

Определение 2. Множество А называется измеримым (в смысле Лебега), если для любого ε> 0 найдется такое элементарное множество В. что .

Функция μ*, рассматриваемая только на измеримых множествах, называется лебеговой мерой. Будем обозначать ее через μ.

Замечание. [6] Введенное нами определение измеримости имеет достаточно наглядный смысл. Оно означает, что множество измеримо, если его можно «сколь угодно точно приблизить» элементарными множествами.

Итак, мы определили некоторый класс множеств, называемых измеримыми, и функцию μ, меру Лебега, на этом классе. Наша ближайшая цель — установить следующие факты:

1. Совокупность измеримых множеств замкнута относительно операций взятия конечных или счетных сумм и пересечений.

2. Функция μ Ϭ-аддитивна на .

Нижеследующие теоремы представляют собой этапы доказательства этих утверждений.

Теорема 4. Дополнение измеримого множества измеримо.

Это сразу следует из равенства (Е \ А) (Е \ В) = А В, которое проверяется непосредственно.

Теорема 5. [5] Сумма и пересечение конечного числа измеримых множеств суть измеримые множества.

Доказательство. Достаточно провести доказательство для двух множеств. Пусть А₁ и А₂ — измеримые множества. Это значит, что для любого еε> 0 найдутся такие элементарные множества В₁ и B₂, что

Так как ,то

Но В₁UB₂ — элементарное множество, поэтому множество A₁UА₂ измеримо.

Измеримость пересечения двух измеримых множеств вытекает из теоремы 4 и соотношения (4)

Следствие. Разность и симметрическая разность двух измеримых множеств измеримы.

Это вытекает из теорем 4 и 5 и равенств

Теорема 6. Если попарно непересекающиеся измеримые множества, то (5)

Для доказательства этой теоремы нам понадобится следующая лемма.

Лемма. Для любых двух множеств А и В

Доказательство леммы. Так как то в силу теоремы 3

Отсюда вытекает утверждение леммы в случае μ*(А) μ*(В). Если же μ*(А) μ*(B), то утверждение леммы вытекает из неравенства устанавливаемого аналогично.

Доказательство теоремы 6. Как и в теореме 5, достаточно рассмотреть случай двух множеств. Выберем произвольное ε > 0 и такие элементарные множества В₁ и В₂, что

(6)

(7)

Положим и . Множество А измеримо в силу теоремы 5. Так как множества А₁ и А₂ не пересекаются, то

и, следовательно, (8)

В силу леммы из (6) и (7) вытекает, что

(9)

(10)

Так как на совокупности элементарных множеств мера аддитивна, то из (8)-(10) получаем

Заметив еще, что имеем, наконец,

Так как ε > 0 может быть выбрано произвольно малым, то .Поскольку противоположное неравенство справедливо (в силу теоремы 3) всегда, окончательно получаем так как А₁, А₂ и А измеримы, то здесь μ* можно заменить на μ. Теорема доказана.

Из этой теоремы, в частности, следует, что для всякого измеримого А

Теорема 7. Сумма и пересечение счетного числа измеримых множеств суть измеримые множества.

Доказательство. Пусть - счетная система измеримых множеств и . Положим .

Ясно, что, причем множества Аnпопарно не пересекаются. В силу теоремы 5 и следствия из нее все множества А'n измеримы. В силу теоремы 6 и определения внешней меры при любом конечном n поэтому ряд сходится и, следовательно, для любого ε > 0 найдется такое N, что .(11)

Так как множество измеримо (как сумма конечного чиcла измеримых множеств), то для него найдется такое элементарное множество В, что (12)

Поскольку ,то из (11) и (12) вытекает ,

т. е. А измеримо.

Так как дополнения измеримых множеств измеримы, то утверждение теоремы относительно пересечений вытекает из равенства

Теорема 7 усиливает теорему 5. Следующая теорема представляет собой аналогичное усиление теоремы 6.

Теорема 8. [5] Если {Аn}—последовательность попарно непересекающихся измеримых множеств и , то

Доказательство. В силу теоремы 6 при любом N

Переходя к пределу при , получаем

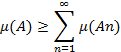(13)

С другой стороны, согласно теореме 3 (14)

Из (13) и (14) вытекает утверждение теоремы.

Установленное в теореме 8 свойство меры было названо ее счетной аддитивностью, или Ϭ- аддитивностью. Из Ϭ-аддитивности вытекает следующее свойство меры, называемое непрерывностью.

Теорема 9. Если -последовательность вложенных друг в друга измеримых множеств и , то

Доказательство. Достаточно рассмотреть случай А =; общий случай сводится к этому заменой Аn на An \ А. Имеем

причем слагаемые не пересекаются. Поэтому, в силу Ϭ-аддитивности μ

(15)

(16)

так как ряд (15) сходится, то его остаток (16) стремится к 0 при . Таким образом, при , что и требовалось доказать.

Следствие. Если - возрастающая последовательность измеримых множеств и ,то

Для доказательства достаточно перейти от множеств Аn к их дополнениям и воспользоваться теоремой 9. [5]

Отметим в заключение еще одно очевидное, но важное обстоятельство. Всякое множество А, внешняя мера которого равна 0, измеримо. Достаточно положить В = ; тогда

Итак, мы распространили меру с элементарных множеств на более широкий класс , замкнутый относительно операций взятия счетных сумм и пересечений, т. е. представляющий собой Ϭ-алгебру.

Построенная мера Ϭ-аддитивна на этом классе. Установленные выше теоремы позволяют составить следующее представление о совокупности измеримых по Лебегу множеств.

Всякое открытое множество, принадлежащее Е, можно представить как объединение конечного или счетного числа открытых прямоугольников, т. е. измеримых множеств, и в силу теоремы 7 все открытые множества измеримы. Замкнутые множества суть дополнения открытых, следовательно, они тоже измеримы. Согласно теореме 7 измеримыми должны быть и все те множества, которые могут быть получены из открытых и замкнутых с помощью конечного или счетного числа операций взятия счетных сумм и пересечений.

Можно показать, однако, что этими множествами все измеримые множества еще не исчерпываются.