Глава 1 теоретические аспекты, касающиеся меры лебега

1. Мера элементарных множеств

Воспользовавшись научными выводами А.Н. Колмогорова [5] сформулируем основные и свойства меры Лебега.

Рассмотрим систему Ϭ множеств на плоскости (х,у), каждое из которых определяется одним из неравенств вида

и одним из неравенств вида

где а, b, с и d — произвольные числа. Множества, принадлежащие этой системе, мы будем называть прямоугольниками. Замкнутый прямоугольник, определяемый неравенствами

представляет собой прямоугольник в обычном смысле (вместе с границей), если а < d и с < d, отрезок (если а = b и с < d или а < b и с = d), точку (при а = b, с = b) и, наконец, пустое множество (если а >b или с > d). Открытый прямоугольник

будет в зависимости от соотношений между а, b, с и d прямоугольником без границы или пустым множеством. Каждый из прямоугольников остальных типов (назовем их полуоткрытыми) представляет собой настоящий прямоугольник без одной, двух или трех сторон, интервал, полуинтервал, либо, наконец, пустое множество.

Класс всех прямоугольников на плоскости обозначим Ϭ.

Для каждого из прямоугольников определим его меру в соответствии с известным из элементарной геометрии понятием площади.

Именно:

а) мера пустого множества равна 0;

б) мера непустого прямоугольника (замкнутого, открытого или полуоткрытого), определяемого числами а, b, с и d, равна .

Таким образом, каждому прямоугольнику Р из Ϭ поставлено в соответствие число т(Р) — его мера; при этом выполнены следующие условия:

1) мера ᶆ(Р) принимает действительные неотрицательные значения;

2) мера ᶆ (Р) аддитивна, т.е. если и при , то

Наша задача — распространить, с сохранением свойств 1) и 2), меру m(Р), определенную пока для прямоугольников, на более широкий класс множеств.

Сначала мы распространим меру на так называемые элементарные множества. Назовем плоское множество элементарными, если его можно представить хотя бы одним способом как объединение конечного числа попарно непересекающихся прямоугольников.

Для дальнейшего нам понадобится следующая теорема.

Теорема 1. [1] Объединение, пересечение, разность и симметрическая разность двух элементарных множеств также являются элементарными множествами.

Доказательство. Ясно, что пересечение двух прямоугольников есть снова прямоугольник. Поэтому, если , два элементарных множества, то и их пересечение — элементарное множество.

Разность двух прямоугольников есть, как легко проверить, элементарное множество. Следовательно, вычитая из прямоугольников некоторое элементарное множество, мы снова получим элементарное множество (как пересечение элементарных). Пусть теперь множества А и В — элементарные. Найдется, очевидно, прямоугольник Р, содержащий каждое из них. Тогда множество в силу сказанного выше будет элементарным. Отсюда и из равенств ,следует, что разность и симметрическая разность элементарных множеств являются элементарными множествами. Теорема доказана.

Определим теперь меру m'(А) для элементарных множеств следующим образом: если ,где Pk - попарно непересекающиеся прямоугольники, то .

Покажем, что m'(А) не зависит от способа разложения А в сумму конечного числа прямоугольников. Пусть ,где Pk и Qj — прямоугольники, и при . Так как пересечение двух прямоугольников есть прямоугольник, то, в силу аддитивности меры для прямоугольников,

В частности, для прямоугольников мера m' совпадает с исходной мерой m.

Легко видеть, что определенная таким образом мера элементарных множеств неотрицательна и аддитивна.

Установим следующее важное свойство меры элементарных множеств.

Теорема 2. [1] Если А — элементарное множество и {Аn} — конечная или счетная система элементарных множеств такая, что то, (1)

Доказательство. Для любого ε > 0 и данного А можно, очевидно, найти такое замкнутое элементарное множество А, которое содержится в А и удовлетворяет условию

(Достаточно каждый из к составляющих А прямоугольников Pi заменить лежащим внутри него замкнутым прямоугольником с площадью большей, чем )

Далее, для каждого Аn можно найти открытое элементарное множество Аn, содержащее Аn и удовлетворяющее условию .Ясно, что .Из {Аn} можно (по лемме Гейне-Бореля) выбрать конечную систему , покрывающую А. При этом, очевидно, (так как иначе А оказалось бы покрытым конечным числом прямоугольников, суммарной площади меньшей, чем m'(А), что невозможно). Поэтому

откуда в силу произвольности > 0 вытекает (1).

Свойство меры m', устанавливаемое теоремой 2 (мера множеств не превосходит суммы мер покрывающих его множеств, взятых в конечном или счетном числе), называется полуаддитивностью. Из него вытекает свойство так называемой счетной аддитивности, или Ϭ - аддитивности, состоящее в следующем.

Пусть элементарное множество А представлено как сумма счетного числа непересекающихся элементарных множеств Аn (n= 1,2,...): ,тогда (т. е. мера суммы счетного числа непересекающихся слагаемых равна сумме мер).

Действительно, в силу аддитивности при любом N имеем:

Переходя к пределу при N , получаем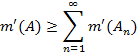

В силу теоремы 2 имеет место и противоположное неравенство. Таким образом, Ϭ - аддитивность меры m’ доказана.