§ 8. Прямая и плоскость

Задача. Найти точку пересечения прямой и плоскости:

Решение. Запишем параметрические уравнения прямой: подставим эти значения координат в уравнение плоскости:Подставляяв параметрические уравнения, получим координаты точки пересечения:

Ответ: М(2;-3;6).

Задача. Найти проекцию точки Р(2;-1;3) на прямую

Решение. Через точку Р проведем плоскость , перпендикулярную прямойL; навправляющий вектор прямой будет являться нормалью плоскости. Используя уравнение (1) § 6, имеем:

Проекцией точки Р на прямую L, таким образом, является точка пересечения прямой и плоскости:

Точка О(3;-2;4) – искомая проекция.

Задача. Вычислить расстояние d от точки Р(2;3;-1) до прямой

.

Р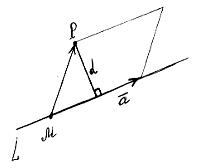ешение. Выберем на прямой L произвольную точку, например М(5;0;-25); будем считать, что направляющий вектор прямой приложен в точкеМ. Соединим точки М и Р и достроим фигуру до параллелограмма; его высота, проведенная из вершины Р, будет являться искомым расстоянием d: где— длина векторного произведения, определяющая площадь параллелограмма, построенного на векторахиВычислим координаты вектора:найдем векторное произведение:

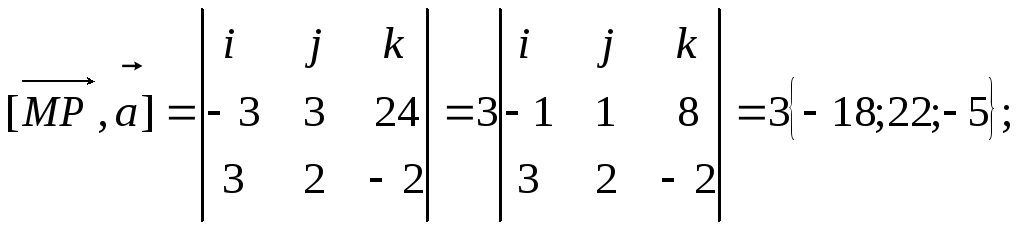
определим его модуль:

длина вектора

Найдем искомое расстояние:

Ответ: 21.

Задача. Вычислить кратчайшее расстояние между двумя прямыми

и

Решение. Определим взаимное расположение прямых L₁ и L₂. Они непараллельны, т.к. неколлинеарны векторы иПроверим,илиL₁ и L₂ скрещивающиеся; для этого выпишем найдем вектори вычислим определитель из равенства (7)§ 7:

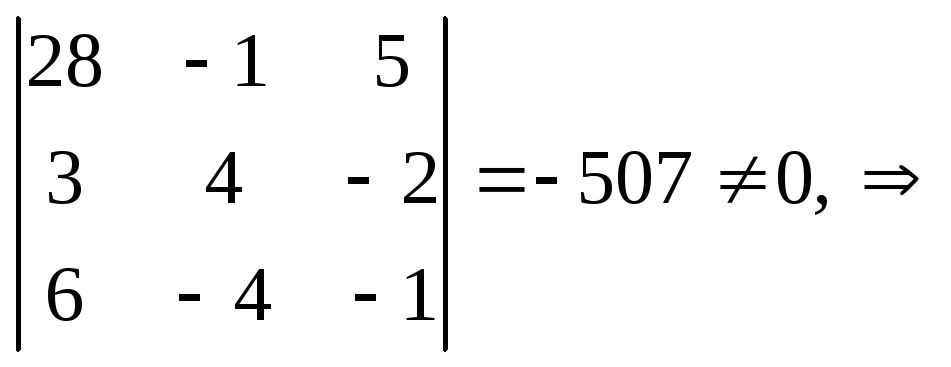L₁ и L₂ – скрещивающиеся.

Расстоянием d между скрещивающимися прямыми L₁ и L₂ будет являться высота параллелепипеда, построенного на векторах

т.е.

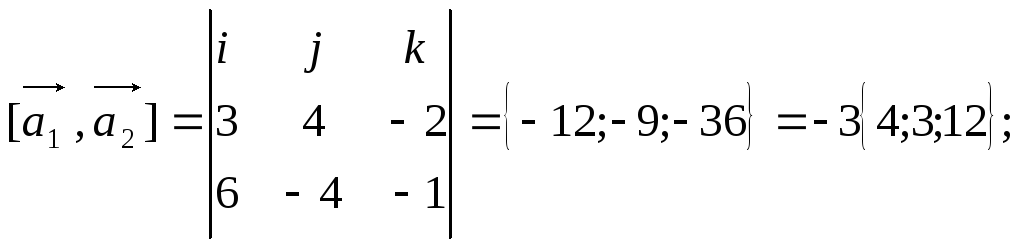
Таким образом,

Задачи для самостоятельного решения.

1. Найти точку пересечения прямой и плоскости:

1)

2) (Ответ: 1) прямая паралле-льная плоскости; 2) прямая лежит на плоскости)

2. Составить канонические уравнения прямой, проходящей через точку М₀(2;-4;-1) и середину отрезка прямой заключенного между плоскостями(Ответ:)

3. При каких значениях A и D прямая лежит в плоскости(Ответ:А=3, D=-23)

4. При каких значениях иС прямая перпендикулярна к плоскости(Ответ:)

5. Найти точку Q, симметричную точке Р(4;1;6) относительно прямой

, (Ответ: Q(2;-3;2))

6. Найти проекцию точки Р(5;2;-1) на плоскость (Ответ:(1;4;-7))

7. Найти точку Q, симметричную точке Р(1;3;-4) относительно плоскости (Ответ:Q(-5;1;0))

8. Вычислить расстояние d от точки Р(2;3;-1) до прямых:

1) ;

2) (Ответ: 1)6; 2) 15).

9. Убедившись, что прямые параллельны, вычислить расстояниеd между ними. (Ответ: d =25)

10. Написать уравнение плоскости, которая проходит через точку М₀(3;1;-2) и через прямую (Ответ:)

11. Через прямую провести плоскость, перпенди-кулярную к плоскости(Ответ:)

12. Найти проекцию прямой на плоскость. (Ответ:)

13. Проверить, что прямые ипересекаются, и написать уравнение плоскости, через них проходящей. (Ответ:)

14. Провести плоскость через перпендикуляры, опущенные из точки Р(-3;2;5) на плоскости: и

(Ответ: )

15. Даны вершины треугольника А(4;1;-2), В(2;0;0), С(-2;3;-5). Составить уравнения его высоты, опущенной из вершины В на противолежащую сторону. (Ответ: )