§ 7. Прямая в пространстве.
Прямая в пространстве задается несколькими способами.
1. Прямая как линия пересечения двух плоскостей:
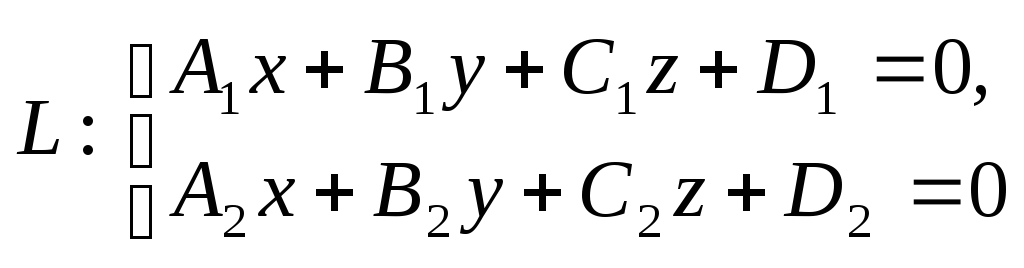(1)
при условии, что коэффициенты А1, В1, С1 непропорциональны коэффициентам А2, В2, С2.
Уравнение
(2)
называется уравнением пучка плоскостей.
2. Канонические уравнения прямой:
, (3)
где
точка М0(x0;y0;z0)
— точка прямой;
—
направляющий вектор прямой.
3. Уравнения прямой, проходящей через две точки M1(x1;y1;z1) и M2(x2;y2;z2):
(4)
4. Параметрические уравнения прямой:
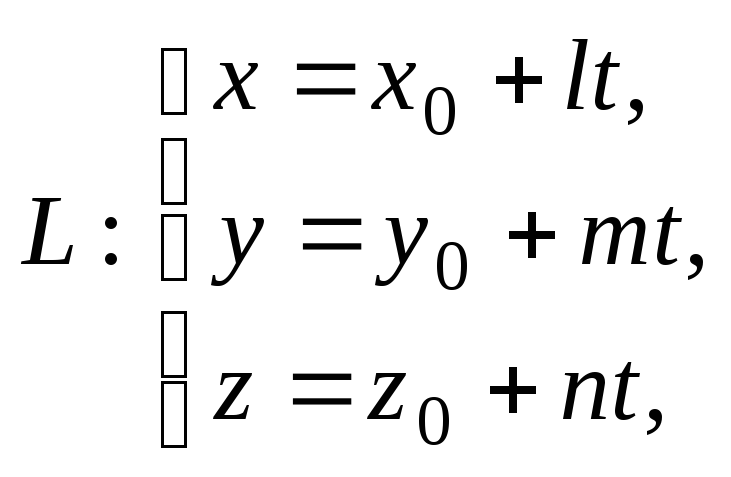(5)
где t — произвольно изменяющийся параметр.
Угол
между
двумя прямыми
и
равен
углу между их направляющими векторами
и
,
т.е. имеет место формула:
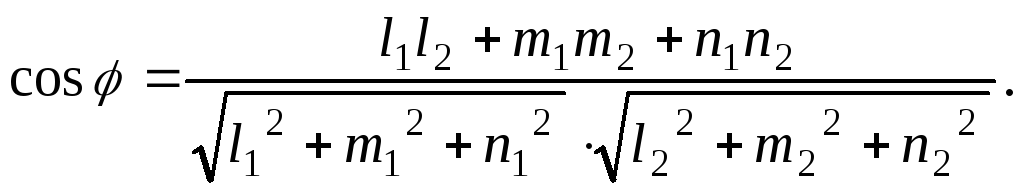(6)
Условие, при котором прямые L1 и L2 лежат в одной плоскости:
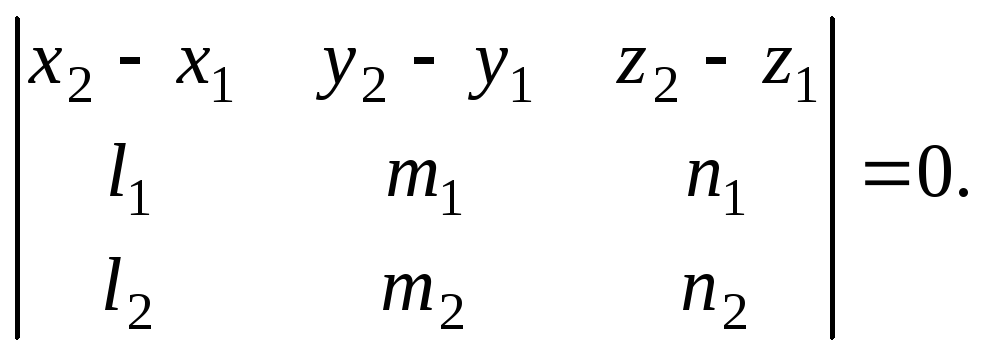(7)
Следовательно, прямые скрещиваются, если равенство (7) не имеет место.
Рассмотрим задачи.
Задача.
Составить уравнение плоскости
,
проектирующей прямую
на плоскость
Решение.
Искомая плоскость
проходит через линию пересеченияL
перпендикулярно к плоскости
.
Составим уравнение пучка плоскостей:
Обозначим
через
и
нормали
плоскостей
и
соответственно.
Тогда:
Найдем
числа
и
,
учитывая, что
т.е.
Пусть
тогда
Подставив эти значения в уравнение
пучка, получим:
Задача. Составить канонические и параметрические уравнения прямой
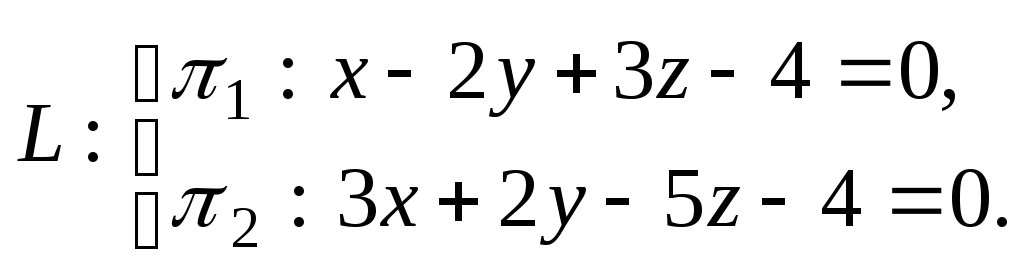
Решение.
Чтобы перейти к каноническому и
параметрическому заданиям прямой L
зафиксируем
на ней произвольную точку М0
и найдем ее направляющий вектор в виде:
.
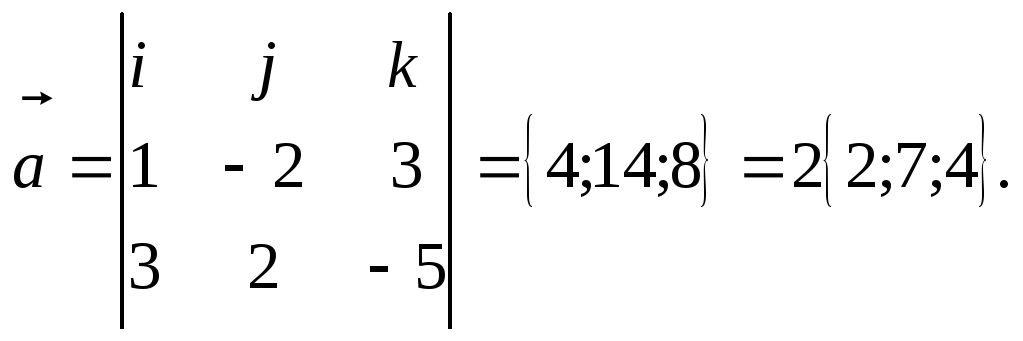
Пусть М0(х;у;0), тогда получим:
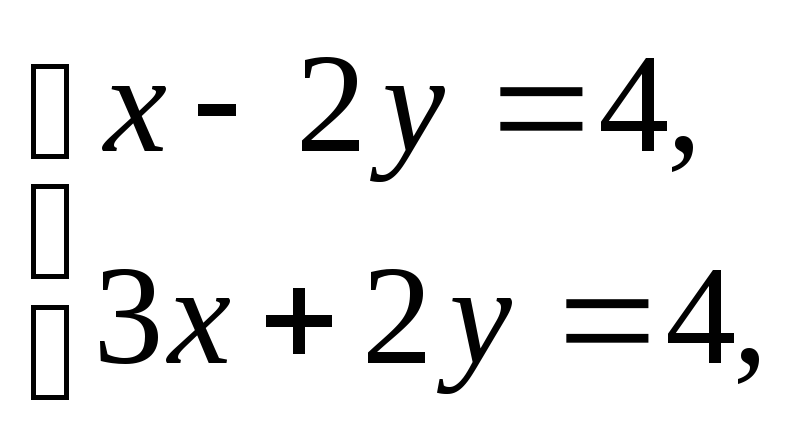
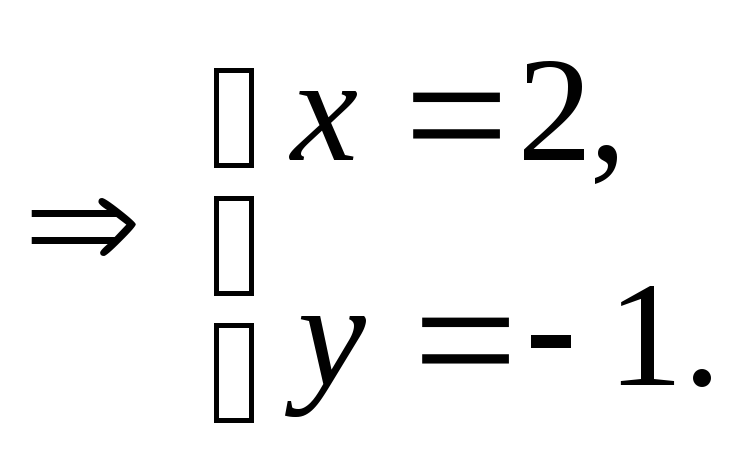
Т.е.
Искомые
уравнения: 
или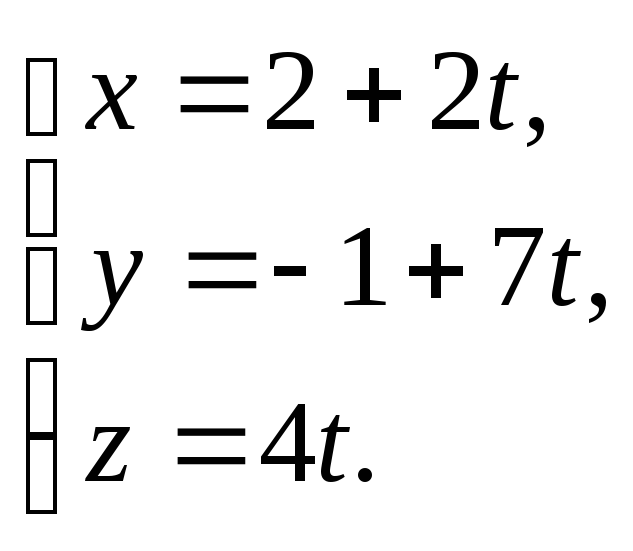
Задача.
Составить уравнения прямой L1,
которая проходит через точку М1(-1;2;-3)
перпендикулярно к вектору
и
пересекает прямую
.
Решение.
Канонические уравнения искомой прямой
.
Найдем ее направляющий вектор
;
для этого решим систему, первое уравнение
которой вытекает из перпендикулярности
векторов
и
,
а второе — из равенства (7):
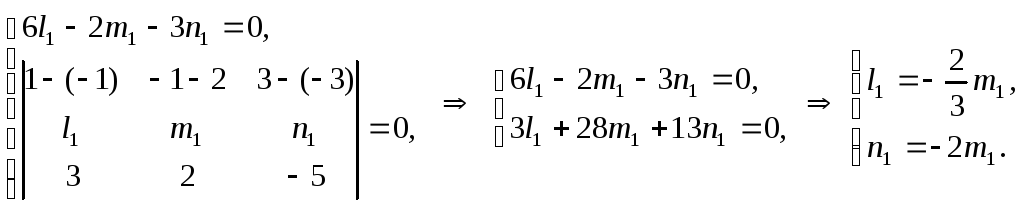
Пусть
Тогда
Таким
образом,
Задачи для самостоятельного рассмотрения.
1.
Составить уравнения прямой, образованной
пересечением плоскости 3x-y-7z+9=0
с плоскостью, проходящей через ось Ох
и точку Е(3;2;-5).
(Ответ:
)
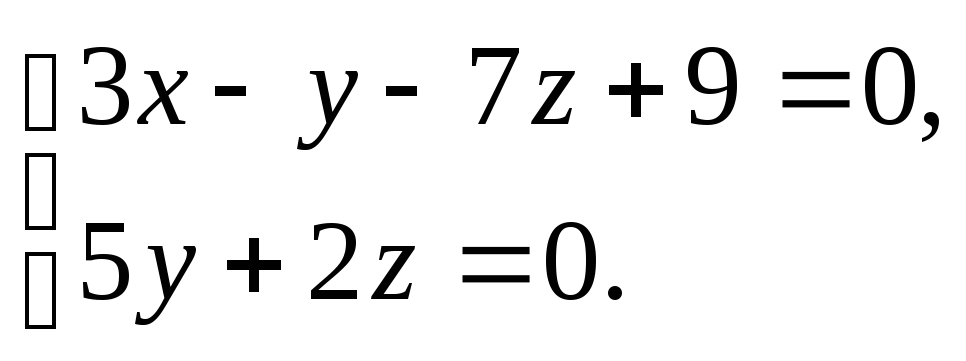2.
Составить уравнение плоскости, проходящей
через прямую пересечения плоскостей
параллельно вектору
(Ответ:
)
3.
Составить уравнение плоскости, проходящей
через прямую пересечения плоскостей
перпендикулярно
плоскости
(Ответ:
)
4.
Написать уравнение плоскости, которая
принадлежит пучку плоскостей
и
отстоит от точкиС(3;-2;-3)
на расстояние d=7.
(Ответ:
)
5.
Составить уравнения плоскостей,
проектирующих прямую
на координатные плоскости.
(Ответ:
)
6.
Составить уравнения прекции прямой
на плоскость
(Ответ:
)
7.
Составить канонические и параметрические
уравнения прямой, проходящей через
точку М(2;0;-3)
параллельно: 1) вектору
2) прямой
3) осиОх.
(Ответ:
1)
2)
3)
)
8.
Даны вершины треугольника А(3;6;-7),
В(-5;2;3)
и С(4;-7;-2).
Составить параметрические уравнения
его медианы, проведенной из вершины С.
(Ответ:
)
9.
Даны вершины треугольника А(3;-1;-1),
В(1;2;-7)
и С(-5;14;-3).
Составить канонические уравнения
биссектрисы его внутреннего угла при
вершине С.
(Ответ:
)
10.
Составить канонические уравнения
прямой, проходящей через точку М(2;3;-5)
параллельно прямой:
(Ответ:
)
11. Доказать параллельность прямых:
1)
и
2)
и
3)
и
12. Доказать перпендикулярность прямых:
1)
и
2)
и
3)
и
13.
Найти острый угол между прямыми
(Ответ: 60о)
14. Составить уравнения прямой, которая проходит через точку
М1(-4;-5;3) и пересекает две прямые:
,
.
(Ответ:
)