§ 6. Плоскость в пространстве

Уравнение (1) определяет плоскость, проходящую через точкуM₀(x₀;y₀;z₀) и имеющую нормаль .

Уравнение (1) представим в виде:

(2) где.

Уравнение (2) называется общим уравнением плоскости.

Уравнение плоскости, проходящей через точку M₀(x₀;y₀;z₀) параллельно векторам и:

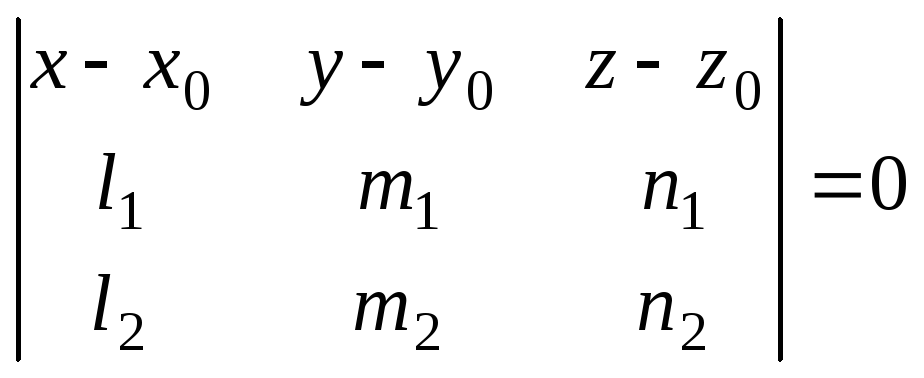. (3)

Уравнение плоскости, проходящей через точки M₁(x₁;y₁;z₁) и M₂(x₂;y₂;z₂) параллельно вектору :

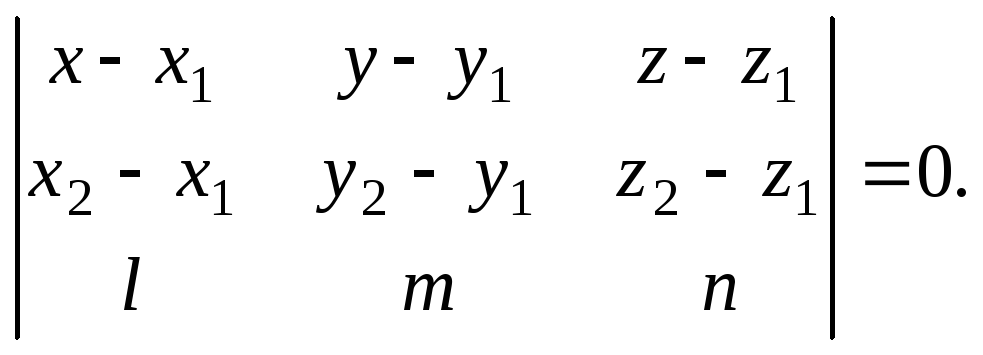(4)

Уравнение плоскости, проходящей через точки M₁(x₁;y₁;z₁), M₂(x₂;y₂;z₂) и M₃(x₃;y₃;z₃):

(5)

Уравнение плоскости «в отрезках»:

(6) где― отрезки, отсекаемые плоскостью на координатных осях (считая от начала координат).

Нормальным уравнением плоскости называется уравнение вида:

(7)

где - направляющие косинусы нормали плоскости,р – расстояние от начала координат до плоскости.

Общее уравнение плоскости приводится к нормальному виду (7) умножением на нормирующий множитель, определяемый формулой:

(8)

знак нормирующего множителя берется противоположным знаку свободного члена D.

Отклонение точкиот плоскости дается формулой:

(9)

или (10)

Расстояние от точкиM^* до плоскости: , или

(11)

Угол между двумя плоскостями A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0 определяется по формуле:

,

или , (12)

где .

Условие параллельности двух плоскостей:

(13)

Условие перпендикулярности двух плоскостей:

(14)

Рассмотрим задачи.

Задача. Составить уравнение плоскости, которая проходит через точку М(2;-1;1) перпендикулярно к двум плоскостям 2x-z+1=0, y=0.

Решение. Т.к. искомая плоскость (обозначим ее через ) проходит перпендикулярно двум данным плоскостями, то нормали этих плоскостейипараллельны плоскости. Выпишем координатыи:

Составим уравнение плоскости , используя (3):

Задача. Вывести уравнение геометрического места точек, отклонение которых от плоскости 6x+3y+2z-10=0 равно –3.

Решение. Пусть– точка искомого множества точек; по условию задачи:

Получим: – уравнение плоскости, параллельной данной.

Задачи для самостоятельного решения.

1. Определить, при каких значениях иследующие пары уравнений будут определять параллельные плоскости: 1)2x+ly+3z-5=0, mx-6y-6z+2=0; 2)3x-y+lz-9=0, 2x+my+2z-3=0;

(Ответ: )

2. Определить двугранные углы, образованные пересечением следующих пар плоскостей: 1)

2) 3)

(Ответ: 1) и2)и3))

3. Составить уравнение плоскости, которая проходит через точку М₁(3;-2;-7) параллельно плоскости . (Ответ:)

4. Составить уравнение плоскости, которая проходит через две точки М₁(1;-1;-2) и М₂(3;1;1) перпендикулярно к плоскости . (Ответ:)

5. Определить, при каких значениях a и b плоскости 2x-y+3z-1=0, x+2y-z+b=0, x+ay-6z+10=0: 1) имеет одну общую точку; 2) проходят через одну прямую; 3) пересекаются по трем различным параллельным прямым. (Ответ: 1) )

6. Составить уравнение плоскости, которая проходит:

1) через точку М₁(2;-3;3) параллельно плоскости Оху;

2) через ось Oz и точку М₂(3;-4;7);

3) через точки Р₁(2;-1;1) и Р₂(3;1;2) параллельно оси Оу. (Ответ: 1) z-3=0; 2) 4x+3y=0; 3) x-z-1=0)

7. Вычислить площадь треугольника, который отсекает плоскость 5x-6y+3z+120=0 от координатного угла Оху. (Ответ: 240 кв. ед.)

8. Вычислить объем пирамиды, ограниченной плоскостью 2x-3y+6z-

-12=0 и координатными плоскостями. (Ответ: 8 куб. ед.)

9. Составить уравнение плоскости, которая проходит через точки М₁(-1;4;-1), М₂(-13;2;-10) и отсекает на осях абсцисс и аппликат отличные от нуля отрезки одинаковой длины.

(Ответ: 2x-21y+2z+88=0; 2x-3y-2z+12=0)

10. Вычислить расстояние между параллельными плоскостями:

1) x-2y-2z-12=0, x-2y-2z-6=0; 2) 2x-3y+6z-14=0, 4x-6y+12z+21=0;

3)16x+12y-15z+50=0, 16x+12y-15z+25=0; 4) 2x-y+2z+9=0, 4x-2y+4z-21=0. (Ответ: 1) 2; 2) 3,5; 3) 1; 4) 6,5)

11. На оси Oz найти точку, равноудаленную от точки М(1;-2;0) и от плоскости 3x-2y+6z-9=0. (Ответ: )

12. Составить уравнения плоскостей, параллельных плоскости 2x-2y-z-3=0 и отстоящих от нее на расстояние d=5. (Ответ: 2x-2y-z-18=0; 2x-2y-z+12=0)

13. Составить уравнение геометрического места точек, равноудаленных от двух параллельных плоскостей: 1) 4x-y-2z-3=0, 4x-y-

-2z-5=0; 2) 5x-3y+z+3=0, 10x-6y+2z+7=0. (Ответ: 1) 4x-y-2z-4=0;

2) 20x-12y+4z+13=0)

14. Составить уравнения плоскостей, которые делят пополам двугранные углы, образованные двумя пересекающимися плоскостями: 1) x-3y+2z-5=0, 3x-2y-z+3=0; 2) 5x-5y-2z-3=0, x+7y-2z+1=0).

(Ответ: 1) 4x-5y-z-2=0, 2x+y-3z+8=0; 2) x-3y-1=0, 3x+y-2z-1=0)

15. Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 2x-y+2z-3=0, 3x+2y-6z-1=0, в котором лежит точка М(1;2;-3). (Ответ: 23x-y-4z-24=0)