§ 5. Прямая на плоскости

Уравнение вида (1) называется уравнением прямой, проходящей через точкуи имеющейнормаль (нормаль или нормальный вектор — это вектор, перпендикулярный прямой).

Уравнение (1) приводится к общему уравнению прямой:

, (2)

где .

Уравнение прямой, проходящей через точку и имеющей угловой коэффициент:

, (3)

где (— угол наклона прямой к оси Ох).

Уравнение прямой c угловым коэффициентом:

(4)

где — величина отрезка, который прямая отсекает на оси Оу, считая от начала координат.

Уравнение прямой, проходящей через две точки точки и:

, (5)

или

, (6)

где — направляющий вектор прямой; (6) – каноническое уравнение прямой.

Угловой коэффициент прямой (5) вычисляется по формуле:

. (7)

Один из углов между двумя прямыми вычисляется по формуле:

, (8)

где и— угловые коэффициенты прямых.

Условие параллельности двух прямых:

. (9)

Условие перпендикулярности прямых:

, или . (10)

Если ни один из коэффициентов уравнения (2) не равен нулю, то его можно преобразовать к виду:

, (11)

где — величины отрезков, отсекаемых прямой на координатных осяхОх и Оу соответственно. Уравнение (11) называется уравнением прямой в «отрезках».

Нормальное уравнение прямой имеет вид:

(12)

где p — длина нормали, опущенной из начала координат на данную прямую; — угол между нормалью и осьюОх.

Уравнение (2) можно привести к уравнению (12); для этого его нужно умножить на нормирующий множитель :

(13)

Знак нормирующего множителя выбирается противоположным знаку свободного члена С уравнения (2).

Пусть дана какая-нибудь прямая l и произвольная точка ― расстояние от точкидо прямойl. Отклонением точкиот прямойl называется число , если точкаи начало координат лежат по разные стороны от прямойl, и , еслии начало координат расположены по одну сторону от прямойl (если , то). Отклонениевычисляется по формуле:

(14)

или

. (15)

Чтобы найти расстояние d от точки до прямой, нужно вычислить отклонение и взять его модуль: , т.е.

. (16)

Совокупность прямых, проходящих через некоторую точку S, называется пучком прямых с центром S.

Если и- уравнения двух прямых, пересекающихся в точкеS, то уравнение

(17)

где ― любые числа, не равные одновременно нулю, определяет прямую, также проходящую через точкуS. Уравнение (17) ― уравнение пучка прямых (с центром в точке S).

Рассмотрим задачи.

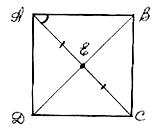
Задача. Точка E(1;-1) является центром квадрата, одна из сторон которого лежит на прямой Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.

Решение. Пусть сторона . ДиагоналиAC и BD являются биссектрисами углов квадрата. Используя формулу (8), найдем угловой коэффициент одной из диагоналей:

;;.

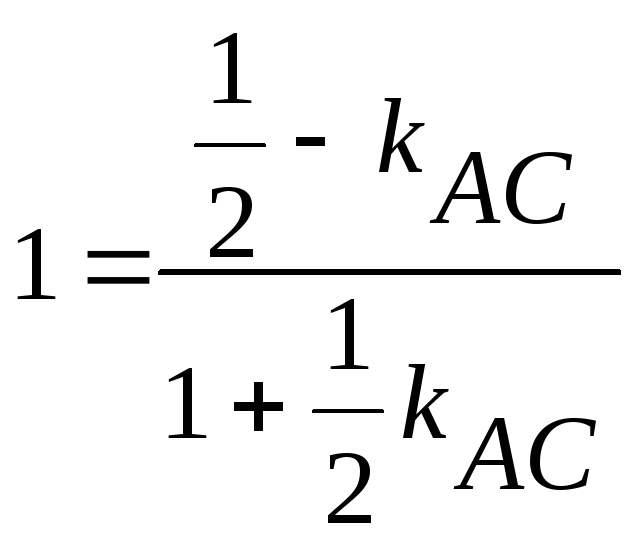Зная , точкуи применив (3), найдем уравнение диагоналиАС: ;

Решив систему уравнений прямых АВ и АС, найдем вершину А:

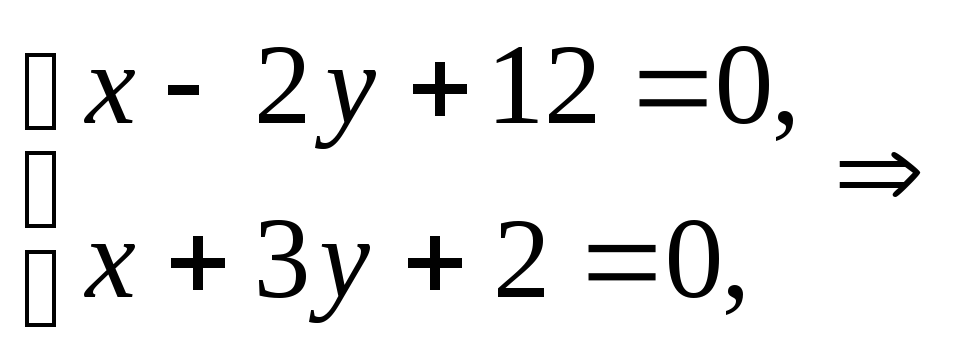
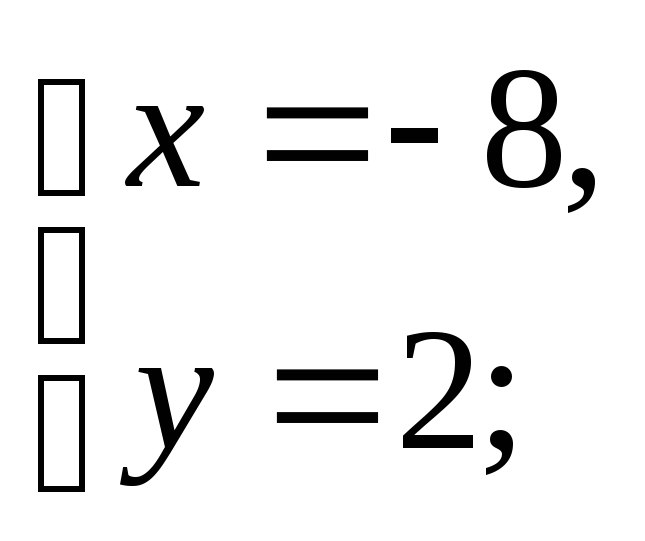т.е. А(-8;2).

Т.к. , то, согласно (10),следовательно,

Точка Е является серединой АС. Используем формулу (11) из § 2 :

.

Выражаем :,; т.е.С(10;-4).

(опираясь на (9)); найдем уравнение DC:

, .

Аналогично, ВС: ,.

Ответ: .

Задача. Составить уравнение сторон треугольника, зная одну его вершину В(2;6), а также уравнения высоты и биссектрисы, проведенных из одной вершины.

Р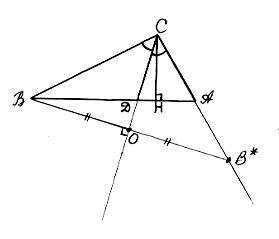ешение. Координаты точки В не удовлетворяют уравнениям высоты и биссектрисы.

Пусть высота СН: ,

биссектриса CD: 7x+y+5=0.

Найдем вершину C:

т.е. С(-1;2).

Составим уравнение стороны ВС, используя формулу (5):

;

т.е.

Из определения биссектрисы следует, что если на одной из сторон угла С дана точка В, то точка В*, симметричная точке В относительно биссектрисы CD этого угла, лежит на другой его стороне СА (см. рис.).

Таким образом, имеем:

1)

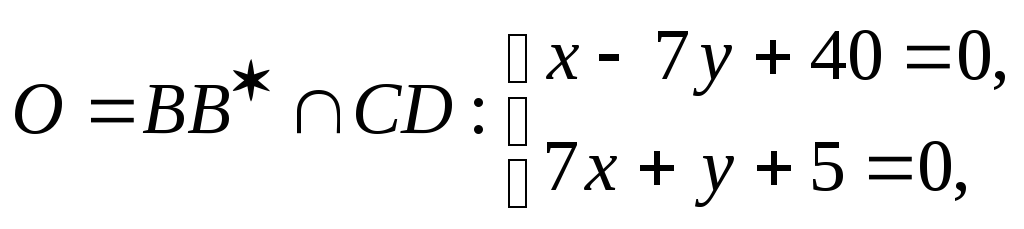
2) точка 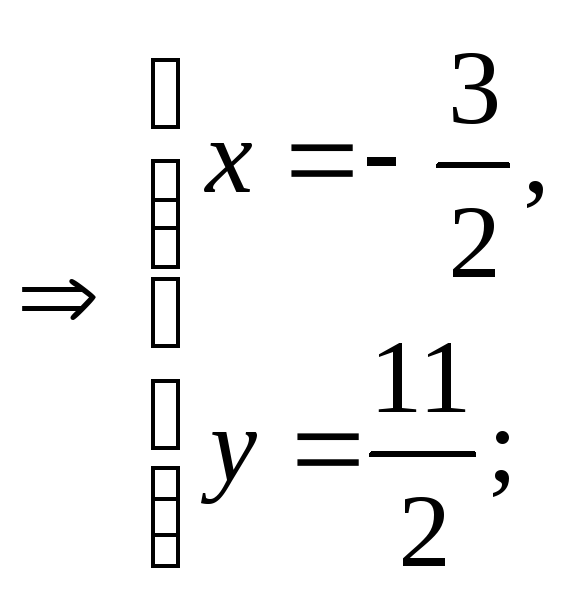т.е.

3) найдем точку В*:

т.е. В*(-5;5).

Уравнение стороны СА:

т.е. СА:

Ответ:

Задача. Составить уравнение прямой, которая проходит через точку Р(8;6) и отсекает от координатного угла треугольник с площадью, равной 12.

Решение. Запишем уравнение искомой прямой «в отрезках»:

(11)

Если найдем значения параметров a и b, задача будет решена. Т.к. точка Р лежит на искомой прямой, ее координаты удовлетворяют уравнению (11):

или

Площадь треугольника, отсекаемого прямой от координатного угла, определяется формулой: , т.к. отрезкиa и b могут быть как одного, так и разных знаков. Согласно условию задачи, имеем:

Решим систему уравнений:

Получим: Таким образом, условию задачи удовлетворяют две прямые:и

Задача. Найти уравнение биссектрисы CD треугольника АВС, заданного координатами своих вершин: А(2;-1), В(-1;3), С(2;4).

Решение. Составим уравнения сторон АС и СВ:

Биссектриса – геометрическое место точек, равноудаленных от сторон угла. Пусть М(х;у) — каждая точка биссектрисы CD, тогда или, применяя формулу (16), запишем:

Раскрывая модули, получим уравнения двух прямых:

Одна из этих прямых является биссектрисой внутреннего угла, т.е. совпадает с CD, а другая – внешнего угла треугольника АВС.

Точки А и В должны находиться по разные стороны от прямой CD, т.е. отклонения иимеют разные знаки. Оценим знаки этих отклоненийи, используя формулу (15):

,

т.е. точки А и В лежат по одну сторону от прямой . Следовательно,- биссектриса внешнего угла при вершинеС.

Ответ:

Задача. Составить уравнение прямой, проходящей через точку пересечения прямых и отсекающей на оси ординат отрезокРешить задачу, не определяя координат точки пересечения данных прямых.

Решение. Запишем уравнение пучка данных прямых:

,

т.е. - координаты нормали прямой пучка. Т.к. ,то (по условию задачи),

. Пусть , тогда.

Подставляя в уравнение пучка, найдем уравнение искомой прямой: .

Задачи для самостоятельного решения.

1. Даны две смежные вершины А(-3;-1) и В(2;2) параллелограмма ABCD и точка Q(3;0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма. (Ответ: )

2. Найти проекцию точки Р(-6;4) на прямую

(Ответ: (-2; -1))

3. Найти точку М₁, симметричную точке М₂(8;-9) относительно прямой, проходящей через точки А(3;-4) и В(-1;-2). (Ответ: М₁(10;-5))

4. Луч света направлен по прямой Дойдя до прямой луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч. (Ответ: )

5. Составить уравнения сторон треугольника, зная одну его вершину С(4;-1), а также уравнения высоты и медианы ,проведенных из одной вершины. (Ответ: )

6. Составить уравнения сторон треугольника, зная одну его вершину В(2;-7), а также уравнения высоты и медианы ,проведенных из различных вершин. (Ответ: )

7. Определить площадь треугольника, заключенного между осями координат и прямой (Ответ: 9 кв. ед.)

8. Составить уравнение прямой, которая проходит через точку Р(12;6) и отсекает от координатного угла треугольник с площадью, равной 150. (Ответ: )

9. Через точку М(3;2) провести прямую так, чтобы ее отрезок, заключенный между осями координат, делился в данной точке пополам. (Ответ: )

10. Даны уравнения двух сторон прямоугольника и одна из его вершин А(-2;1). Вычислить площадь этого прямоугольника. (Ответ: 6 кв.ед.)

11. Доказать, что прямая пересекает отрезок, ограниченный точками А(-5;1) и В(3;7)

12. Вычислить расстояние d между параллельными прямыми: 2)

(Ответ: 1) d=2,5; 2) d=0,5)

13. Точка А(5;-1) является вершиной квадрата, одна из сторон которого лежит на прямой .Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. (Ответ: 2 квадрата: 3х+4у-11=0, 4х-3у-23=0, 3х+4у-27=0; 3х+4у-11=0, 4х-3у-23=0, 3х+4у+5=0)

14. Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми: 1) x-3y+5=0, 3х-у-2=0; 2) x-2y-3=0, 2x+4y+7=0; 3) 3x+4y-1=0, 5x+12y-2=0. (Ответ: 1) 4х-4у+3=0, 2х+2у-7=0; 2) 4х+1=0, 8у+13=0; 3) 14х-8у-3=0, 64х+112у-23=0)

15. Составить уравнение биссектрисы угла между прямыми

х+2у-11=0 и 3х-6у-5=0, в котором лежит точка М(1;-3). (Ответ: 3х-19=0)

16. Составить уравнение биссектрисы острого угла, образованного двумя прямыми 3х+4х-5=0, 5х-12у+3=0. (Ответ: 7х+56у-40=0)

17. Через точку пересечения прямых 2х-5у-1=0 и х+4у-7=0 провести прямую, делящую отрезок между точками А(4;-3) и В(-1;2) в отношении (Ответ: 2х-у-5=0)

18. Найти уравнения прямых, принадлежащих пучку и перпендикулярных к каждой из основных прямых пучка. (Ответ: 14х-7у+32=0; 7х+21у-75=0)