§ 4. Векторное и смешанное произведения векторов.

Векторным произведением двух векторов и называется вектор , обозначаемый символом, илии определяемый следующими тремя условиями:

1) где, (1)

т.е. длина векторного произведения равна площади параллелограмма, построенного на векторах и;

2) т.е. векторперпендикулярен плоскости парал-лелограмма, построенного наи;

3) векторы и, взятые в указанном порядке, составляютправую тройку векторов.

Если , тов частности,; (2)

если , то

Свойства векторного произведения:

1) (3)

2) (4)

3) (5)

Если то

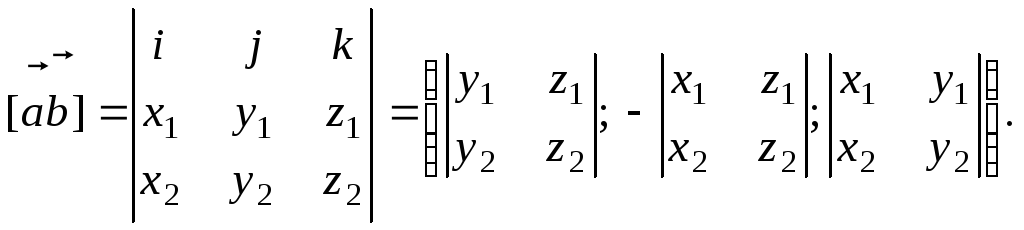(6)

Смешанным произведением трех векторов называетсячисло, равное векторному произведению умноженному скалярно на вектор, т.е.

Смешанное произведение равно объему параллелепипеда, построенного на данных трех векторах, взятому со знаком плюс, если тройка правая, и со знаком минус, если эта тройка векторов левая.

Смешанное произведение обладает тем свойством, что оно не меняется при круговой перестановке сомножителей и меняет знак при всякой перестановке, меняющей последовательность сомножителей:

(7)

Поэтому смешанное произведение векторов иобозначают проще:

, или .

Если векторы компланарны, их смешанное произведение равно нулю; т.е. равенство

(8)

есть необходимое и достаточное условие компланарности (линейной зависимости) векторов .

Если то

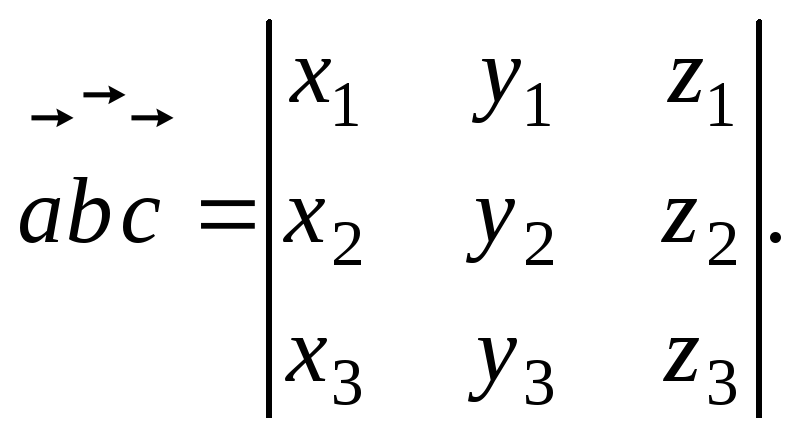(9)

Примеры решения типичных задач.

Задача. Векторы иобразуют уголЗная, чтовычислить: 1)2)3)

Решение.

1) - скалярный квадрат векторат.е. квадрат длины этого вектора:

2) вычислим сначала векторное произведение , опираясь на свойства (2)-(5):

,

т.е.

3)

Задача. Даны точки А(1;2;0), В(3;0;-3) и С(5;2;6). Вычислить площадь треугольника АВС.

Решение. Достроим до параллелограмма. Тогда пло-щадь, построенного на векторахи, равна половине площади параллелограмма, построенного на тех же векторах, т.е.

.

Найдем координаты векторов и:

Применяя формулу (6), получим:

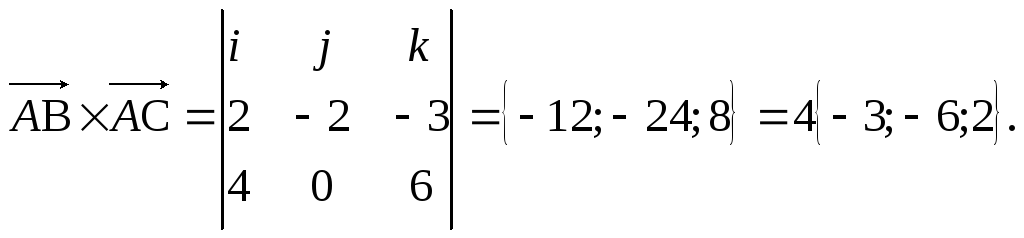
Находим длину вектора , т.е.:

кв.ед.

Таким образом, кв.ед.

Задача. Найти вектор , зная, что он перпендикулярен к векторамии удовлетворяет условию

Решение. Т.к. и, то из определения векторного произведения следует, что

.

Т.е.

Условие задачи: означает, что скалярное произведение векторана векторравно 10. Тем самым получаем уравнение относительно переменной:

Таким образом,

Задача. Вычислить объем V параллелепипеда, построенного на векторах и

Решение. Найдем смешанное произведение векторов и, опираясь на определение:

;

очевидно, что

Поэтому,

Учитывая свойство (7), получаем: Т.е.

Задача. Даны вершины тетраэдра А(2;3;1), В(4;1;-2), С(6;3;7),

D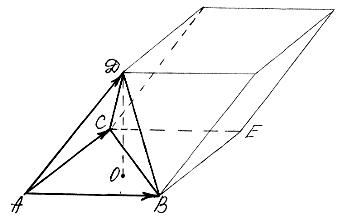(-5;-4;8). Найти длину его высоты, опущенной из вершины D.

Решение: Рассмотрим векторы и, на которых построен тетраэдрABCD. Объем тетраэдра

равен одной трети произведения площади основания на высоту:

Параллелепипед, построенный на тех же векторах, что и тетраэдр , имеет ту же высотуDO, а площадь основания (параллелограмма) – в два раза больше, т.е.

.

Для нахождения высоты тетраэдра (параллелепипеда) получим формулу:

,

или

Найдем координаты векторов и:

По формуле (9):

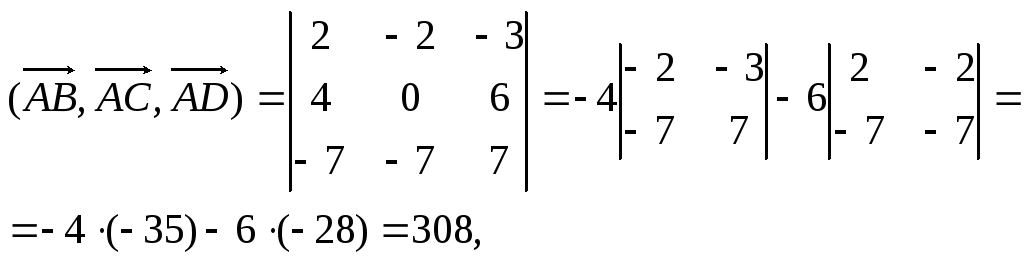
т.е. .

Вычислим

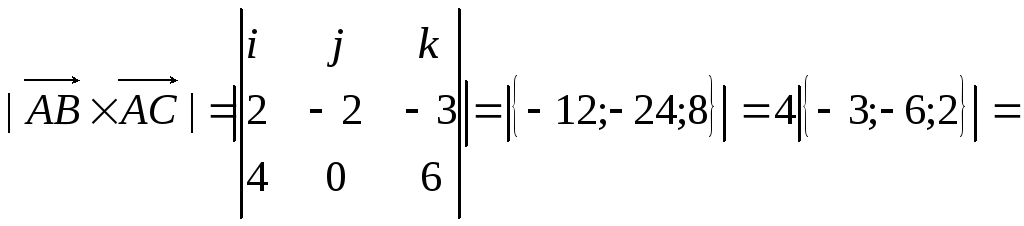
т.е.

Тогда высота DO тетраэдра ABCD будет равна

Задачи для самостоятельного решения.

1. Даны . Вычислить . (Ответ: 16)

2. Векторы ивзаимно перпендикулярны. Зная, чтовычислить: 1)2). (Ответ: 1)24; 2) 60)

3. Какому условию должны удовлетворять векторы , чтобы векторыибыли коллинеарны? (Ответ:)

4. Вычислить площадь параллелограмма, построенного на векторах и, гдеи(Ответ: 37,5 кв.ед.)

5. Разложить вектор по взаимно перпендикулярным ортам, образующим правую тройку. (Ответ:)

6. Зная векторы, совпадающие с двумя сторонами треугольника и, вычислить площадь треугольника.

(Ответ: кв.ед.)

7. Даны вершины треугольника и. Вычислить длину его высоты, опущенной из вершиныВ на сторону АС. (Ответ: 5)

8. Вычислить синус угла между диагоналями параллелограмма, построенного на данных векторах и.

(Ответ: )

9. Вектор , перпендикулярный к векторами, образует с осьюОу тупой угол. Зная, что , найти его координаты. (Ответ: )

10. Вектор , перпендикулярный к осиOz и к вектору , образует острый угол с осьюОх. Зная, что , найти его координаты. (Ответ:)

11. Векторы , образующие правую тройку, взаимно перпендикулярны. Зная, что, вычислить.

(Ответ: 24)

12. Вектор перпендикулярен к векторами, угол междуиравен 30^о. Зная, что , вычислить. (Ответ:)

13. Доказать тождество

14. Доказать, что векторы , удовлетворяющие условию, компланарны.

15. Доказать, что точки А(1;2;-1), В(0;1;5), С(-1;2;1), D(2;1;3) лежат в одной плоскости.

16. Вычислить объем параллелепипеда, построенного на трех данных векторах и, и исследовать, образуют ли векторы левую или правую тройку. (Ответ:куб.ед., левая тройка)

17. Объем тетраэдра , три его вершины находятся в точкахА(2;1;-1), В(3;0;1), С(2;-1;3). Найти координаты четвёртой вершины D, если известно, что она лежит на оси Оу. (Ответ: )

18. Найти вектор , одновременно удовлетворяющий трем уравнениям:. (Ответ:)