
АиГ / тема 10
.docКурс “Алгебра и Геометрия”
(спец. прикладная математика, информатика, 1 курс, 1 семестр)
Тема 10. Прямая и плоскость в пространстве. − 4 ч.
Содержание: смешанные задачи, относящиеся к уравнению плоскости и уравнениям прямой. Взаимное расположение прямой и плоскости в пространстве. Кратчайшее расстояние между двумя прямыми в пространстве.
Цель: сформировать навыки применения метода координат для решения стереометрических задач о плоскостях и прямых в пространстве.
Форма контроля: опрос.
Задачи
Задача 1 ([8], 1038).
Доказать, что прямая
![]() ,
,
![]() ,
,
![]() параллельна плоскости
параллельна плоскости
![]() .
.
Задача 2 ([8], 1039).
Доказать, что прямая
![]() ,
,
![]() лежит в плоскости
лежит в плоскости
![]() .
.
Задача 3 ([8], 1040). Найти точку пересечения прямой и плоскости:
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() .
.
Задача 4 ([8], 1041).
Составить канонические уравнения
прямой, проходящей через точку
![]() и середину отрезка прямой
и середину отрезка прямой
![]() ,
,
![]() ,
заключенного между плоскостями
,
заключенного между плоскостями
![]() ,
,
![]() .
.
Задача 5 ([8], 1042).
Составить уравнения прямой, проходящей
через точку
![]() перпендикулярно к плоскости
перпендикулярно к плоскости
![]() .
.
Задача 6 ([8], 1043).
Составить уравнение плоскости, проходящей
через точку
![]() перпендикулярно к прямой
перпендикулярно к прямой
![]() .
.
Задача 7 ([8], 1044).
Составить уравнение плоскости, проходящей
через точку
![]() перпендикулярно к прямой
перпендикулярно к прямой
![]() ,
,
![]() .
.
Задача 8 ([8], 1045).
При каком значении
![]() прямая
прямая
![]() параллельна плоскости
параллельна плоскости
![]() ?
?
Задача 9 ([8], 1046).
При каком значении
![]() прямая
прямая
![]() ,
,
![]() параллельна плоскости
параллельна плоскости
![]() ?
?
Задача 10 ([8],
1047).
При каких значениях
![]() и
и
![]() прямая
прямая
![]() ,
,
![]() ,
,
![]() лежит в плоскости
лежит в плоскости
![]() ?
?
Задача 11 ([8],
1048). При каких
значениях
![]() и
и
![]() плоскость
плоскость
![]() перпендикулярна к прямой
перпендикулярна к прямой
![]() ,
,
![]() ,
,
![]() ?
?
Задача 12 ([8],
1049). При каких
значениях
![]() и
и
![]() прямая
прямая
![]() перпендикулярна к плоскости
перпендикулярна к плоскости
![]() ?
?
Задача 13 ([8],
1050). Найти
проекцию точки
![]() на прямую
на прямую
![]() ,
,
![]() ,
,
![]() .
.
Задача 14 ([8],
1051). Найти
точку
![]() ,
симметричную точке
,
симметричную точке
![]() относительно прямой
относительно прямой
![]() ,
,
![]() .
.
Задача 15 ([8],
1052). Найти
точку
![]() симметричную точке
симметричную точке
![]() относительно прямой, проходящей через
точки
относительно прямой, проходящей через
точки
![]() и
и
![]() .
.
Задача 16 ([8],
1053). Найти
проекцию точки
![]() на плоскость
на плоскость
![]() .
.
Задача 17 ([8],
1054). Найти
точку
![]() ,
симметричную точке
,
симметричную точке
![]() относительно плоскости
относительно плоскости
![]() .
.
Задача 18 ([8],
1055). На
плоскости Oxy
найти точку
![]() ,
сумма расстояний которой до точек
,
сумма расстояний которой до точек
![]() и
и
![]() была бы наименьшей.
была бы наименьшей.
Задача 19 ([8],
1056). На
плоскости Oxz
найти такую точку
![]() ,
разность расстояний которой до точек
,
разность расстояний которой до точек
![]() и
и
![]() была бы наибольшей.
была бы наибольшей.
Задача 20 ([8],
1057). На
плоскости
![]() найти такую точку
найти такую точку
![]() ,
сумма расстояний которой до точек
,
сумма расстояний которой до точек
![]() и
и
![]() была бы наименьшей.
была бы наименьшей.
Задача 21 ([8],
1058). На
плоскости
![]() найти такую точку
найти такую точку
![]() ,
разность расстояний которой до точек
,
разность расстояний которой до точек
![]() и
и
![]() была бы наибольшей.
была бы наибольшей.
Задача 22 ([8],
1059). Точка
![]() движется прямолинейно и равномерно из
начального положения
движется прямолинейно и равномерно из
начального положения
![]() со скоростью
со скоростью
![]() в направлении вектора
в направлении вектора
![]() .
Убедившись, что траектория точки
.
Убедившись, что траектория точки
![]() пересекает плоскость
пересекает плоскость
![]() ,
найти:
,
найти:
-
точку
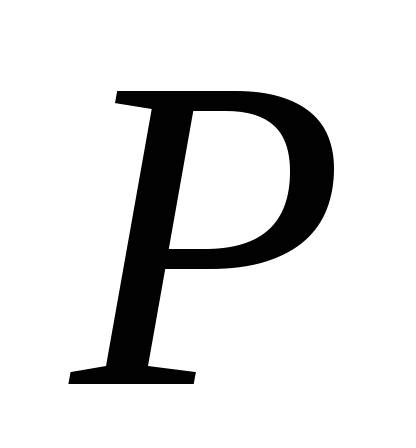 их пересечения;
их пересечения; -
время, затраченное на движение точки
 от
от
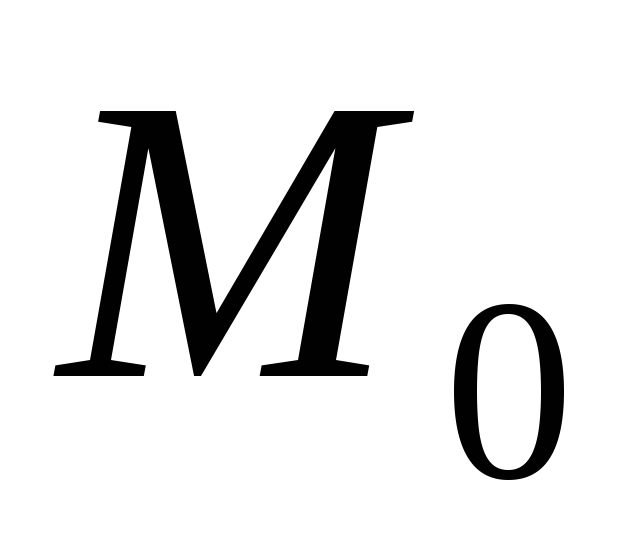 до
до
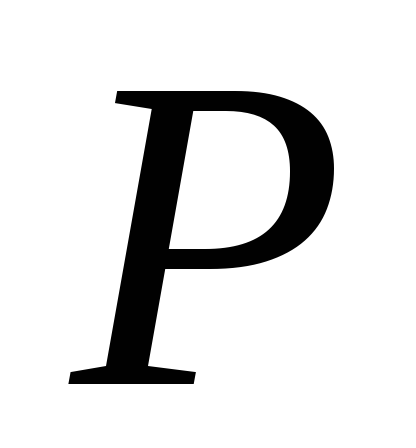 ;
; -
длину отрезка
 .
.
Задача 23 ([8],
1060). Точка
![]() движется прямолинейно и равномерно из
начального положения
движется прямолинейно и равномерно из
начального положения
![]() со скоростью
со скоростью
![]() по перпендикуляру, опущенному из точки
по перпендикуляру, опущенному из точки
![]() на плоскость
на плоскость
![]() .
Составить уравнение движения точки
.
Составить уравнение движения точки
![]() и определить:
и определить:
-
точку
 пересечения её траектории с этой
плоскостью;
пересечения её траектории с этой
плоскостью; -
время, потраченное на движение точки
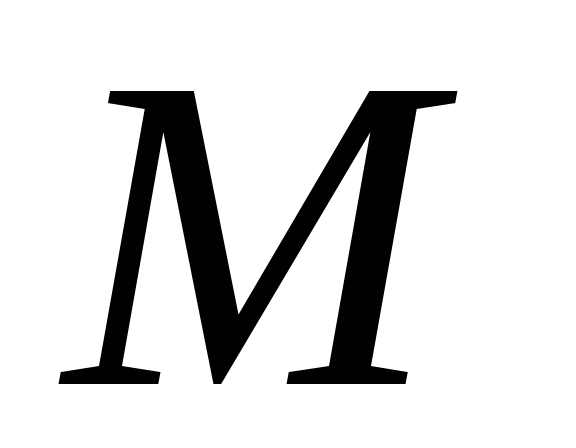 от
от
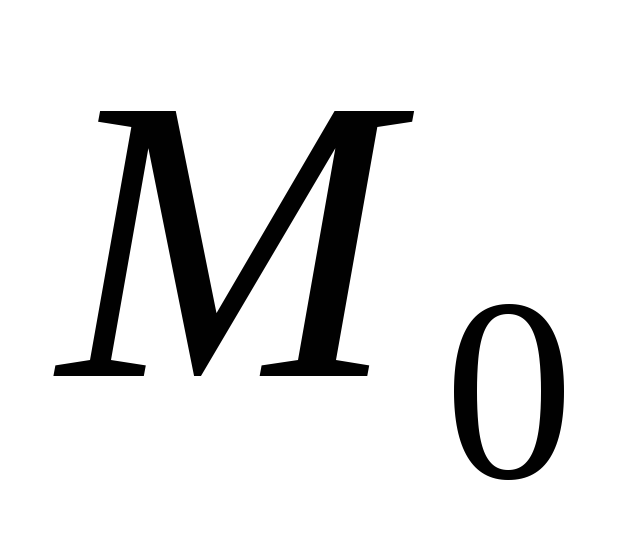 до
до
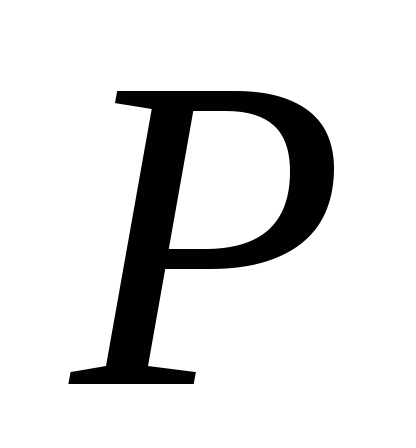 ;
; -
длину отрезка
 .
.
Задача 24 ([8],
1061). Точка
![]() движется прямолинейно и равномерно из
начального положения
движется прямолинейно и равномерно из
начального положения
![]() в направлении вектора
в направлении вектора
![]() со скоростью
со скоростью
![]() .
Определить, за какое время она пройдет
отрезок своей траектории, заключенный
между параллельными плоскостями
.
Определить, за какое время она пройдет
отрезок своей траектории, заключенный
между параллельными плоскостями
![]() .
.
Задача 25 ([8],
1062). Вычислить
расстояние
![]() точки
точки
![]() от прямой
от прямой![]()
Задача 26 ([8],
1063). Вычислить
расстояние
![]() от точки
от точки
![]() до следующих прямых:
до следующих прямых:
1)
![]()
2)
![]() ,
,
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() .
.
Задача 27 ([8], 1064). Убедившись, что прямые
![]() ,
,
![]() ,
,
![]()
параллельны,
вычислить расстояние
![]() между ними.
между ними.![]()
Задача 28 ([8],
1065). Составить
уравнение плоскости, проходящей через
![]() параллельно прямым
параллельно прямым
![]() ,
,
![]()
Задача 29 ([8],
1068). Составить
уравнение плоскости, проходящей через
прямую
![]() ,
,
![]() ,
,
![]() и точку
и точку
![]() .
.
Задача 30 ([8],
1070). Доказать,
что прямые
![]()
![]() ,
,
![]() ,
,
![]() лежат в одной плоскости, и составить
уравнение этой плоскости.
лежат в одной плоскости, и составить
уравнение этой плоскости.
Задача 31 ([8],
1072). Составить
уравнение плоскости, проходящей через
две параллельные прямые
![]() ,
,
![]() .
.
Задача 32 ([8],
1074). Найти
проекцию точки
![]() на плоскость, проходящую через параллельные
прямые
на плоскость, проходящую через параллельные
прямые
![]() ,
,
![]() .
.
Задача 33 ([8],
1075). Найти
точку
![]() ,
симметричную точке
,
симметричную точке
![]() относительно плоскости, проходящей
через
относительно плоскости, проходящей
через
![]() ,
,
![]() и
и
![]() .
.
Задача 34 ([8],
1076). Найти
точку
![]() ,
симметричную точке
,
симметричную точке
![]() относительно плоскости, проходящей
через прямые
относительно плоскости, проходящей
через прямые
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Задача 35 ([8],
1077). Составить
уравнение плоскости, проходящей через
прямую
![]() ,
,
![]() ,
,
![]() параллельно прямой
параллельно прямой
![]() ,
,
![]() .
.
Задача 36 ([8],
1079). Составить
уравнение плоскости, проходящей через
прямую
![]() перпендикулярно к плоскости
перпендикулярно к плоскости
![]() .
.
Задача 37 ([8],
1081). Составить
канонические уравнения прямой, которая
проходит через точку
![]() параллельно плоскости
параллельно плоскости
![]() и пересекает прямую
и пересекает прямую
![]()
Задача 38 ([8], 1082). Составить параметрические уравнения прямой, которая параллельна плоскостям
3х +12y – 3z – 5 = 0, 3x – 4y + 9z + 7 = 0
и пересекает прямые
![]() ,
,
![]() .
.
Задача 39 ([8], 1083). Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев:
-
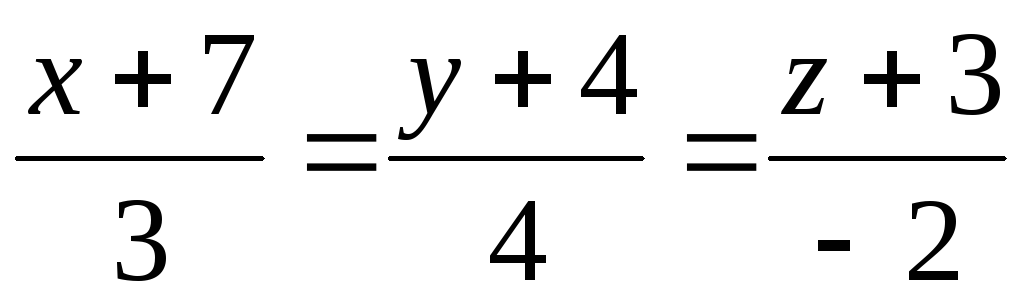 ,
,
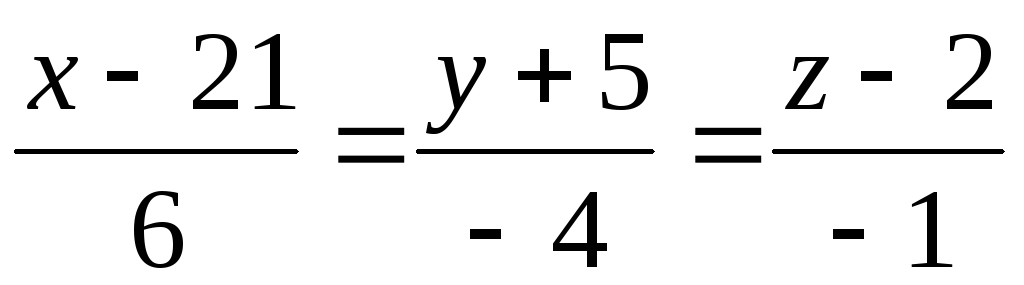 ;
; -
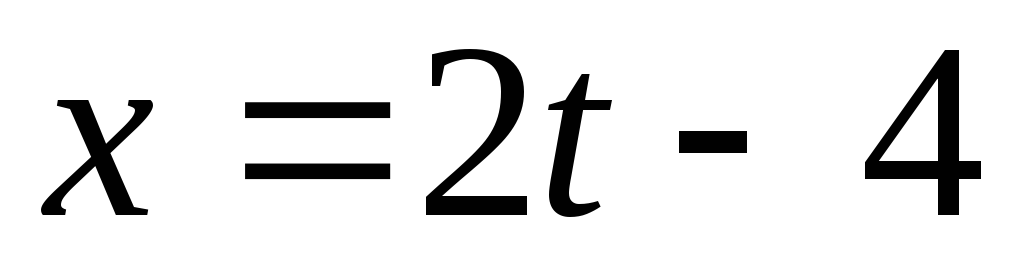 ,
,
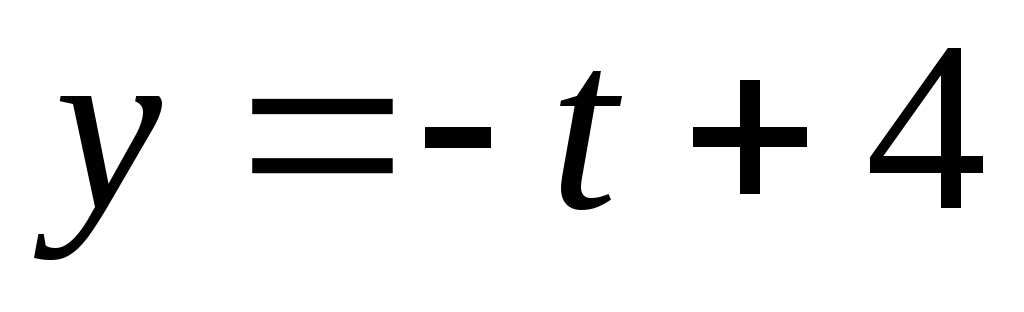 ,
,
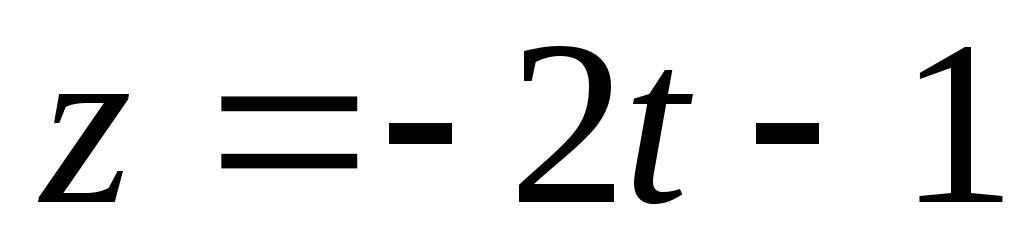 ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
Тема 10.
Ответы
Задача 3 ([8],
1040). 1)
![]() ;
2)
Прямая,
парлелльна плоскости;
3)
Прямая лежит на плоскости.
;
2)
Прямая,
парлелльна плоскости;
3)
Прямая лежит на плоскости.
Задача 6 ([8], 1043).
![]() .
.
Задача 7 ([8], 1044).
![]() .
.
Задача 8 ([8], 1045).
![]() .
.
Задача 9 ([8], 1046).
![]() .
.
Задача 10 ([8],
1047).
![]() ,
,
![]() .
.
Задача 11 ([8],
1048).
![]() ,
,
![]() .
.
Задача 12 ([8],
1049).
![]() ,
,
![]() .
.
Задача 13 ([8],
1050).
![]() .
.
Задача 14 ([8],
1051).
![]() .
.
Задача 15 ([8],
1052).
![]() .
.
Задача 16 ([8],
1053).
![]() .
.
Задача 17 ([8],
1054).
![]() .
.
Задача 18 ([8],
1055).
![]() .
.
Задача 20 ([8],
1057).
![]() .
.
Задача 21 ([8],
1058).
![]() .
.
Задача 22 ([8],
1059). 1)
![]() .
.
Задача 23 ([8],
1060).
![]() ,
,
![]() ,
,
![]() ;
;
1)
![]() ;
2)
От
;
2)
От
![]() до
до
![]() ;
3)
;
3)
![]() .
.
Задача 24 ([8], 1061). За промежуток времени, равный 3.
Задача 25 ([8],
1062).
![]() .
.
Задача 26 ([8], 1063). 1) 21; 2) 6; 3) 15.
Задача 27 ([8],
1064).
![]() .
.
Задача 28 ([8],
1065).
![]() .
.
Задача 29 ([8],
1068).
![]() .
.
Задача 30 ([8],
1070).
![]() .
.
Задача 32 ([8],
1074).
![]() .
.
Задача 33 ([8],
1075).
![]() .
.
Задача 34 ([8],
1076).
![]() .
.
Задача 35 ([8],
1077).
![]() .
.
Задача 36 ([8],
1079).
![]() .
.
Задача 38 ([8],
1082).
![]() ,
,
![]() ,
,
![]() .
.
Задача 39 ([8],
1083). 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
