2. Отношения. Отображения множеств

Содержание: Отношения. Отношения эквивалентности и порядка. Отображения.

Следует научиться доказывать свойства отношений, находить образы и прообразы множеств для заданных отображений и проверять соотношения, связывающие образы и прообразы множеств.

Некоторые определения и обозначения

Бинарное отношение − это множество, элементами которого являются упорядоченные пары.

Пусть R − бинарное отношение.

aRb означает, что ; в этом случае говорят, что параудовлетворяет отношениюR, или что элемент a находится в отношении R к элементу b.

Область определения R − это множество .

Область значений R − это множество .

Обратное отношение к отношению R, обозначаемое через , определяется следующим образом:.

Композицией (или произведением) отношений R и S называется отношение

.

Для любого множества M полагаем

, .

называют R-образом, а −R-прообразом множества M. При этом −-образ множестваM.

Если , то(иногда – и само R ) называют отношением между элементами множества A и элементами множества B; при этом если A = B, то R – отношение на множестве A.

Отношение R называется

транзитивным, если для любых a, b, c из aRb и bRc следует, что aRc;

симметричным, если для любых a, b из aRb следует bRa;

антисимметричным, если для любых a, b из aRb и bRa следует, что a = b.

Отношение R на множестве A называется

рефлексивным, если aRa для каждого ;

эквивалентностью, если это отношение рефлексивно, симметрично и транзитивно;

порядком, если это отношение транзитивно и антисимметрично; при этом рефлексивный порядок часто называют нестрогим порядком.

Если R − отношение эквивалентности на множестве A, то обозначает фактор-множествомножестваA по отношению эквивалентности R; для каждого множествоназывается классом эквивалентности элементаa по отношению эквивалентности R.

Множество называется упорядоченным, если на нем задан некоторый порядок.

Если R – порядок на множестве A, , то– порядок наB (говорят, что подмножество упорядоченного множества является упорядоченным множеством).

Множество A с порядком R называется линейно упорядоченным, если для любой пары a, b его элементов либо aRb, либо bRa.

Бинарное отношение R называется функциональным, или отображением (иногда – функцией), если для любого a, принадлежащего области определения R, − одноэлементное множество.

Пусть R − отображение, a принадлежит области определения R и . Тогдаобозначает элементb, называемый образом элемента a при отображении R; называетсяпрообразом элемента b при отображении R.

Композиция (произведение) отображений − отображение. Отношение, обратное к отображению R, будет отображением тогда и только тогда, когда R инъективно, т.е. когда для каждого b множество содержит не более одного элемента.

Если A – область определения отображения R, то для используют обозначениеи говорят, чтоR является отображением множества A и отображает A в B. Для такого отображения используется также обозначение

(или ).

Отображение называется отображениемA на B, или сюръективным отображением, если . Биекция – это отображение, одновременно и сюръективное, и инъективное.

обозначает множество всех отображений A в B.

Индексированное множество − это отображениеx, определенное на множестве S (называемом множеством индексов) и сопоставляющее каждому индексу соответствующий элемент;– другое обозначение для.− это множествовсех значений отображенияx.

Если n − целое положительное число и , тобудем отождествлять с упорядоченнойn-кой .

Последовательность − это индексированное множество, множество индексов которого − множество всех натуральных чисел.

Подпоследовательность последовательности x − это композиция последовательностиx и последовательности , для которой, что означает следующее:

.

Любое множество A можно естественным образом рассматривать как индексированное, считая каждый элемент множества A индексом этого же элемента.

Функцией выбора множества называется отображениеf множества S, удовлетворяющее следующему условию:

.

Аксиома выбора утверждает, что для каждого индексированного семейства непустых множеств существует функция выбора этого семейства.

Если , тоиобозначают множество всех функций выбора индексированного семействаX; это множество называется декартовым произведением семейства X. Для прииспользуются обозначения

, ,

а при используется обозначение.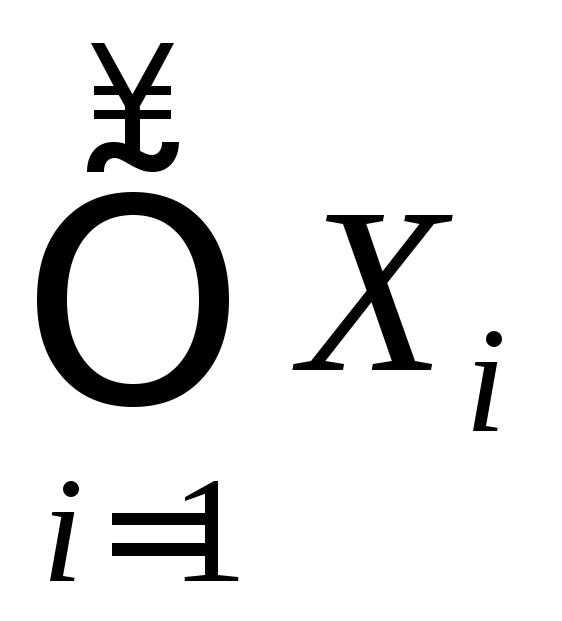

Пусть A X . Характеристическая функция множестваA (точнее, подмножества A множества X ) определяется равенством