Лабораторная работа № 12

Лабораторная работа № 12 исследование затухающих колебаний

Ц ель работы. Изучение затухающих колебаний в колебательном контуре при различных величинах параметров L, С, R, расчет логарифмического декремента затухания.

Приборы и оборудование. Установка для изучения законов переменного тока в составе: магазин индуктивностей, магазин емкостей, магазин сопротивлений, коммутатор, источник питания, осциллограф С1-65.

1.Электромагнитные колебания

1.1. Колебательный контур

Рассмотрим процессы, протекающие в электрической цепи, состоящей из последовательно соединенных конденсатора С, катушки индуктивности L и омического сопротивления R (рис. 12.1). Такая цепь называется колебательным контуром¹.

Внешняя электродвижущая сила создает в цепи переменное напряжение, изменяющееся по косинусоидальному закону:

. (12.1)

Ток, текущий в колебательном контуре, считается квазистационарным, т. е. таким, когда во всех элементах последовательной электрической цепи его значение в данный момент одинаково². Мгновенное значение напряжения на конденсаторе такое же, как и при тех же, но неизменных во времени зарядах на его пластинах. Для мгновенных значений квазистационарных токов справедливы законы, установленные для цепей постоянного тока. Пусть Q — заряд конденсатора в данный момент времени, U — разность потенциалов на его пластинах. Тогда

, (12.2)

так как положительному направлению тока (рис. 12.1) соответствует убывание заряда конденсатора. По закону Ома имеем

, (12.3)

где — электродвижущая сила самоиндукции в катушке:

. (12.4)

Подставляя (12.1), (12.2) и (12.4) в (12.3)·, имеем

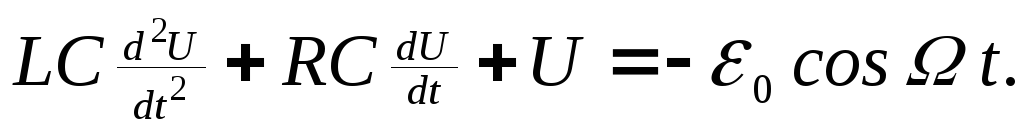(12.5)

Разделим уравнение (12.5) на LC и введем обозначения

Тогда после преобразований получим дифференциальное уравнение (12.6), являющееся уравнением колебательного контура:

. (12.6)

1.2. Гармонические колебания

При отсутствии в контуре омического сопротивления (R = 0) и внешней электродвижущей силы процесс разряда конденсатора через катушку индуктивностью L описывается уравнением³ (12.7), в которое переходит (12.6) при ₀ = 0 и  = 0:

. (12.7)

Для его решения умножим уравнение (12.7) на U и в результате преобразований придем к уравнению (12.8) :

. (12.8)

Из (12.8) следует, что при разряде конденсатора в колебательном контуре величина U²+₀²U² остается неизменной. Пусть в начальный момент времени сила тока в контуре I =CU =0, напряжение на конденсаторе равно U₀. Тогда равенство (12.8) может быть записано в виде

, (12.9)

или

_, (12.10)

где LI²/₂— энергия магнитного поля катушки, CU²/₂ — энергия электрического поля конденсатора. Уравнение (12.10) представляет собой закон сохранения энергии в колебательном контуре. После разделения переменных

(12.11)

уравнение (12.9) может быть проинтегрировано.

В результате получим

,

или

- уравнение гармонических колебаний⁴. Постоянные U₀ и  определяются из начальных условий, -циклическая частота колебаний. Промежуток времени, через который напряжение периодически повторяется, называется периодом колебаний Т.

Из уравнения (12.12) следует, что. T₀ = 2. Тогда

(12.13)

- формула Томсона^{5 6}.

1.3. Затухающие колебания

Реальный контур обладает сопротивлением R. Энергия, запасенная в контуре, постепенно расходуется на джоулево тепло, поэтому свободные колебания затухают⁷. Дифференциальное уравнение свободных колебаний в колебательном контуре получается из (12.6) при отсутствии внешней электродвижущей силы:

_. (12.14)

Для его решения введем новую переменную x(t):

. (12.15)

В результате подстановки (12.15) в (12.14) получим уравнение (12.16), которое совпадает с дифференциальным уравнением гармонических колебаний при ² - ² > 0:

. (12.16)

Его решение [см. (12.12)] имеет вид

, (12.17)

где ; U₀ и  — постоянные, определяемые начальными условиями.

Зависимость напряжения на конденсаторе колебательного контура от времени получается подстановкой (12.17) в (12.15):

. (12.18)

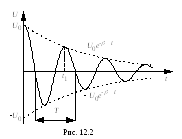
График зависимости U(t) изображен на рис. 12.2. Из рисунка видно, что кривая U(t) периодически проходит через нуль и максимальные значения. Описываемый уравнением (12.18) процесс называется затухающими колебаниями⁸. Промежуток времени Т называется периодом затухающих колебаний:

(12.19)

а величина

(12.20)

называется амплитудой затухающих колебаний. За время амплитуда колебаний уменьшается в е раз. Степень затухания принято характеризовать логарифмическим декрементом затухания , равным натуральному логарифму от отношения двух последовательных максимумов или минимумов:

. (12.21)

Он связан с числом полных колебаний N, совершаемых за время,зависимостью

. (12.22)

Величина называется добротностью колебательного контура. При малом затухании добротность Q можно вычислить по формуле (5.23)⁹:

. (12.23)

Добротность Q связана с относительной убылью энергии контура за один период колебаний зависимостью

(12.24)

Здесь W — энергия, запасенная в контуре, W — уменьшение энергии за один период. Действительно,

, (12.25)

так как энергия контура пропорциональна квадрату амплитуд напряжение на конденсаторе:

.

При условии, что (малое затухание), , поэтому

,

откуда .

При период T затухающих колебаний устремляется в бесконечность.

В этом предельном случае уравнение (12.16) переходит в уравнение

(12.25)

имеет решение

,

где а и b — постоянные интегрирования.

Уравнение U(t), описывающее процесс изменения напряжения на конденсаторе, в этом случае имеет вид

.

Процесс изменения напряжения на конденсаторе будет апериодическим. Графики U(t) при разных значениях а и b приведены на рис. 12.3. Сопротивление R_кр, при котором колебательный процесс в контуре переходит в апериодический, называется критическим. Критическое сопротивление¹⁰ R_кр определяется из условия , откуда (12.26)

При R > R_кр апериодический характер процессов в колебательном контуре сохраняется.

2. Установка для наблюдения затухающих колебаний

Наиболее простой способ возбуждения собственных колебаний в колебательном контуре реализован в установке принципиальная схема, которой приведена на рис. 12.4.

Коммутатор К представляет собой переключатель, который с частотой 50 Гц подключает конденсатор попеременно то к источнику питания то к индуктивности. На выходе коммутатора формируется импульсы напряжения в форме меандра длительность t_ком = 0.02. В течение времени t_ком конденсатор подключен к источнику и заряжается до напряжения питания. Потом в течение следующих t_иком = 0.02 с конденсатор разряжается через контур и в колебательном контуре возникают затухающие колебания (рис. 12.5).

В колебательном контуре происходит непрерывный процесс преобразования электрической энергии конденсатора в магнитную энергию катушки и на оборот. В первый момент времени, как только коммутатор замкнет цепь колебательного контура, конденсатор начнет разряжаться и по цепи потечет ток.

Р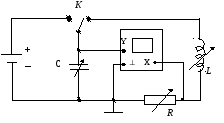 ис. 12.4. Принципиальная схема установки

Ток, текущий по виткам катушки вызовет появление магнитного поля и ЭДС самоиндукции в катушке. В начале самоиндукция будет препятствовать нарастанию тока. Так будет продолжаться до того момента пока конденсатор полностью не разрядиться, а магнитное поле в катушке не достигнет максимума. Теперь ЭДС самоиндукции поменяет направление, стремясь подержать ток на неизменном уровне. По мере уменьшения магнитного поля движение зарядов в контуре будет продолжаться, но ток будет течь уже в обратном направлении. Этот ток приведет к зарядке конденсатора с противоположной полярностью. В момент, когда магнитное поле катушки станет равным нулю, напряжение на конденсаторе достигнет максимума и все процессы повторятся вновь. Напряжение с конденсатора поступает на вход Y осциллографа. При включенной развертке на экране можно наблюдать кривую затухающих колебаний (рис. 12.5).

Когда R > R_кр колебательный процесс переходит в апериодический. Основные причины затухания колебаний в реальном контуре следующие: наличие омического сопротивления проводников, потери на излучение, потери в конденсаторе¹¹.

В ряде случаев колебательный процесс удобно изучать в системе координат I – U , где U – напряжение на конденсаторе, а I – ток в контуре. Плоскость I – U называют фазовой плоскостью, а кривую изображающая зависимость силы тока от напряжения – фазовой кривой. Для наблюдения на экране осциллографа сигнала пропорционального току, текущему в контуре на вход (← X) подается напряжение снимаемое с сопротивления R. Осциллограф включается в режим наблюдения фигур Лиссажу. Рассмотрим вид фазовой кривой для случая R=0. Уравнение гармонических колебаний в этом случае

U = U₀ cos(₀t + ). (12.27)

Сила тока в контуре равна

I = − C•^dU/_dt = CU₀₀sin(₀t+) (12.28)

Исключив из уравнений (12.27) и (12.28) время, получим уравнение фазовой кривой:

Э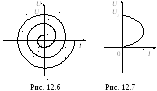то уравнение эллипса. В случае затухающих колебаний напряжение и сила тока в контуре непрерывно убывают, а фазовая кривая превращается спираль, непрерывно приближающуюся к фокусу О (рис. 12.6). При R > R_кр колебательный процесс в контуре прекращается, и спираль переходит в кривую, изображенную на рис. 12.7.