
Пример автоколебаиия
Рассмотрим уравнение:
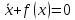 ,
(*)
,
(*)
в
котором функция
 удовлетворяет условиям:
удовлетворяет условиям:
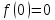 и
и
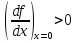 .
.
Уравнение
(*) описывает движения некоторой
консервативной системы с одной степенью
свободы. В малой окрестности положения
равновесия
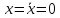 уравнение (*) определяет колебательые
движения, которые происходят с постоянной
амплитудой. Фазовая плоскость этого
уравнения в окрестности этой точки
целиком заполнена замкнутыми кривыми.
Будем называть некоторую силу
уравнение (*) определяет колебательые
движения, которые происходят с постоянной
амплитудой. Фазовая плоскость этого
уравнения в окрестности этой точки
целиком заполнена замкнутыми кривыми.
Будем называть некоторую силу
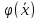 ,
зависящую только от скорости, диссипативной,
если для любого
,
зависящую только от скорости, диссипативной,
если для любого
 она удовлетворяет условию:
она удовлетворяет условию:
 .
(**)
.
(**)
Преположим
теперь, что колебания маятника приходят
под действием консервативний силы
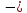
 и диссипативной силы
и диссипативной силы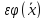 ,
где
,
где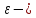 некоторый малый параметр:
некоторый малый параметр:
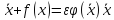 .
(***)
.
(***)
Если
теперь умножить (***) на
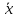 ,
то оно примет вид:
,
то оно примет вид:
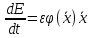 ,
,
где
 полная энергия маятника:
полная энергия маятника:
 .
.
Так как имеет место неравенство (**), то в любой момент времени:
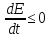 ,
,
причем
равенство имеет место только для тех
значений
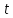 ,
для которых
,
для которых
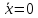 .
Таким образом, колебания происходящие
под действием консервативной и
диссипативной силы затухают. Рассмотрим
фазовую плоскость уравнения (***).
.
Таким образом, колебания происходящие
под действием консервативной и
диссипативной силы затухают. Рассмотрим
фазовую плоскость уравнения (***).
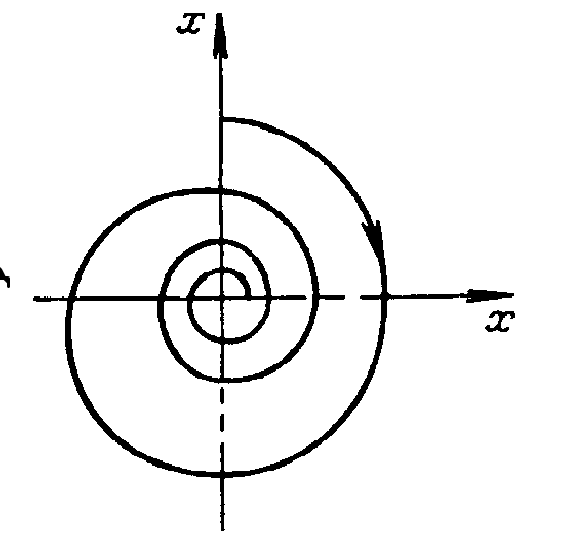
(рис.1)
Пусть
в некоторый момент времени
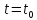 система находится в состоянии
система находится в состоянии Начальное значение энергии будет
Начальное значение энергии будет .
По прошествии некоторого времени
изображающая точка, двигаясь вдоль
фазовой траектории, совершит полный
оборот вокруг начала координат и снова
пересечет ось ординат в некоторой точке
.
По прошествии некоторого времени
изображающая точка, двигаясь вдоль
фазовой траектории, совершит полный
оборот вокруг начала координат и снова
пересечет ось ординат в некоторой точке ,
причем
,
причем .
Следовательно,
.
Следовательно,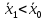 .
Заметим еще, что две фазовые траектории
не могут пересекаться
.
Заметим еще, что две фазовые траектории
не могут пересекаться через каждую точку фазовой плоскости,
которая не является особой, проходит
только одна фазовая траектория.
Система (***) имеет только одну особую
точку
через каждую точку фазовой плоскости,
которая не является особой, проходит
только одна фазовая траектория.
Система (***) имеет только одну особую
точку начало координат. Таким образом, фазовый
портрет уравнения (***) имеет вид,
изображенный на рис.1. Начало координат
является особой точкой типа фокус.
Изображающая точка движется в направлении,
указанном стрелкой . Фазовые траектории
наматываются на фокус. Следовательно,
в рассматриваемом случае фокус будет
устойчивой особой точкой.
начало координат. Таким образом, фазовый
портрет уравнения (***) имеет вид,
изображенный на рис.1. Начало координат
является особой точкой типа фокус.
Изображающая точка движется в направлении,
указанном стрелкой . Фазовые траектории
наматываются на фокус. Следовательно,
в рассматриваемом случае фокус будет
устойчивой особой точкой.
Алгоритм построения автоколебательных режимов в случае квазилинейных систем
На основе учебника Н.Н. Моисеева [1] (стр. 79-96) начнем изучение эффективных методов построения автоколебательных режимов с иследования квазилинейных уравнения вида:
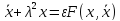 .
(1)
.
(1)
Следует
ожидать, что период автоколебательного
режима зависит от параметра
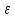 :
:
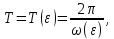
причем
 условимся называть частотой. Будем
искать режимы, частота которых обладает
следующим свойством:
условимся называть частотой. Будем
искать режимы, частота которых обладает
следующим свойством:
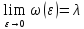 .
.
На этом основании положим:
 (2)
(2)
и сделаем замену независимого переменного:
 .
(3)
.
(3)
Значению
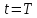 отвечает значение
отвечает значение
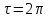 т.е период искомого решения относительно
новой переменной теперь снова фиксированной
т.е период искомого решения относительно
новой переменной теперь снова фиксированной он равен
он равен .
Числа
.
Числа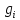 должны быть определены в процессе
построения решения. Перепишем уравнение
(1), сделав в нем замену (2):
должны быть определены в процессе
построения решения. Перепишем уравнение
(1), сделав в нем замену (2):
 .
(4)
.
(4)
Поскольку
уравнение (1) и (4) не содержат времени и
уравнение (4) инвариантно относительно
преобразования
 ,
нам достаточно рассмотреть следующую
задачу Коши:
,
нам достаточно рассмотреть следующую
задачу Коши:
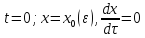 .
(5)
.
(5)
Заметим,
что величина
 также заранее неизвестна. Итак, мы пришли
к задаче отыскания числа
также заранее неизвестна. Итак, мы пришли
к задаче отыскания числа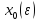 и периодического решения уравнения (4)
периода
и периодического решения уравнения (4)
периода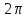 ,
которое определяется этим числом.
Решение такой задачи будем искать в
виде ряда, расположенного по степеням
параметра
,
которое определяется этим числом.
Решение такой задачи будем искать в
виде ряда, расположенного по степеням
параметра :
:
 .
(6)
.
(6)
Функции
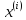 удовлетворяют следующим уравнениям:
удовлетворяют следующим уравнениям:
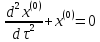 ,
(7)
,
(7)
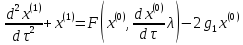 .
(8)
.
(8)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Выпишем общее решение уравнения (7):
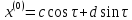 ,
,
но
в силу (5)
 ,
т.е.
,
т.е.
 .
(9)
.
(9)
Величина
 апмлитуда порождающего решения нам
неизвестна. На этом шаге алгоритма она
остается неопределенной. Рассмотрим
теперь уравнение (8). Его можно переписать
в виде:
апмлитуда порождающего решения нам
неизвестна. На этом шаге алгоритма она
остается неопределенной. Рассмотрим
теперь уравнение (8). Его можно переписать
в виде:
 ,
(10)
,
(10)
где
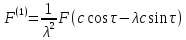
и
является некоторой периодической
функцией
 периода
периода .
Для того, чтобы уравнение (10) допускало
периодические решения, необходима и
достаточна ортогональность правой
части этого уравнения функциями
.
Для того, чтобы уравнение (10) допускало
периодические решения, необходима и
достаточна ортогональность правой
части этого уравнения функциями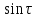 и
и :
:
 ,
(11)
,
(11)
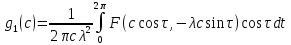 .
(12)
.
(12)
Первое
из этих уравнений представляет собой
некоторое трансцендентное1уравнения для определения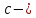 амплитуды порождающего решения. Уравнение
может вообще не иметь решения. Это будет
в том случае, когда система (1) не допускает
автоколебательных режимов, например в
том случае когда сила
амплитуды порождающего решения. Уравнение
может вообще не иметь решения. Это будет
в том случае, когда система (1) не допускает
автоколебательных режимов, например в
том случае когда сила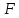 является диссипативной2.
Уравнение (11) может вообще не иметь
конечное число решений. Уравнение (11)
может оказаться тождеством, справедливым
для любого значения
является диссипативной2.
Уравнение (11) может вообще не иметь
конечное число решений. Уравнение (11)
может оказаться тождеством, справедливым
для любого значения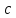 .
Такая ситуация имеет место всякий раз,
когда «возмущающая», функция
.
Такая ситуация имеет место всякий раз,
когда «возмущающая», функция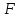 является
консервативной3.
В самом деле, пусть
является
консервативной3.
В самом деле, пусть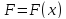 тогда:
тогда:
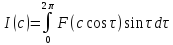 .
.
Функция
 четная периодическая функция
четная периодическая функция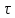 периода
периода .
Следовательно, она разлагается в ряд
Фурье, содержащий только
.
Следовательно, она разлагается в ряд
Фурье, содержащий только и следовательно, в силу ортогональности
и следовательно, в силу ортогональности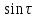 и
и для любого
для любого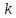 :
:
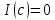 .
.
Условимся
в дальнейшем считать, что
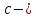 это
отличный от нуля корень уравнения (11)
кратности еденицы, могут быть рассмотрены
и более общие случаи. Однако при этом
может оказаться, что решение нельзя
представить в виде рядов (6); функция
это
отличный от нуля корень уравнения (11)
кратности еденицы, могут быть рассмотрены
и более общие случаи. Однако при этом
может оказаться, что решение нельзя
представить в виде рядов (6); функция должна быть представлена в виде ряда,
расположенного по дробным степеням
параметра
должна быть представлена в виде ряда,
расположенного по дробным степеням
параметра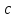 .
Тогда уравнение (12) определяет единственное
значение
.
Тогда уравнение (12) определяет единственное
значение .
Таким образом, на этом шаге алгоритм
позволяет определить амплитуду
порождающего решения и первую поправку
на частоту, т.е. полностью рассчитать
нулевое приближением. Если ограничиться
нулевым приближением, то мы получим
приближеное решение в виде:
.
Таким образом, на этом шаге алгоритм
позволяет определить амплитуду
порождающего решения и первую поправку
на частоту, т.е. полностью рассчитать
нулевое приближением. Если ограничиться
нулевым приближением, то мы получим
приближеное решение в виде:
 .
(13)
.
(13)
Вернемся
теперь снова к уравнению (8). Определив
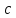 и
и
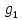 из уравнений (11) и (12), мы пришли к уравнению,
в котором правая часть
из уравнений (11) и (12), мы пришли к уравнению,
в котором правая часть это периодическая функция времени. Эта
функция обладает тем свойством, что она
не содержит первых членов разложения
в ряд Фурье4.
Уравнение (8) теперь можно переписать в
виде:
это периодическая функция времени. Эта
функция обладает тем свойством, что она
не содержит первых членов разложения
в ряд Фурье4.
Уравнение (8) теперь можно переписать в
виде:

где
 некоторые
известные числа.
некоторые
известные числа.
Его решение имеет вид:
 ,
(14)
,
(14)
где
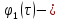 периодическая функция, разложение
которой не содержит
периодическая функция, разложение
которой не содержит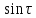 и
и
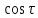 :
:
 .
.
Функция
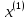 удовлетворяет условию:
удовлетворяет условию:
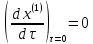 ,
,
которое
позволяет вычислить постоянную
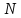 :
:
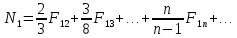 .
(15)
.
(15)
Постояная
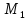 в этом приближении определена быть не
может. Следовательно, для того чтобы
определить решение с точностью до
членов, содержащих
в этом приближении определена быть не
может. Следовательно, для того чтобы
определить решение с точностью до
членов, содержащих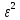 ,
необходимо рассмотреть второе приближение.
,
необходимо рассмотреть второе приближение.
Уранение
для
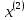 имеет вид:
имеет вид:
 ,
(16)
,
(16)
где

причем
 функция,
не содержащая величин
функция,
не содержащая величин
 и
и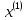 :
:
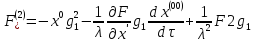 .
.
Здесь
 означает производную по аргумену
означает производную по аргумену . Функции
. Функции ,
,
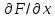 и
и
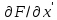 вычислены при
вычислены при .
.
Преобразуем
уравнение (16), заменив в нем величины
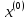 и
и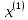 их выражениями (9) и (14):
их выражениями (9) и (14):
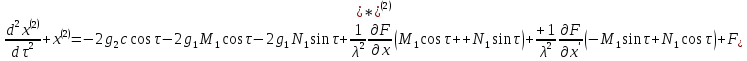 ,
(17)
,
(17)
где
 ,
,
является
известной функцией времени. Заметим,
что величина ,
входящая в уравнение (17), также известна;
она определяется формулой (15).
,
входящая в уравнение (17), также известна;
она определяется формулой (15).
Выпишем теперь условия существования периодических решений. Их можно представить в следующем виде:
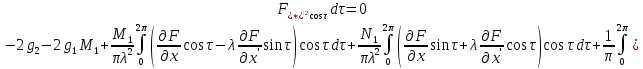 ,
,
 .
.
(18)
Преобразуем уравнение (18). Сначала рассмотрим второй интеграл, входящий в первое их этох уравнений, и проинтегрируем его по частям:

поскольку амплитуда с является корнем уравнения (11). Преобразуем теперь первый из интегралов, входящих в это уравнение:
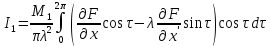 .
.
Для этого заметим сначала, что:
 ,
,
т.е
выражение
 можно переписать так:
можно переписать так:
 .
.
Рассмотрим теперь равенство (12) и перепишем его в следующей форме [3]:
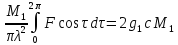 .
.
Дифференцируя это выражение по с, получим:
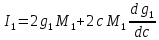 .
.
Таким образом, первое из уравнений (19) в окончательном виде будет иметь следующую форму:
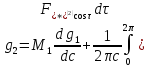 .
(19)
.
(19)
Преобразуем теперь второе уравнение (18). Прежде всего перепишем его в виде:
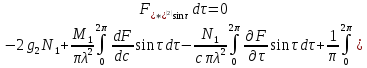 .
.
Используя (11), получим:
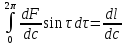 .
.
Далее
 .
.
Таким образом, в окончательном виде это уравнение будет иметь следующий вид:
 .
(20)
.
(20)
Так
как
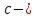 простой нуль функций5
простой нуль функций5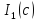 ,
то
,
то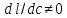 ,
и уравнение (16) определяет единственное
значение
,
и уравнение (16) определяет единственное
значение .
После определения
.
После определения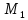 величина
величина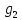 определяется также единственным образом
по формуле (19).
определяется также единственным образом
по формуле (19).
Определив
 и
и согласно (19) и (20), мы обеспечим разрешимость
уравнения (16):
согласно (19) и (20), мы обеспечим разрешимость
уравнения (16):
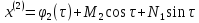 ,
,
где
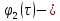 некоторая периодическая функция
некоторая периодическая функция периода
периода .
Постоянная
.
Постоянная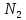 определяется из условия:
определяется из условия:
 .
.
Постоянная
 в этом приближении остается неопределенной.
Если мы хотим построить решение,
учитывающее второе прибижение, то нужно
рассмотреть также и третье приближение
и т.д.
в этом приближении остается неопределенной.
Если мы хотим построить решение,
учитывающее второе прибижение, то нужно
рассмотреть также и третье приближение
и т.д.
Легко
видеть, что этот процесс можно неограниченно
продолжить и вычислить любой член
разложения (10). Заметим, что только на
первом шаге нам приходится решать
нелинейное уравнение
 ,
которое имеет, вообще говоря, произвольное
количество решений. Но определив
амплитуду порождающего решения, мы в
дальнейшем имееем дело только с линейными
уравнениями и все остальные искомые
величины определяются однозначно.
Заметим еще, найденное решение
удовлетворяет следующим начальным
условиям:
,
которое имеет, вообще говоря, произвольное
количество решений. Но определив
амплитуду порождающего решения, мы в
дальнейшем имееем дело только с линейными
уравнениями и все остальные искомые
величины определяются однозначно.
Заметим еще, найденное решение
удовлетворяет следующим начальным
условиям:
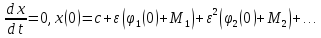 ,
,
где
 это корень уравнения
это корень уравнения .
Это решение при
.
Это решение при
 переходит в решение уравнения:
переходит в решение уравнения:
 ,
,
определенное начальными условиями:
 ,
,
т.е. в решение
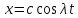 .
.
Ряды
(10), как это показал Пуанкаре, сходится
для достаточно малых значений параметра
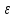 .
.
ПРИМЕР:
В качестве примера рассмотрим известное уравнение Ван дер Поля:
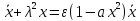 (21)
(21)
и построим его возможные периодические режимы в нулевом приближении. После преобразования (2) уравнение (21) примет вид:
 .
(22)
.
(22)
Разыскивая
решение в виде ряда (6), где функции
 удовлетворяют
условиям (5), мы найдем, что:
удовлетворяют
условиям (5), мы найдем, что:
 ,
,
а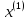 удовлетворяют
уравнению:
удовлетворяют
уравнению:
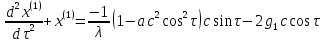 .
(22.1)
.
(22.1)
Раскладывая правую часть уравнения (22.1) в ряд Фурье получим:
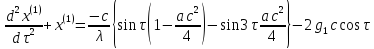 .
(23)
.
(23)
Для
того чтобы уравнение (23) имело периодические
решения периода
 ,
необходимо и достаточно, чтобы разложение
правой части в ряд Фурье не содержало
первых гармоник, т.е чтобы коэффициенты
при
,
необходимо и достаточно, чтобы разложение
правой части в ряд Фурье не содержало
первых гармоник, т.е чтобы коэффициенты
при и
и были равны нулю. Это дает два уравнения
для определения
были равны нулю. Это дает два уравнения
для определения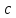 и
и ,
откуда:
,
откуда:

Таким образом, уравнение (22.1) имеет два стационарных режима:
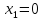 ,
,
 .
(24)
.
(24)
Первый
из стационарных режимов
 это
состояния покоя. Второй стационарный
режим
это
состояния покоя. Второй стационарный
режим это режим автоколебаний.
Мы видим,
что уравнение (21) допускает автоколебательный
режим только в том случае, когда
это режим автоколебаний.
Мы видим,
что уравнение (21) допускает автоколебательный
режим только в том случае, когда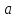 положительно.
положительно.
