Lektsii_Rubleva / Лекции Рублева-1 / Гл 07 _нтеграли залежн_ в_д параметра / Пар 7-3 Власн_ _нтеграли, залежн_ в_д параметра

3

Глава 7

Інтеграли, залежні від параметра

3. Власні інтеграли, залежні від параметра.

Нехай , де , , інтегрована за Ріманом на сегменті функція. Тоді на інтервалі визначимо функцію :

,

(1)

яку ми назвемо інтегралом Рімана, залежним від параметра (ІЗП).

Теорема 1.	(Неперервність ІЗП)
	Якщо функція неперервна на , то .

Доведення. Нехай - довільна точка цього проміжку, розглянемо звуження , де . З того, що - компакт - рівномірно неперервна на . Тому

, що й доводить неперервність в точці внаслідок довільності з цього й слідує, що .

Теорема доведена.

Наслідок.	(Граничний перехід у ІЗП)
	В умовах попередньої теореми має місце рівність: .

Теорема 2.	(Неперервність складної функції ІЗП)
	Якщо функція неперервна на , а функції , то функція
		(2)
	неперервна .

Доведення. Нехай - довільна точка цього проміжку. З адитивності інтегралу можемо записати:

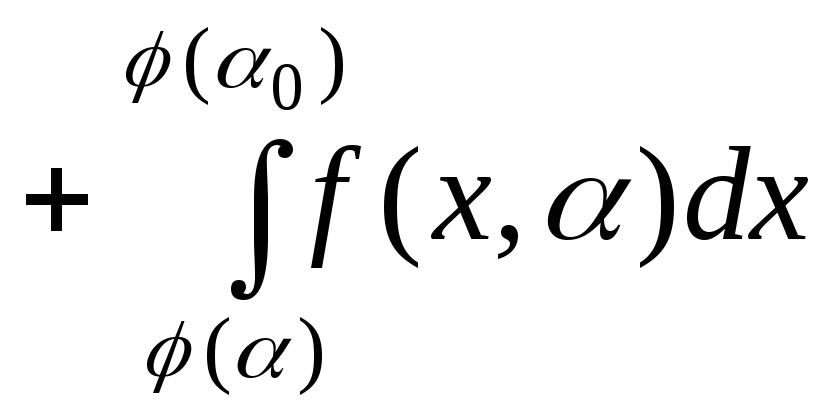. (3)

для першого доданку цієї формули застосуємо теорему 1, одержимо, що його границя при дорівнює . Для інших двох доданків застосуємо теорему про середнє, використавши неперервність функції :

, де - деяка середня точка між та . Тому при прямуванні внаслідок неперервності розглядуваних функцій одержимо, що , аналогічно з третім доданком формули (3). Тому при одержимо, що .

Теорема доведена.

Теорема 3.	(Диференційованість ІЗП)
	Якщо функція має на неперервну часткову похідну , то функція (з(1)) диференційована на і її похідна обчислюється таким чином:
		(4)
	(формула Лейбниця)

Доведення. За теоремою 1 є неперервною функцією на , треба довести диференційованість та рівність , це означає, що треба довести співвідношення:

(5)

Зафіксуємо довільне , і як в теоремі 1 виберемо сегмент , який містить і позначимо . З рівномірної неперервності на ми маємо, що : : .

Застосовуючи теорему про середнє, будемо мати, якщо :

, так як середня точка між і . Остаточно маємо:

,звідки і слідує рівність (5).

Теорема доведена.

Теорема 4.	(Диференційованість складної функції ІЗП)
	Якщо в умовах теореми 2 неперервна на разом із своєю похідною , а функції і диференційовані на і її похідна обчислюється за формулою:
		(6)

Доведення. Позначимо праву частину рівності (6) як і для довільної точки і : розглянемо приріст функції в точці та оцінимо вираз:

.

За попередньою теоремою першій доданок є , легко також оцінити два інших доданки: , де - проміжна точка, між та . З неперервності маємо:

при . Тоді маємо таку оцінку різниці:

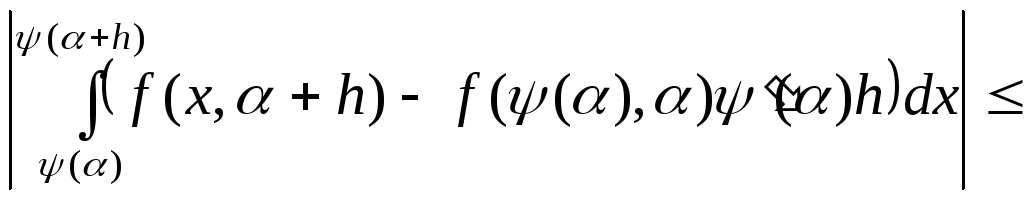
, аналогічно оцінюється третій доданок. Підсумовуючи все це маємо формулу (6).

Нехай тепер , , , тоді можна визначити неперервні функції , на своїх областях визначення. Позначимо:

,

.

Інтеграли називаються повторними.

Теорема 5.	(Інтегрування по параметру ІЗП)
	Якщо , то .

Доведення. Розглянемо дві функції:

, , , .

Легко побачити за теоремою 3, що , а також . З останньої умови та тотожності слідує рівність , а тому при маємо, що .

Теорема доведена.

Зауважимо, що усі наведені теореми цього розділу є лише достатніми умовами.