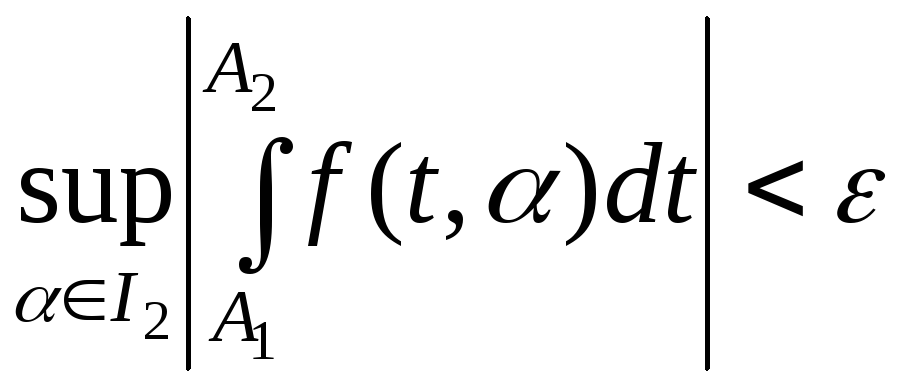Lektsii_Rubleva / Лекции Рублева-1 / Гл 07 _нтеграли залежн_ в_д параметра / Пар 7-4 Невласн_ _нтеграли 1 роду, залежн_ в_д параметра

3

Глава 7

Інтеграли, залежні від параметра

4. Невласні інтеграли 1 роду, залежні від параметра

Нехай , , , . Розглянемо інтеграл:

, , (1)

який називається невласним інтегралом першого роду, залежним від параметра (НІЗП).

Інтеграл називається збіжним на інтервалі (позначимо це таким чином , або ), якщо він збігається , тобто

. (2)

Якщо розписати означення границі за Коші, то одержимо:

: ,

або еквівалентне наведеному:

: . (3)

Збіжний на інтервалі інтеграл називається рівномірно збіжним на (позначимо це таким чином , або ), якщо

: , (4)

або аналогічно можна записати:

: , (5)

Теорема 1.	(Критерій Коші)
	Інтеграл збігається рівномірно на інтервалі тоді і тільки тоді, коли
	:	(6)

Доведення. Необхідність. Нехай рівномірно збігається, тобто для нього виконується умова (4), з неї слідує, що :

, .

Необхідність доведена.

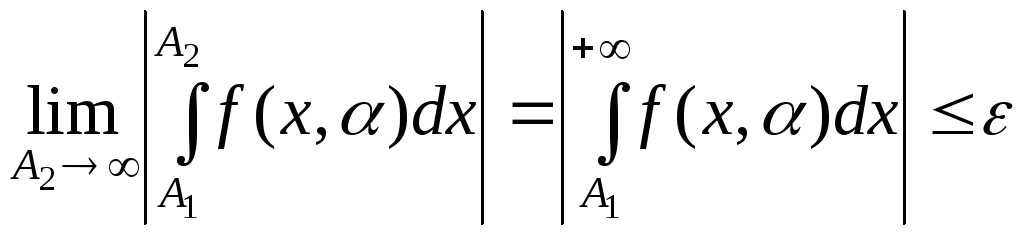
Достатність. Якщо виконується умова (6), з урахуванням збіжності маємо: . Тепер переходимо до супремуму по і маємо потрібне, враховуючи що - довільне і .

Теорема доведена.

Теорема 2.	(Мажорантна ознака Вейєрштрасса)
	Для того, щоб інтеграл збігається рівномірно на інтервалі достатньо, щоб існувало таке число і така функція , що справджується нерівність та інтеграл був збіжним.

Доведення. За умовами теореми інтеграл збігається (за мажорантою ознакою при фіксованому ). Із збіжності інтегралу : , внаслідок чого збігається рівномірно.

Ознака доведена.

Теорема 3.	(Ознака Абеля)
	Якщо інтеграл збігається рівномірно на проміжку , а функція - обмежена, та монотонна по змінній , то інтеграл збігається рівномірно на .

Доведення. З рівномірної збіжності можемо записати критерій Коші: : , позначимо (при теорема очевидна). З монотонності та інтегрованості на проміжку запишемо другу теорему про середнє:

, а далі з критерію Коші все й слідує.

Теорема доведена.

Теорема 4.	(Ознака Діріхле)
	Якщо функція - монотонна по змінній , а також на проміжку , а функція - обмежена на , то інтеграл збігається рівномірно на .

Доведення. З рівномірної збіжності можемо записати умову: : , позначимо (при теорема очевидна). З монотонності та інтегрованості на проміжку запишемо другу теорему про середнє:

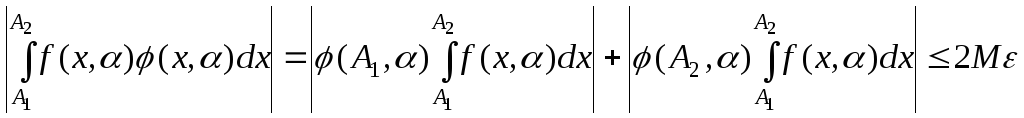, а далі з критерію Коші все й слідує.

Теорема доведена.

Теорема 5.	(Ознака Діні)
	Нехай , , , , , - невід’ємна і збігається інтеграл , причому - неперервна на функція. Тоді інтеграл рівномірно збігається на .

Без доведення.