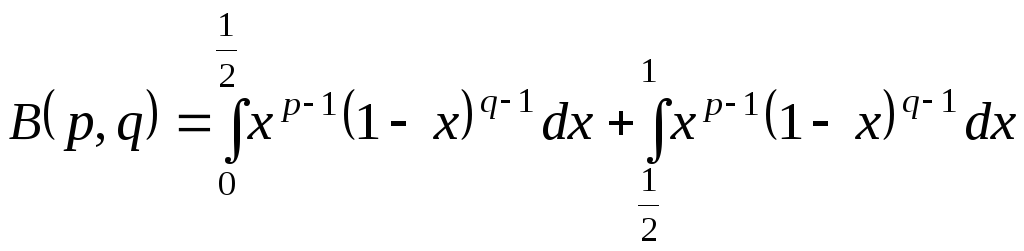Lektsii_Rubleva / Лекции Рублева-1 / Гл 07 _нтеграли залежн_ в_д параметра / Пар 7-8 Ейлеров_ _нтеграли

4

Глава 7

Інтеграли, залежні від параметра

8. Ейлерові інтеграли

(1)

,

(2)

які називаються відповідно ейлеревими інтегралами першого та другого роду, або бета-функцією та гама-функцією.

Розглянемо , розділивши дві особливості, а саме – точки та .

(3)

В околі нуля , тому збігається, коли ,а збігається існує при .

Якщо розглянути , то , а інтеграл від функції в правій частині останньої рівності існує, то рівномірно збігається на розглянутому проміжку, тобто є неперервною на будь-якому додатному сегменті , в наслідок довільності та будемо мати, що неперервна .

Аналогічно, розглянувши інтеграл бачимо, що він рівномірно збігається на будь-якому проміжку , де . Звідки слідує існування та неперервність , і так само похідної довільного порядку.

Розглянемо :

(4)

- формула доведення, або основне функціональне рівняння для функції .

Маючи , одержимо, що

(5)

Щоб уявити собі графік , розглянемо другу похідну , з чого слідує, за теоремою Ролля, що має не більше, як один нуль, в якому має мінімум. Цей нуль знаходиться на , крім того, з співвідношення: , так як .

Похилих асимптот нема (без доведення).

Продовжимо формулу (4) :

(5)

З останньої формули спробуємо продовжити на від’ємну частину дійсної осі, з викинутими цілими від’ємними значеннями , , покладаючи:

, ,

(6)

якщо , то і формула (6) має зміст. Легко побачити, що функція, визначена формулою (6) задовольняє основне функціональне рівняння (4) і набуває значення 1 при .

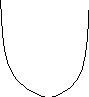
- вертикальні асимптоти, крім того, функція в правосторонньому околі точки має знак , то на , на , на і т.д. крім того , то маємо відповідну опуклість при . Далі без подальшого доведення намалюємо графік при всіх :

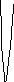
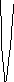
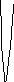
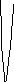
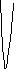
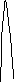
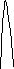
перейдемо до дослідження функції . Інтеграл (1) стає невласним в точках та , якщо . Розіб’ємо його на два:

(7)

Коли ∼0 збіжний при і коли ∼

збіжний при . З цього слідує, що існує у відкритому квадранті . Взявши довільні , і розглянувши область , одержимо, що , тобто інтеграл (1) збігається рівномірно, з чого слідує неперервність .

Властивості функцій та .

Властивість 1.	- очевидна	(8)
Властивість 2.		(9)
Доведення.	(9)

Аналогічно має місце.

					(10)
Властивість 3.					(11)
Доведення.				, зробимо заміну змінної ,:. Покладемо : . Помножимо на та проінтегруємо по в межах від 0 до :
					(12)

Якщо в інтегралі (1) зробити заміну змінної за формулою , одержимо:

(13)

Або аналогічно:

(14)

Тобто ліва частина (12) є . Обчислимо праву частину:

(15)

Залишилося переконатися, що заміна порядку інтегрування можлива:

а)	і неперервна в квадранті
б)	є неперервна функція при
в)	є неперервна функція при
г)	існує внаслідок його безпосереднього обчислення.

Властивість 4.
		(16)
		(17)
Властивість 5.		(18)

Доведення. З інтеграла Пуассона:

Властивість доведена.

Властивість 6.	Формула Лежандра.	(19)
Властивість 7.	ейлерова формула доповнення.	(20)