Lektsii_Rubleva / Лекции Рублева-1 / Гл 07 _нтеграли залежн_ в_д параметра / Пар 7-7 Деяк_ важлив_ _нтеграли, залежн_ в_д параметра

2

Глава 7

Інтеграли, залежні від параметра

7. Деякі важливі інтеграли, залежні від параметра

Випишемо спочатку ті, які будемо розглядати:

Інтеграл Діріхле		(1)
Інтеграл Пуассона		(2)
Інтеграл Френеля		(3)
Інтеграл Фруллані	Нехай , а інтеграл збігається . Тоді має місце рівність:
	,	(4.1)
	яку називають формулою Фруллані.
	Якщо та , то формула Фруллані набуває вигляду:
		(4.2)

Розглянемо більш детально перші два з них.

Інтеграл Діріхле: , легко бачити, що він збігається за ознакою Діріхле. Для його обчислення розглянемо інтеграл:

, . Оскільки функція , де 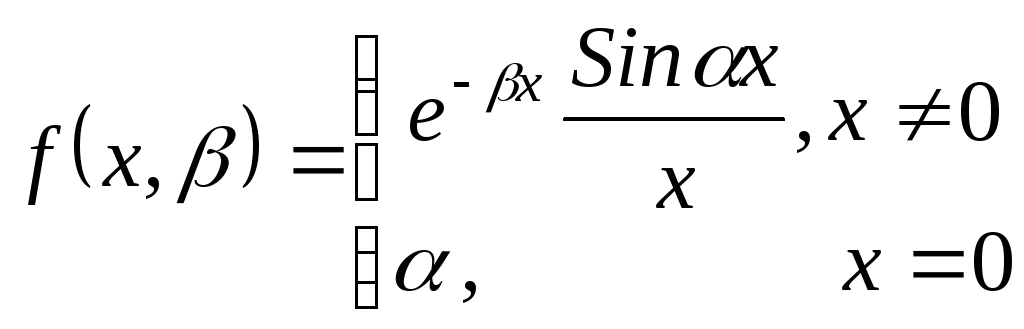, неперервна на , а збігається рівномірно (за ознакою Абеля) на , то - неперервна на і тому

(5)

Нехай . Тоді функція , за ознакою Вейерштрасса по параметру , то , згідно теореми про диференціювання НІЗП має місце рівність

, , .

(6)

Після інтегрування, одержимо:

,

і остаточно з урахуванням (6), маємо:

.

Інтеграл Пуассона

Його збіжність очевидна за ознакою Вейерштрасса. Після підстановки , , отримуємо: . Помножимо обидві частини останньої рівності на і про інтегруємо по одержаний результат в межах .

(7)

Функція , неперервна і невід’ємна. Функції , ;

, є неперервними, і нарешті, оскільки інтеграли , існують, то за теоремою про інтегрування в невласному розумінні НІЗП вони дорівнюють один одному:

,

(8)

звідки і маємо остаточний результат (2).

Інтеграл Фруллані. Розглянемо функцію , , яка за умовою має скінчену границю . Тоді маємо

, аналогічно , а тому . Згідно першої теореми про середнє 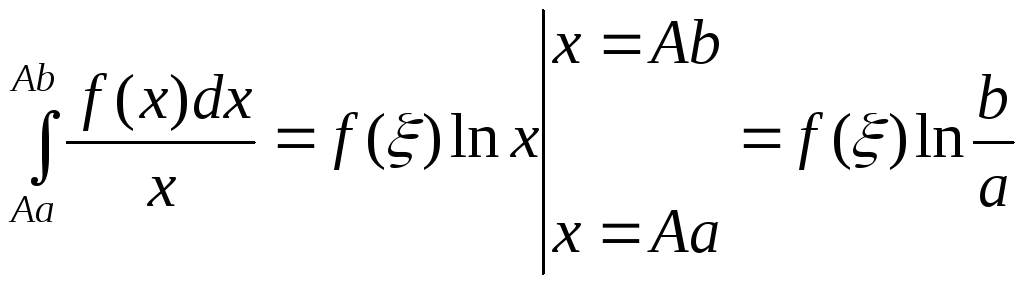, де - точка між та . З неперервності функції існує , а тому також існує

, формула (4.1) доведена.

Для другої частини розглянемо інтеграл на проміжку :

,

, де точки - визначені на відповідних проміжках. Зробимо граничний перехід при та знайдемо, що справджується формула (4.2).