Lektsii_Rubleva / Лекции Рублева-1 / Гл 07 _нтеграли залежн_ в_д параметра / Пар 7-2 Невласн_ _нтеграли другого ряду

2

Глава 7

Інтеграли, залежні від параметра

2. Невласні інтеграли другого ряду.

Нехай , і особлива точка функції . Нехай необмежена на , але обмежена на і . Позначимо , то називається інтегрованою за Ріманом на проміжку , а число її невласним інтегралом другого роду. Тоді невласний інтеграл позначають і називають збіжним, інакше він називається розбіжним.

Теорема 1.	(Критерій Коші)
	існує : : , виконується нерівність .

Теорема 2.	(Практична ознака збіжності)
	Нехай , . Якщо : , то -збіжний. Якщо : не існує.

Повністю аналогічно до рядів та невласних інтегралів першого роду визначається поняття абсолютної та умовної збірностей невласного інтеграла 2 роду, а також зв’язок між цими збіжностями.

Заміною невласний інтеграл другого роду зводиться до невласного інтегралу першого роду.

Аналогічно визначається інтеграл для особливої точки .

Якщо у інтеграла 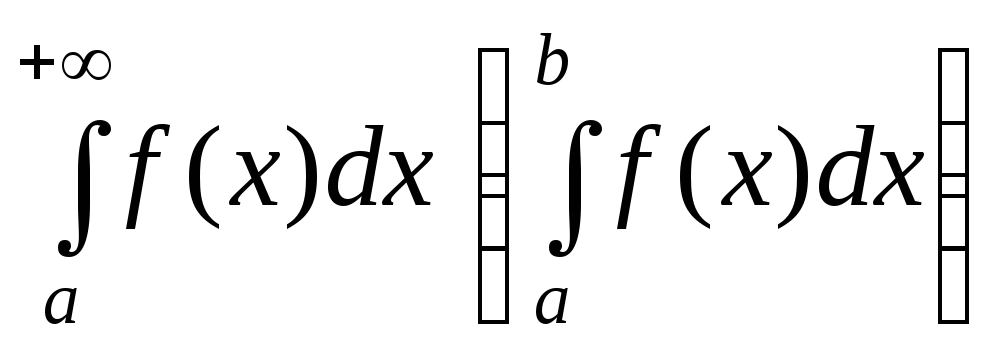скінчена кількість особливих точок , то розбиваємо його на скінчену кількість інтегралів, кожен з яких має особливість в лівій чи правій точці проміжку (але не в обох) і кажемо, що він збіжний (існує), якщо збіжний кожний з менших інтегралів.

Приклад 1.	Дослідити на збіжність інтеграл для функції .
	і вказаний інтеграл збігається тоді і тільки тоді, коли збігається кожний з наведених доданків.

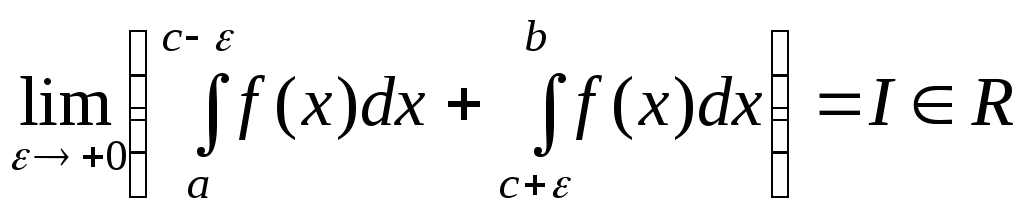Нехай , функція інтегрована , та інтеграл розбігається, але існує , то цю границю називають головним значенням у розумінні Коші розбіжного інтеграла і позначають .