Файловый архив студентов. Файловый архив студентов.
1259 вузов, 4592 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Киевский национальный университет им. Т. Шевченко
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

6_Dynamika tverdogo tila

.pdf
Скачиваний:
10
Добавлен:
19.03.2015
Размер:
1.13 Mб
Скачать
☆

223

який ставить у відповідність вектору кутової швидкості тіла вектор власного моменту імпульсу тіла. Такий запис дуже зручний, оскільки він не потребує вказівки на ту чи іншу систему координат. З

цієї точки зору він є повністю аналогічним запису рівнянь у векторній формі, який ми вже широко використовували у попередніх розділах. Необхідно звернути увагу на те, що так звана тензорна розмірність лівої і правої частин рівняння (6.24) однакова: і в лівій і в правій частинах маємо тензори одного й того ж самого рангу – першого, тобто вектори, оскільки, як уже було сказано, результатом

дії оператора ˆ , що є тензором другого рангу, на вектор є вектор.

I

6.4. Основні властивості тензора інерції та обчислення його компонент

Із явного вигляду головних моментів інерції абсолютно твердого тіла

n

n

 

n

 

I1 mi ( yi2 zi2 ) ,

I2 mi (xi2 zi2 ) ,

I3 mi (xi2 yi2 )

(6.25)

i 1

i 1

 

i 1

 

можна зробити очевидний висновок,

що всі вони додатно визначені, I1 , I2 , I3 0 ,

а також, що

жоден головний момент інерції не може бути більшим за суму двох інших головних моментів інерції.

Наприклад,

n

n

n

n

I1 I2 mi ( yi2

zi2 ) mi (xi2

zi2 ) mi (xi2 yi2 2zi2 ) I3

mi (xi2 yi2 ) . (6.26)

i 1

i 1

i 1

i 1

Легко бачити, що при всій різноманітності твердих тіл за їх формою та розподілом маси

(густини) тензори інерції, що характеризують їх інерційні властивості щодо обертання поділити на три групи:

1. Якщо всі три головні моменти інерції абсолютно твердого тіла різні, тобто I1 I2 I3 I1 ,

то про таке тіло кажуть, що воно за своїми інерційними властивостями щодо обертання являє собою так звану несиметричну дзиґу;

2. Якщо два з трьох головних моментів інерції абсолютно твердого тіла однакові, наприклад,

I1 I2 I3 , то про таке тіло кажуть, що воно за своїми інерційними властивостями щодо обертання

являє собою симетричну дзиґу;

3. Якщо всі три головні моменти інерції абсолютно твердого тіла однакові, I1 I2 I3 , то таке

тіло за своїми інерційними властивостями щодо обертання являє собою сферичну дзиґу.

224

Співвідношення між головними моментами інерції абсолютно твердого тіла тісно пов’язані з

його симетрією (Рис. 6.6).

а)

I1≠I2≠I3≠I1

 

Найнаочнішим прикладом сферичної

 

 

дзиґи може бути власне сфера (сферична

 

 

 

1

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

оболонка), звідки й походить сама назва, або

 

 

 

 

 

 

 

I3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

будь-яке тіло, що має сферичну (або

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

центральну)

симетрію: суцільна

 

однорідна

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

O

 

y

 

 

куля ( const) , а також будь-яке тіло зі

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

сферично симетричним розподілом густини

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I2

 

 

 

 

(r)

 

(густина

залежить

лише

від

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I1x + I2y + I3z

=1

відстані до центру сфери) . Менш очевидним

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I1<I2<I3

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

є той факт, що властивостями сферичної

 

 

I1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

дзиґи володіють однорідний куб та тетраедр,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

оскільки в силу їх симетрії для кожного з них

б)

I1=I2≠I3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

можна

вказати

3

еквівалентні

взаємно

 

 

 

 

 

 

z

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

перпендикулярні осі, моменти інерції

 

 

 

 

 

 

 

 

 

I3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

відносно яких однакові.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Прикладом симетричної дзиґи може

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

бути добре відома всім з дитинства іграшка –

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

дитяча дзиґа, яка має осьову (аксіальну)

 

 

 

 

 

 

 

O

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

зовнішню симетрію і аксіально симетричний

 

 

 

1

 

 

 

 

 

 

 

 

 

 

I1(x2+ y2)+ I3z2=1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

розподіл густини.

 

 

 

 

 

 

 

 

 

 

 

 

 

I1

 

 

 

 

 

 

 

 

 

 

I1=I2>I3

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ясно, що властивості симетричної

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

дзиґи мають всі однорідні геометричні тіла

в)

I1=I2=I3=I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

обертання:

круглий

циліндр,

 

прямий

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

круговий конус, еліпсоїд обертання тощо.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Взагалі,

 

можна

показати,

що

 

будь

яке

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

однорідне

тіло,

що має одну вісь симетрії

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

порядку

 

вище

 

4

, є

симетричною

 

 

 

 

O

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

третього

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

дзигою.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I(x2+ y2+z2)=1

 

 

Важливим

частинним

 

випадком

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

симетричної дзиґи є так званий ротатор

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

система

матеріальних

точок,

що

лежать

на

Рис. 6.6. Зв’язок між симетрією абсолютно

твердого тіла та тензором інерції

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4 Порядком осі симетрії називають число n , яке показує, при якому найменшому куті повороту 2 n навколо цієї осі , геометрична фігура суміщається сама з собою.

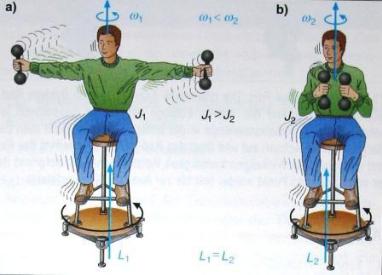
225

одній прямій, відстань між якими не змінюється в процесі руху. вважати, що ці точки з’єднані нерозтяжним і невагомим стержнем). При прийнятому нами виборі системи координат для всіх

 

 

 

n

 

частинок ротатора xi yi

0 , отже,

I1 I2

mi zi2 ,

I3 0 . Модель ротатора, що складається з

 

 

 

i 1

 

двох матеріальних точок, широко застосовується при описі властивостей двоатомних молекул.

Нарешті, всі низькосиметричні тіла, тобто такі, серед елементів симетрії яких є лише площини симетрії та осі поворотів на кут , при яких тіло суміщається саме з собою, мають всі властивості асиметричної дзиґи. Прикладом може бути звичайна цеглина, що являє собою прямий однорідний паралелепіпед загального вигляду. Переважна більшість оточуючих нас предметів за своїми інерційними властивостями щодо обертання є асиметричні дзиґи.

Тіло людини також має три різні за величиною головні моменти інерції (ясно, що йдеться про манекени або про випадки, коли при виконанні різних вправ у гімнастиці, стрибках у воду, фігурному катанні тощо спортсмен фіксує і підтримує незмінною протягом певного часу конфігурацію свого тіла, так, що його можна вважати твердим). Спортсмени, танцюристи, артисти цирку часто використовують зміну моменту інерції

власного

тіла

для уповільнення

або прискорення обертання, як правило, широко розкидаючи руки або

притискаючи їх до тулуба. Це дуже добре

 

видно демонстраційних дослідах з лавою

 

Жуковського (Рис. 6.7).

Оскільки величина

 

моменту

імпульсу

L Lz

направленого

 

вздовж

осі

обертання

залишається

 

незмінною, то зміна моменту інерції від I1

 

до I 2

призводить

до

зміни

кутової

 

швидкості обертання від 1

до 2 , так як

 

L I1 1

I2 2 const . Причому, якщо

 

I1 I2 , то 1 2 .

 

 

 

 

Нарешті

варто

відзначити

 

поширений

випадок

 

розташування

Рис. 6.7

 

 

частинок твердого тіла в одній площині. Якщо обрати декартову прямокутну систему координат так,

щоб вісь OZ була перпендикулярна до вищезгаданої площини, то для всіх частинок zi

0 . Тоді

нерівність (6.26) переходить у рівність

 

 

 

n

n

n

 

 

I1 I2 mi yi2

mi xi2

mi (xi2 yi2 ) I3 ,

 

(6.27)

i 1

i 1

i 1

 

 

тобто сума двох головних моментів інерції відносно осей, що лежать в площині тіла,

дорівнює

моменту інерції відносно осі перпендикулярної до вищезгаданої площини, I1 I2

I3 .

 

 

 

 

 

 

 

 

 

 

 

226

Обчислення

компонент

тензора

інерції

 

 

 

 

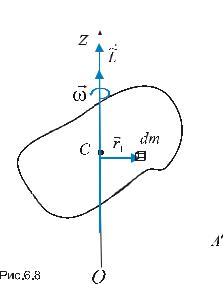
Розглянемо процедуру обчислення компонент тензора

 

 

 

 

інерції на простому прикладі однорідного прямого

 

 

z

 

паралелепіпеда

зі

сторонами

a, b, c

і

густиною

 

 

 

 

const.

 

 

 

 

 

 

 

 

 

 

Із міркувань симетрії оберемо прямокутну

 

 

 

 

декартову систему

координат

з

початком

в центрі

 

 

c

 

паралелепіпеда (в точці перетину його просторових

 

 

O

y

 

 

 

діагоналей) і з осями, спрямованими вздовж осей

 

 

 

 

симетрії паралелепіпеда, як це

показано

на Рис. 6.8.

x

 

b

 

 

 

 

 

 

 

 

 

 

Можна очікувати,

що така система координат буде

 

a

Рис. 6.8.

 

 

 

 

 

 

 

 

 

 

 

власною системою координат тензора інерції паралелепіпеда. Це підтверджується прямим

обчисленням недіагональних компонент тензора інерції за формулою (6.22). Наприклад,

 

 

 

 

 

a 2

b 2

c 2

 

I xy xydV xdx

ydy

dz 0 ,

(6.28)

 

V

 

a 2

b 2

c 2

 

оскільки визначені інтеграли від непарних функцій на симетричних межах завжди

дорівнюють нулю

 

 

 

 

 

a 2

 

x2

 

a 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xdx

 

0 .

 

 

(6.29)

 

 

 

a 2

2

 

a 2

 

 

 

 

 

 

 

 

 

Залишається обчислити три діагональних (головних) моменти інерції.

Наприклад, момент інерції відносно осі OX є

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a 2

b 2

c 2

 

 

a 2

b 2

c 2

I1 I xx ( y2 z2 )dV [ y2dV z2dV ] [ dx y2dy dz

 

dx dy z2dz]

 

 

 

 

V

 

 

 

 

 

 

 

V

 

 

 

 

V

 

a 2

b 2

c 2

 

 

a 2

b 2

c 2

 

 

 

a 2 y3

 

b 2

 

c 2

 

a 2

 

b 2

z3

 

c 2

 

b3

c3

 

1

 

[b2

c2 ]

 

 

 

 

 

 

 

 

x

 

 

 

 

z

 

x

 

y

 

 

 

 

 

a

 

c ab

 

 

abc

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a 2 3

 

 

 

c 2

 

a 2

 

b 2

3

 

 

 

 

3 4

3 4

 

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b 2

 

 

 

 

 

 

 

 

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

V [b2 c2

] .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(6.30)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Аналогічно обчислюються і моменти інерції відносно I2

I yy

та I3 I zz .

 

 

Остаточно маємо три головні моменти інерції однорідного прямого паралелепіпеда:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

227

I

 

 

 

1

M [b2 c2 ] ,

I

 

 

 

1

M [a2 c2 ] ,

I

 

 

 

1

M [a2 b2 ] .

(6.31)

1

12

2

12

3

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Якщо a b c , то, як це показано на Рис.6.1, I3 I2 I1 .

Якщо c b a , то маємо пряму призму з квадратною основою, для якої

I

 

I

 

 

 

1

M [a2 c2 ] ,

I

 

 

 

1

M [a2 b2

] ,

(6.32)

1

2

12

3

12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

тобто така призма являє собою симетричну дзиґу.

 

 

При a b c маємо куб, для якого всі три головні моменти інерції однакові,

 

I

 

I

 

I

 

 

1

Ma2 ,

 

 

 

 

 

 

 

(6.33)

1

2

3

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

і який, таким чином, за своїми інерційними властивостями щодо обертання являє собою

сферичну дзиґу.

Будь-яке тіло, яке має так само як і куб 3 взаємно перпендикулярні осі симетрії четвертого

порядку, є сферичною дзигою.

Із виразів (6.32) можна отримати корисну формулу для головного моменту інерції

однорідного тонкого стержня довжиною

l a,b відносно осі,

перпендикулярної до стержня.

Враховуючи, що l c ,

і нехтуючи величинами a2 , b2 порівняно з c2 одержимо

I

 

I

 

 

1

Ml 2 .

 

 

(6.34)

1

2

 

 

 

 

 

12

 

 

 

 

 

 

 

 

 

 

 

 

Таким чином, для тонкого стержня

I1 I2 , I3 0 , тобто він має властивості ротатора.

Еліпсоїд інерції.

Якщо наочним

геометричним образом

вектора є направлений відрізок

(стрілка) певної довжини, то для унаочнення тензора інерції (його зовнішньої симетрії)

використовують геометричну побудову, яку називають еліпсоїдом інерції. Рівняння еліпсоїда інерції у власній системі координат тензора інерції має вигляд

I

x2 I

2

y2 I

3

z2

1.

(6.33)

1

 

 

 

 

 

Його можна переписати у вигляді

 

 

x2

 

 

 

 

 

y2

 

 

 

 

 

z2

 

 

 

1

,

(6.34)

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

 

2

1

 

 

 

1

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I2

 

 

 

 

 

 

I3

 

 

 

 

 

 

 

 

I1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

228

звідки ясно видно, що довжина півосей еліпсоїда інерції обернено пропорційна кореню квадратному з відповідних числових значень головних моментів інерції5. На Рис.6.6 зображено прямий однорідний паралелепіпед, пряму призму з квадратною основою та куб, для яких вище було розраховано головні моменти інерції разом із відповідними еліпсоїдами інерції. Можна помітити, що еліпсоїди інерції певною мірою передають співвідношення розмірів цих однорідних тіл. Наприклад, найдовшій стороні прямого паралелепіпеда відповідає найдовша піввісь еліпсоїда інерції, а найкоротшій стороні

найкоротша піввісь еліпсоїда інерції. Еліпсоїд інерції можна розглядати як однорідне тверде тіло,

інерційні властивості якого ідентичні інерційним властивостям твердого тіла.

Оскільки еліпсоїд інерції нерухомий відносно тіла, то аналіз руху тіла можна звести до

аналізу руху його еліпсоїда інерції, і абстрагуватися, таким чином, від конкретної форми твердого тіла. Наприклад, напрям вектора моменту імпульсу абсолютно твердого тіла при обертанні навколо довільної осі, що проходить через його центр мас, можна знайти за допомогою побудови,

запропонованої Пуансо: будують площину дотичну до поверхні еліпсоїда інерції в точці її перетину з

віссю обертання (вектором кутової швидкості ) і з центру еліпсоїда опускають на неї

перпендикуляр, напрям якого вказує напрям вектора моменту імпульсу L ( Рис.6.9).

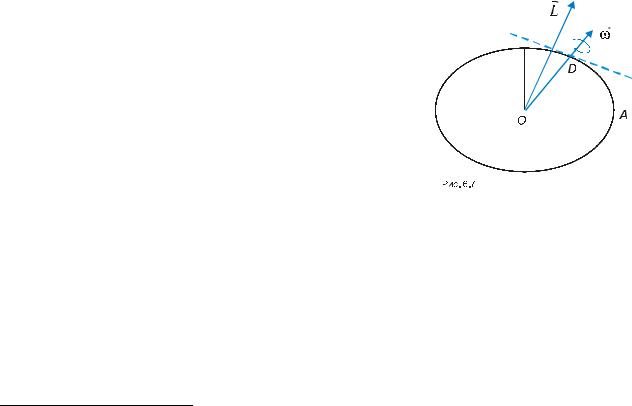
Момент інерції абсолютно твердого тіла відносно будь-якої осі, що проходить через центр його мас, може бути знайдений за довжиною

відрізка OD , що з’єднує центр еліпсоїда інерції O з точкою D , в якій

 

 

ця вісь перетинає поверхню еліпсоїда інерції (Рис.6.9). Для цього треба

 

 

розглянути переріз еліпсоїда інерції, який містить відрізок OD та одну з

 

 

головних осей еліпсоїда інерції. Нехай, наприклад, це буде одна із

 

 

головних осей інерції, що перетинає поверхню еліпсоїда інерції в точці

 

 

Рис. 6.9.

 

 

 

 

 

 

 

A і момент інерції відносно якої є I1 . Тоді момент інерції IOD відносно осі OD можна визначити за

формулою I

OD

I

1

(OA / OD)2 .

 

 

 

 

 

 

 

6.5. Кінетична енергія абсолютно твердого тіла

Кінетична енергія абсолютно твердого тіла як і будь-якої системи частинок може бути подана

~

у вигляді суми кінетичної енергії руху системи як цілого та власної кінетичної енергії T :

5 Оскільки йдеться про геометричну побудову, то розмірність головних моментів інерції не беруть до уваги.

MVc2 ~

T T .

2

Обчислимо власну кінетичну енергію абсолютно твердого тіла:

~

n

m 2

 

1

n

 

 

 

1

n

 

 

 

1

n

 

T

 

i i

 

 

mi

(i

i

)

 

mi

([ ri

] i

)

 

mi (

2

 

 

 

 

i 1

 

2 i 1

 

 

 

2 i 1

 

 

 

2 i 1

 

229

(6.35)

n

[ri i ]) 2 i 1 mi [ri i ])

При перетвореннях правої частини здійснено циклічну перестановку у мішаному векторному

~

добутку. Остаточно, враховуючи, що в отриманому виразі сума є власний момент імпульсу L , маємо

~

 

 

~

 

 

 

L

.

(6.36)

T

 

2

 

 

 

 

 

 

 

 

 

~

після підстановки в неї виразу (6.24) для

Формула (6.36) для власної кінетичної енергії T

 

 

 

 

~

 

власного моменту імпульсу абсолютно твердого тіла L набуває вигляду

~

 

ˆ

 

 

 

 

I

 

.

(6.37)

T

2

 

 

 

 

 

 

Власна кінетична енергія абсолютно твердого тіла (6.36) може бути також подана у декартових координатах як

~

 

1

3

 

 

 

 

 

1

 

3

 

3

 

 

 

 

 

1

3

 

 

 

 

T

 

 

 

 

L

 

 

 

 

 

 

I

 

 

 

 

 

I

 

 

 

(6.38)

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

 

1

 

 

 

 

 

 

1

 

1

 

 

 

 

 

, 1

 

 

 

 

або

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

1

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

T

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(6.39)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

, 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У головній системі координат тензора інерції

 

 

 

 

~

 

1

 

2

 

 

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

T

 

 

(I1 x

I 2 y

I3 z ) .

 

 

 

 

 

 

 

 

 

 

(6.40)

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

З цієї формули видно, що кінетична енергія, пов’язана з обертанням твердого тіла навколо будь-якої головної осі тензора інерції пропорційна відповідному головному моменту інерції і квадрату кутової швидкості обертання навколо цієї осі.

Для сферичної дзиґи кінетична енергія обертання навколо осі, що проходить через центр мас, є

~

 

I 2

 

T

 

,

(6.41)

2

де I головний момент інерції тіла, 2

квадрат кутової швидкості.

230

Для симетричної дзиґи кінетична енергія обертання навколо осі, що проходить через центр мас,

~

 

1

 

 

2

2

1

 

2

 

 

T

 

 

 

I1

( x

y )

 

I

3 z

,

(6.42)

2

2

і, зокрема, для частинного випадку ротатора,

 

~

 

1

 

 

2

2

 

 

 

 

 

T

 

 

 

I1

( x

y ) .

 

 

 

 

(6.43)

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вираз для кінетичної енергії абсолютно твердого тіла (6.35) в загальному випадку можна подати у вигляді суми шести доданків, три перших з яких відповідають трьом поступальним ступеням вільності, а три останніх трьом обертальним ступеням вільності:

T

1

MV 2

 

1

MV 2

 

1

MV 2

 

1

I 2

 

1

I 2

 

1

I 2

(6.44)

 

 

 

 

 

 

 

2 x

 

2 y

 

2 z

 

2 1 x

 

2 2 y

 

2 3 z

 

Для частинного випадку жорсткого ротатора маємо лише 5 ступенів вільності (3 поступальних і

2 обертальних) і, відповідно до цього, на один доданок менше в формулі (6.44).

6.5. Динаміка обертання твердого тіла навколо нерухомої осі

Важливим частинним випадком динаміки твердого тіла є його обертання навколо

нерухомої осі. Оскільки єдиною характеристикою такого руху є вектор кутової швидкості ,

який направлений вздовж осі обертання, будемо спочатку вважати, що вісь обертання проходить через центр мас

твердого тіла C (Рис.6.10). Оберемо систему координат, одна

з осей якої, наприклад, OZ співнапрямлена з вектором . При

такому виборі системи координат x y 0 і проекція

z повністю визначає проекцію вектора моменту

 

~

 

 

 

 

 

імпульсу Lz

(див. третє з рівнянь (6.15)):

 

 

 

 

 

 

 

 

~

 

 

 

 

 

 

 

 

 

 

 

 

I zz z .

 

Рис. 6.10.

 

 

Lz

(6.45)

 

 

 

 

 

 

Скалярну величину I zz у випадку обертання твердого тіла навколо нерухомої осі називають

моментом інерції (тіла) відносно осі. Момент інерції відносно осі, що проходить через центр мас

твердого тіла C , ми позначатимемо через IC , тобто у нашому випадку I zz IC .

~

IC

 

Lz

(6.46)

231

Проекція рівняння моментів (6.2) на вісь

OZ є

~

 

 

 

 

 

dLz

M

 

,

(6.47)

 

 

z

 

dt

 

 

 

 

 

 

де M z проекція сумарного моменту сил, прикладених до абсолютно твердого тіла, на вісь

обертання. Її називають моментом сил відносно осі обертання. Після підстановки (6.46) до (6.47)

одержимо основне рівняння динаміки обертання твердого тіла навколо нерухомої осі

I

 

d

M

 

або I

M

 

,

(6.48)

C

 

z

z

 

dt

C

 

 

 

 

 

 

 

 

 

 

 

Зцього рівняння видно, що момент інерції твердого тіла відносно осі повністю визначає інерційні властивості твердого тіла щодо обертання навколо цієї осі. Рівняння (6.48) за формою подібне до основного рівняння динаміки матеріальної точки, де інерційні властивості визначаються масою, яка є коефіцієнтом при прискоренні.

Зпопереднього ясно, що при прийнятому нами виборі системи координат, момент інерції відносно осі обертання може бути знайдений за формулою

IC Izz (x2 y2 )dV ,

(6.49)

V

 

яку можна подати у безкоординатному вигляді

 

IC r 2dV ,

(6.50)

V

 

де введено позначення r 2 (x2 y2 ) відстань від точки твердого тіла до осі обертання.

Таким чином, момент інерції твердого тіла відносно деякої осі повністю визначається розподілом мас у твердому тілі відносно цієї осі. Цілком зрозуміло, що

моменти інерції одного й того ж самого твердого тіла

Рис. 6.11.

визначені відносно різних осей будуть, у загальному випадку, різні.

Цілком зрозуміло, що обертання твердого тіла не завжди відбувається навколо осі, яка проходить через його центр мас. Більше того, на практиці у багатьох випадках здійснення саме такого обертання становить складну технічну задачу. У випадку, коли вісь обертання не проходить через

232

центр мас твердого тіла, можна скористатися загальним рівнянням моментів визначених відносно точки, що лежить на цій осі обертання (див рівняння (5.95))

dLdt M зовн ,

в якому, відповідно до викладеного в 5.3.1, момент імпульсу можна подати як

~

L L [RC P] ,

а момент зовнішніх сил як

 

 

 

 

 

~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M зовн M зовн

[R

 

F зовн ] .

 

 

 

 

 

 

 

 

 

 

(6.51)

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

Тепер розглянемо обертання твердого тіла навколо нерухомої

осі O A , яка паралельна

деякій осі, що проходить через центр мас тіла, і знаходиться на відстані

d від неї (Рис. 6.11). Тоді

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

 

~

 

~

 

~

 

 

 

 

 

 

 

 

 

 

 

 

L L [RC

P] L M[RC

RC ] L

M[RC [ RC ]] L M[RC

[ RC ]]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

~

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

L

M[ RC RC (RC

)] .

 

 

 

 

 

 

 

 

 

 

(6.52)

Проекція цього вектора на напрям осі обертання O A

(на вісь OZ ) є

 

 

LO A

Lz

~

 

 

 

2

 

)]

 

 

 

 

 

 

 

 

Lz

M [ RC ZC (ZC

 

.

 

 

 

 

(6.53)

Lz

M (RC

ZC ) IC Md

2

(IC Md

2

 

 

 

 

)

 

 

 

 

 

 

~

 

 

 

 

2

 

2

 

 

 

 

 

 

 

 

 

 

 

Останній вираз зручно подати у вигляді

 

 

 

 

 

 

 

L

I

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(6.54)

 

O A

 

 

O A

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

де введено момент інерції тіла відносно осі O A

 

 

 

 

 

 

 

I

O A

I

C

Md 2 .

 

 

 

 

 

 

 

 

 

 

 

 

 

(6.55)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Отримана формула (6.55) репрезентує дуже корисну в практичних застосуваннях теорему Гюйгенса-Штейнера: момент інерції твердого тіла відносно довільної осі є сума моменту

інерції тіла відносно паралельної осі, що проходить через центр мас тіла, та добутку маси тіла на квадрат відстані між цими осями.

Тепер для обертання твердого тіла навколо осі O A можна записати

IO A

d

M O A ,

(6.56)

 

dt

 

 

 

де M O A момент сил відносно осі обертання O A .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности