14.6. Многоконтурные системы с подчиненным регулированием координат электропривода

Для решения задач синтеза замкнутых систем электропривода, обладающих хорошим быстродействием и желаемым характером переходных процессов, разработан инженерный метод синтеза, получивший название метода последовательной коррекции с подчиненным регулированием координат или сокращенно метод подчиненного регулирования. В основе этого метода лежит разработка многоконтурных систем, когда в результате синтеза каждый из контуров описывается передаточной функцией второго или третьего порядка и обеспечивает оптимальное управление своей выходной регулируемой координатой.

Для построения такой системы в структурной схеме силовой части электропривода выделяют последовательность динамических звеньев, каждое из которых имеет на своем выходе соответствующую регулируемую координату - ток (I), скорость (), угол поворота () или путь (s). После этого синтезируют контуры регулирования, начиная с контура тока - первой внутренней координаты. Синтез обычно выполняется с использованием активных последовательных корректирующих звеньев (регуляторов), реализуемых на операционных усилителях постоянного тока с большим коэффициентом усиления.

Для решения задач синтеза замкнутых систем электро

В состав каждого контура входит объект регулирования с передаточной функцией W(p)_ор, апериодическое звено с малой постоянной времени W(p)_ и регулятор W(p)_рег. В результате образуется многоконтурная (2^х или 3^х-контурная) система подчиненного регулирования, построенная по иерархическому принципу, как показано на рис.14.10.

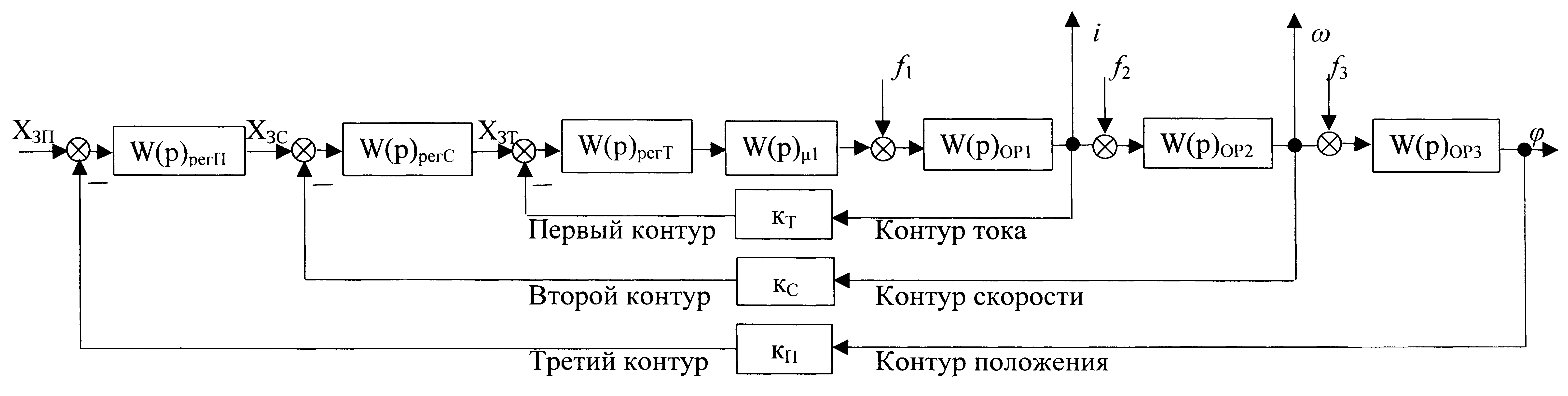
Рис.14.10. Трехконтурная система электропривода с подчиненным регулированием

I, ω, φ – регулируемые координаты, f1, f2, f3 – возмущения

14.7. Принципы оптимизации в системах подчиненного регулирования

При синтезе контуров регулирования используется два типа оптимальных настроек: настройка на модульный оптимум (МО) и настройка на симметричный оптимум (СО). Выбор типа настройки определяется требованиями к статическим и динамическим характеристикам при отработке управляющих воздействий и возмущений, действующих внутри контура регулирования.

Модульный оптимум настройки контуров регулирования

Считается, что замкнутый контур регулирования с единичной обратной связью настроен на модульный оптимум, если он имеет передаточную функцию второго порядка вида

, (14.8)

где: а_М - коэффициент настройки на модульный оптимум;

- малая постоянная времени некомпенсируемого апериодического звена;

а_М=1÷4 – коэффициент модульной настройки;

а_М=2 - стандартный коэффициент настройки контура.

Эту передаточную функцию можно записать в форме, соответствующей колебательному звену

, (14.9)

где: - эквивалентная постоянная времени колебательного звена;

- частота недемпфируемых колебаний;

- коэффициент демпфирования колебаний.

Для стандартной настройки ,. определяется соотношением

. (14.10)

Следовательно, с возрастанием коэффициента демпфирования действительная частота колебаний в контуре регулирования уменьшается. При стандартной настройке на МО, когда а_М=2,

, (14.11)

переходный процесс отработки ступенчатого задающего воздействия представлен на рис.14.11. Он описывается уравнением

, (14.12)

Действительная частота колебаний звена второго порядка и имеет следующие показатели качества: время переходного процесса ; время нарастания; время первого максимума; перерегулирование%; число колебаний.

С

Рис.14.11. Переходные функции контура регулирования, настроенного на модульный оптимум

1 – передаточной функции 2-го порядка, а_м=2

2 – эквивалентная по времени τ экспонента

ледовательно, в контуре, настроенном наМО, достигается компромисс между быстродействием и пе-ререгулированием, ко-гда при сравнительно хорошем быстродей-ствии () пе-ререгулирование сос-тавляет менее 5% (%). По дина-мическим показателям этот переходный про-цесс можно считать приемлемым для мно-гих технологических установок. Разомкнутый контур, настроенный наМО, имеет передаточную функцию

. (14.13)

Т

Рис.14.12. ЛАЧХ и ЛФЧХ разомкнутого контура регулирования, настроенного на модульный оптимум

ак как эта пере-даточная функция со-держит одно интегрирующее звено, то кон-тур, настроенный наМО, является однократ-но интегрирующей сис-темой. В соответствии с (14.13) построенными ЛАЧХ и ЛФЧХ разом-кнутого контура, наст-роенного на МО, при-ведены на рис.14.12, где частота среза,- частота сопряжения асимптот, а запас по фазе на частоте среза.

Таким образом, задачей синтеза контура при настройке на МО является выбор регулятора - последовательного коррек-тирующего звена с такой передаточной функцией, чтобы разомкнутый контур имел передаточную функцию (14.13).