
Гайнуллин часть2
.pdff |
′ |
(х, у) = g |
|
′ |
(х, у), |
|
||
1 |
|
1 |
|
|
|
|||
|
′ |
(х, у) = g |
′ |
(х, у), |
|
|||
f |
|
|
|
|
(2) |
|||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
....... |
|
|
|
|
|
|||
|
′ |
(х, у) = g |
|
′ |
|
|
|
|
f |
|
(х, у) |
|
|||||
|
l |
|
|
l |
|
|
|
|
и если при этом каждое решение системы (1) является в то же время решением системы (2), то система (2) называется следствием системы (1). Следствием системы уравнений может быть и одно уравнение. Например, уравнение 3х-2у =3 является следствием системы:
2х + у = 5, |
||
|
х |
− 3у = −2 |
|
||
(как сумма уравнений системы). Вообще следствием системы уравнений может быть система как с меньшим, так и с большим числом уравнений. Так, система
2х + у = 5,
− = −
х 3у 2,3х − 2у = 3
есть следствие системы
2х + у = 5, |
||
|
х |
− 3у = −2. |
|
||
В свою очередь эта система является следствием предыдущей системы. Две системы уравнений называются равносильными, если множества их решений совпадают. Ясно, что две системы равносильны тогда и только
тогда, когда вторая является следствием первой и первая является следствием второй. Отсюда, в частности, следует, что если к системе уравнений добавить еще одно уравнение, являющееся следствием данной системы, то новая система будет равносильна исходной. Если же опустить какое-либо уравнение системы, то оставшееся уравнение (или система уравнений) будет следствием исходной системы.
Если в условии не оговорено, на каком множестве требуется решить систему рациональных уравнений, то предполагается, что решать ее нужно
на множестве комплексных чисел. |
|
|
|
|
|
|||
|
Приведем две теоремы, применяющиеся при решении систем урав- |
|||||||
нений. |
|
|
|
|
|
|
|
|
|
Теорема 1 . |
Если, уравнение f1(х, у) = g1(х, у) равносильно уравнению |
||||||
f ′ |
(х, у) = g ′(х, у), а |
уравнение |
f |
(х, у) = g |
(х, у) |
равносильно уравнению |
||
1 |
1 |
|
2 |
|
|
2 |
|
|
f2′(х, у) = g2′(х, у) , то системы |
|
|
|
|
|
|
||
|
f1(х, у) = g1(х, у), |
|
|
|
′ |
|
′ |
|
|
и |
f1 (х, у) = g1 (х, у), |
||||||
|
|
|
|
′(х, у) = g |
′(х, у) |
|||
|
f2 (х, у) = g2 (х, у) |
|
|
f |
||||
|
|
|
|
|
|
2 |
|
2 |
равносильны.
87
Теорема 2. Если уравнение f (x, y) = g(x, y) является следствием урав-
нений f1(х, у) = g1(х, у) и f2 (х, у) = g2 (х, у) или одного из этих уравнений, то система
или f2 (х, у) = g2 (х, у),f (х, у) = g(х, у)
f1 (х, у) = g1 (х, у),f2 (х, у) = g2 (х, у).
В частности, следствиями системы
|
|
|
|
f |
|
(x, y) = g |
(x, y), |
(3) |
||||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
f2 (x, y) = g2 (x, y) |
|
|||||||||||||
будут такие системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
(х, у) = g |
(х, у), |
|
|
|
|
(4) |
|||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
g1(х, у) ± g2 (х, у), |
||||
f1(х, у) ± f2 (х, у) = |
|
|||||||||||||||||
f |
|
|
(х, у) = |
g |
|
(х, у), |
|
|
|
|
(5) |
|||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
g1(х, у) g2 (х, у), |
|||||
f1(х, у) f2 (х, у) = |
|
|||||||||||||||||
|
|
|
|
f1 (х, у) = g1 (х, у), |
(6) |
|||||||||||||
|
|
|
|
(f |
2 |
(х, у))2 = (g |
2 |
(х, у))2 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если не существует таких пар (х, у), при которых выражения |
f2 (х, у) |
|||||||||||||||||
и g2 (х, у) одновременно обращаются в нуль, то уравнение |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
= |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f2 (х, у) g2 (х, у)
равносильно уравнению f2 (х, у) = g2 (х, у) . Тогда системе (3) равносильна следующая система
f1 (х, у) = g1 (х, у), |
||||
|
|
|
|
|
|
1 |
= |
1 |
. |
|
|
|
||
|
|
|||
f2 (х, у) |
|
g2 (х, у) |
||
|
|
|||
Ее следствием в свою очередь является система:
f1 (х, у) = g1 (х, у), |
|
|
|
|||
|
|
|
|
|
|
|
|
(х, у) |
1 |
= g1 |
(х, у) |
1 |
. |
f1 |
|
|
||||
f2 (х, у) |
|
|||||
|
|
|
|
g2 (х, у) |
||
Таким образом, приходим к следующему выводу: если не суще- |
||||||
ствует таких пар (х, у), при которых оба выражения f2 (х, у) |
и g2 (х, у) од- |
|||||
новременно обращаются в нуль, то система |
|
|||||
f (х, у) = |
g (х, у), |
|
||||
|
1 |
|
1 |
|
(7) |
|
|
f1(х, у) |
= |
|
g1(х, у) |
||
|
|
|
|
|
|
|
f2 (х, у) |
|
g2 (х, у) |
|
|||
|
|
|
||||
|
|
|
|
|||
является следствием системы (3).
88
Если, решая систему, мы преобразовали ее в систему, являющуюся следствием исходной, то найденные решения новой системы, безусловно, подлежат проверке подстановкой в исходную систему. Если же полученная система равносильна исходной, то такая проверка не требуется. Поэтому нам в дальнейшем окажутся полезными следующие замечания.
Замечание 1. Система (4) равносильна системе (3).
Замечание 2. Если не существует таких пар (х, у), при которых обе части уравнения f1(х, у) = g1(х, у) одновременно обращаются в нуль, то система (5) равносильна системе (3).
Замечание 3. Система (6) равносильна системе (3) над полем действительных чисел, если для любых х, у из области определения системы (3) выполняется неравенство f1(х, у) g1(х, у) ≥ 0 .
Замечание 4. Если не существует таких пар (х, у), при которых одновременно обращаются в нуль обе части каждого из уравнений системы (3), то система (7) равносильна системе (3).
Отметим еще один результат, с очевидностью вытекающий из тео-
рем 1 и 2. |
|
|
Теорема3. Если совокупность |
уравнений |
f21(х, у) = g21(х, у) |
f22 (х, у) = g22 (х, у) … f2к (х, у) = g2к (х, у) |
равносильна |
уравнению |
f2 (х, у) = g2 (х, у); (или является его следствием), то совокупность систем
f |
1 |
( х, у ) = g |
1 |
( х, у ), |
|
f |
1 |
( х, у) = g |
1 |
(х, у), |
|
f |
|
(х, у) = g (х, у), |
|
|
|
|
|
|
... |
1 |
1 |
||||||
f21 ( х, у ) = g 21 ( х, у ) |
|
f22 ( х, у) = g 22 ( х, у) |
|
f2к (х, у) = g2к (х, у) |
||||||||||
равносильна системе (3) (или является ее следствием).
В частности, следствием системы
f1(х, у) = g1(х, у),
f21(х, у) f22 (х, у) ... f2к (х, у) = 0
является совокупность систем:
f |
(х, у) = g (х, у), |
|
f |
|
(х, у) = g (х, у), |
f |
|
(х, у) = g |
(х, у), |
1 |
1 |
|
|
1 |
1 |
… |
1 |
1 |
|
f21(х, у) = 0 |
|
f22 (х, у) = 0 |
f2к (х, у) = 0. |
||||||
Замечание5. Аналогичные результаты справедливы для систем уравнений с тремя, четырьмя т. д. переменными.
Основные методы решения систем
1.Метод линейного преобразования системы (или метод алгебраического сложения).
2.Метод подстановки.
3.Метод замены переменных.
Метод линейного преобразования системы основан на следующей теореме.
89
|
Теорема 4. Если |
|
а2 |
|
f1(х, у) = 0, и |
||||
|
= |
а1 |
≠ 0 , то системы |
||||||
|
|
|
|
|
|
b1 |
b2 |
|
f2 (х, у) = 0 |
а f |
(х, у) + а |
|
f |
(х, у) = 0, |
|
|
|
|
|
1 1 |
|
2 |
2 |
|
|
|
|
|
|
b1 f1(х, у) + b2 f2 (х, у) = 0 |
|
|
|
|
|
||||
равносильны.
В частности, если а1 =1,а2 = 0,b1 =1,b2 = ±1, то получим систему
f1(х, у) = 0,
f1(х, у) ± f2 (х, у) = 0
равносильную исходной.
Естественным образом эта теорема распространяется на случай большего числа уравнений. Например, для трех уравнений с тремя неизвестными имеет место следующая теорема.
|
а1 а2 а3 |
|
||
Теорема 4’. Если = |
b1 |
b2 |
b3 |
≠ 0 , |
|
с1 |
с2 |
с3 |
|
то системы
f |
|
( |
х, |
у, z) = 0, |
а f |
+ |
а |
|
|
f |
|
+ а f |
|
= 0, |
|||||
1 |
|
|
|
|
1 1 |
|
|
2 |
|
|
2 |
|
3 |
|
3 |
|
|
||
f2 (х, у, z) = 0, и |
b1 f1 + b2 f2 + b3 f3 = 0, |
равносильны. |
|||||||||||||||||
f |
3 |
(х, у, z) = 0 |
с f |
+ с f |
2 |
+ с f |
3 |
= 0 |
|
||||||||||
|
|
|
|
|
1 1 |
|
2 |
|
|
|
3 |
|
|
||||||
Метод подстановки основан на следующей теореме. |
|||||||||||||||||||
Теорема 5. Системы уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
х = F(у), |
|
|
|
х = F(у), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (х, у) = g(х, у) |
f (F(у), у) = g(F(у), у) |
|
|
|
|
||||||||||||||
равносильны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так, равносильными будут следующие системы |
|||||||||||||||||||
|
х = 2у − 5, |
и |
х = 2у − 5, |
|
|
||||||||||||||
|
|
х2 |
+ у2 |
= 2х + |
|
(2у |
− 5)2 + у2 |
= 2(2у − 5) + у. |
|||||||||||
|
|
у |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следствие. |
Если |
уравнение |
|
ϕ(х, у) = 0 равносильно уравнению |
|||||||||||||||
х = F(у) (или уравнению у = F(х) ), то системе |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
ϕ (х, у) = 0, |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (х, у) = g(х, у) |
|
||||||||||||
равносильна система |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
х = F(у), |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
f (F(у), у) = g(F(у), у) |
||||||||||||||
или системе |
|
у = F(х), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
f (х, F(х)) = g(х, F(х)). |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
у2 + х = 2(х − 5), |
|||||||||||
Например, системе уравнений |
у |
+ |
х |
= х |
2 |
+ у |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
х |
|
|
|
у |
|
|
|
|
|
|||
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
равносильна следующая система
|
х |
= у2 +10, |
|
|
|
|||
|
|
|
|
|
у2 |
+10 |
|
|
|
|
|
у |
+ |
= (у2 |
+10)2 + у2. |
||
|
|
|
|
|
|
|||
|
2 |
+10 |
|
у |
||||
у |
|
|
|
|
|
|||
В случае системы трех уравнений с тремя переменными соответствующая теорема формулируется следующим образом.
Теорема 5’. Системе уравнений
|
|
|
f |
|
(х, у, z) = g (х, у, z), |
|
|
|
||||
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
f |
2 (х, у, z) = g2 (х, у, z), |
|
|
||||||
|
|
|
|
= F(х, у) |
|
|
|
|
|
|
||
|
|
|
z |
|
|
|
|
|
|
|||
равносильна следующая система |
|
|
|
|
|
|
||||||
f (х, у, F(х, у)) = g |
(х, у, F(х, у)), |
|
|
|||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
f |
2 (х, у, F(х, у)) = g2 (х, у, F(х, у)), |
|
|
|||||||||
|
= F(х, у). |
|
|
|
|
|
|
|
||||
z |
|
|
|
|
|
|
|
|||||
Метод замены переменных состоит в следующем. |
||||||||||||
Если F1(х, у) = f1[ϕ1(х, у),ϕ2 (х, у)] |
и F2 (х, у) = |
f2[ϕ1(х, у),ϕ2 (х, у)], |
||||||||||
то систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
(х, у) = 0, |
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
F2 (х, у) = 0 |
|
|
|
||||
с помощью новых переменных ϕ1(х, у) = u,ϕ2 (х, у) = v |
можно записать в |
|||||||||||
|
|
|
|
|
f |
(u,v) = 0, |
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
f2 (u,v) = 0. |
|
|
|
||||
Пусть (u1,v1);(u2 ,v2 );...;(uп ,vп ); - решения последней системы. Тогда за- |
||||||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
дача сводится к решению следующей совокупности систем |
|
|||||||||||
ϕ (х, у) = u |
, |
|
ϕ (х, у) = u |
|
, |
... |
ϕ (х, у) = u |
, |
||||
1 |
1 |
|
1 |
|
2 |
|
1 |
п |
|
|||
ϕ2 (х, у) = v1 |
|
|
ϕ2 (х, у) = v2 |
|
|
ϕ2 (х, у) = vп. |
||||||
Решения этой совокупности будут одновременно и решениями сис-
темы
F1(х, у) = 0,
F2 (х, у) = 0.
Пример1. Решим систему
|
ху − 6 = |
у3 |
|
||
|
|
|
, |
|
|
|
|
|
|||
|
|
х |
(8) |
||
|
|
|
х3 |
||
|
ху + 24 = |
|
|||
|
|
||||
|
|
|
у |
|
|
|
|
|
|
||
на множестве действительных чисел.
Решение. Перемножив уравнения системы, получим систему
91
|
ху − 6 |
= |
у3 |
|
|||
|
|
, |
|
|
|||
|
|
||||||
|
|
|
х |
(9) |
|||
|
|
|
|
|
у3 х3 |
||
(ху + 24)(ху − 6)= |
, |
||||||
|
|||||||
|
|
|
|
|
ху |
|
|
|
|
|
|
|
|
||
являющуюся следствием исходной. Второе уравнение системы (9) путем несложных преобразований сводится к уравнению ху=8 — следствию второго уравнения системы (9). Тогда система
|
ху − 6 = |
у3 |
|
|
|
|
, |
(10) |
|
|
||||
|
|
х |
|
|
|
ху = 8 |
|
|
|
|
|
|
|
будет следствием системы (9).
Вычтем теперь первое уравнение системы (10) из второго. Получим систему
ху = 8, |
|
|
|
|
|
у3 |
(11) |
|
= 8 − |
||
6 |
|
|
|
|
|
||
|
|
х |
|
и далее Система (11) —следствие системы (10).
Перемножим уравнения системы (11). Получим систему
ху |
= 8, |
|
|
|
(12) |
|
у4 |
= 16, |
которая будет следствием системы (11). Из второго уравнения системы (12) находим у1 = 2, у2 = -2 (ограничиваемся действительными корнями), а из первого уравнения, соответственно, х1 = 4, х2 = -4.
Итак, система (12) имеет следующие решения: (4; 2) и (-4; -2). Проверка. Поскольку система (12) является в конечном счете следст-
вием системы (8), то найденные решения системы подлежат проверке, которую можно выполнить с помощью подстановки найденных решений системы (12) в систему (8). Эта проверка показывает, что оба решения системы (12) являются и решениями системы (8). Таким образом, решениями системы (8) являются пары: (4; 2) и (-4; -2).
Пример 2. Решить систему:
ху + хz = −4,
уz + yx = −1,
zx + zy = −9.
Решение. Сложив все три уравнения системы, получим: ху+уz+хz=- 7. Присоединив это уравнение к уравнениям заданной системы, получим равносильную систему:
92
ху + yz + xz = −7,
|
|
= −4, |
ху + хz |
||
|
уz + yx = −1, |
|
|
||
|
|
= −9. |
zx + zy |
||
Заменим второе уравнение этой системы разностью первых двух |
||
уравнений, третье уравнение — разностью первого и третьего, а четвертое
— разностью первого и четвертого, кроме того, опустим первое уравнение. Получим систему
уz = −3, |
|
|
|
хz = −6, |
|
|
ху = 2, |
|
|
являющуюся следствием предыдущей. Перемножив все три уравнения, получим: х2у2z 2 = 36. Приписав это уравнение к уравнениям предыдущей системы, придем к равносильной системе
х2 |
у2 z2 |
= |
36, |
|
|
|
= −3, |
|
|
yz |
|
|
||
|
|
= −6, |
|
|
хz |
|
|
||
|
|
= 2, |
|
|
xу |
|
|
|
|
которой в свою очередь равносильна следующая совокупность си- |
||||
стем |
|
|
|
|
хуz = 6, |
|
|
хуz = −6, |
|
|
|
|
|
|
yz = −3, |
|
yz = −3, |
||
|
|
|
|
|
хz = −6, |
|
|
|
хz = −6, |
|
|
|
|
|
xу = 2 |
|
|
xу = 2. |
|
Решим первую систему этой совокупности. Разделив последовательно первое уравнение системы на второе, третье, четвертое, получим
х = −2,у = −1,
z = 3.
Аналогично из второй системы находим
х = 2,
у = 1,
z = −3.
Итак, совокупность систем имеет следующие решения: (-2; -1; 3) и (2; 1; -3).
Будут ли эти решения решениями исходной системы? Пока мы этого утверждать не можем, так как полученная выше совокупность систем является, в конечном счете, следствием исходной системы. Значит, обязательна проверка найденных решений.
93

Проверка. Проверку несложно осуществить с помощью подстановки найденных решений совокупности систем в исходную систему. Эта подстановка показывает, что обе тройки (-2; -1; 3) и (2; 1; -3) являются реше-
ниями исходной системы.
Пример 3. Решим систему уравнений
х + у + z = 2,2х + 3у + z = 1,
( ) ( )
х2 + у + 2 2 + z −1 2 = 9.
Решение. Применим метод подстановки. Имеем
х = 2 − у − z,
( − − )+ + =
2 2 у z 3у z 1,
( − − )2 + ( + )2 + ( − )2 =
2 у z у 2 z 1 9
и далее
х = 2 − у − z,
у − z = −3,
2 + 2 + − =
у z уz 3z 0.
Последние два уравнения полученной системы в свою очередь образуют систему двух уравнений с двумя переменными. Решим эту систему методом подстановки. Имеем
у = z − 3, |
|
|
(z − 3)2 |
+ z2 |
+ (z − 3)z − 3z = 0, |
|
|
|
т.е.
у = z − 3,
z2 − 4z + 3 = 0.
Из последнего уравнения находим: z1 = 1, z2 = 3. Из уравнения у = z - 3 получаем соответственно: у1=-2, у2 = 0, а из уравнения х = 2 - у –z находим х1=3 и x2=-1.
Итак, получили следующие решения: (3; -2; 1) и (-1; 0; 3). Пример 4. Решить дизъюнкцию уравнений:

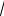 х +1 = х −1 −
х +1 = х −1 −
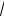 х +1 = х −1.
х +1 = х −1.
Решение.
1) |
|
|
|
х −1≥ 0, |
х ≥ 1, |
|
|
х ≥ 1, |
|
х ≥ 1, |
х = 3. |
|||||
|
|
|
||||||||||||||
х +1 = х −1 |
х +1 = (х −1)2. |
|
х(х − 3) = 0. |
|
х = 0. |
|
х = 3. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
х −1≤ 0, |
|
х ≤ 1, |
|
|
х ≤ 1, |
|
|
х ≤ 1, |
|
||
2) − |
|
х +1 = х −1 |
|
|
|
|
х = 0. |
|||||||||
|
|
|
= |
|
|
|
х = |
|
||||||||
|
|
|
|
|
х +1 = (х −1) |
2. |
х(х − 3) |
0. |
х = 0. |
|
|
3. |
|
|||
Ответ. {0; 3}.
Пример 5. Решить дизъюнкцию уравнений:
3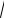 х2 + 6х = х −3
х2 + 6х = х −3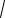 − х2 − 6х = х.
− х2 − 6х = х.
94

Решение.
1) 3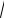 x2 + 6x = x x2 + 6x = x3 x(x2 − x − 6) = 0 x = −2 х = 0 х = 3.
x2 + 6x = x x2 + 6x = x3 x(x2 − x − 6) = 0 x = −2 х = 0 х = 3.
2) − 3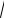 x2 − 6x = x 3
x2 − 6x = x 3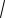 x2 − 6x = −x x(x2 + x + 6) = 0 ; x = 0 .
x2 − 6x = −x x(x2 + x + 6) = 0 ; x = 0 .
Ответ. {-2, 0, 3}.
Упражнения.
Решить систему уравнений (481-491):
|
|
|
х |
|
+ 3у = 7, |
|
|
|||||||
481. |
|
|
|
|
|
|
|
у −1 |
|
= 3 |
|
|||
|
|
|
|
|
|
|
|
|||||||
|
2х + 2 |
|
над R. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
+ 2 |
|
y |
|
= 3, |
|
|
|||
|
|
|
|
|
|
|
||||||||
482. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2(x −1)2 + (y − 2)2 = 1 над R. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
483. |
|
х2 + у |
= 20, |
|
|
|||||||||
|
х + у2 |
= 20 |
|
|
||||||||||
|
|
над |
С. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ху + уz = 8, |
|
|
|||||||||||
484. |
уz + zx = 9, |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
над R. |
|
|
zx + xy = 5 |
|||||||||||||
ху + хz = х2 + 2,
487.ху + уz = у2 + 3,
xz + уz = z2 + 4 над R.
0 < (x − 2)2 < 25, |
|||
488. |
х2 |
+ 4х + 4 |
≥ 0 над R. |
|
|
|
|
|
х +1 |
||
|
|
|
|
х + у + z = 0, |
|||
489. 3х2 + 3z2 − 5хуz = 0,
2х3 + 2у3 + 3хуz = 0 над R.
|
х + у + z = |
13 |
|
|
|||||||
|
, |
|
|||||||||
|
|
||||||||||
490. |
|
|
|
3 |
|
|
|||||
хуz = 1, |
|||||||||||
|
1 |
|
1 |
|
1 |
|
|
13 |
|
||
|
+ |
+ |
= |
над R. |
|||||||
|
|
|
|
||||||||
|
|
|
у |
|
z 3 |
||||||
х |
|
|
|||||||||
|
х + у + z = 2, |
|
|
х2 + уz = у + z, |
|||||||||
485. |
|
х |
2 |
+ у |
2 |
+ z |
2 |
= 6, |
491. |
|
у |
2 |
+ zх = z + x, |
|
|
|
|
|
|
||||||||
|
x |
3 |
+ y3 + z3 |
= 8 над С. |
|
z2 |
+ ху = х + у над R. |
||||||
х + у + z = 3,
486.х2 + у2 + z2 = 5,
x4 + y4 + z4 = 17 над С.
Решить дизъюнкцию уравнений над R (492-500):
|
|
х2 − 5х + 6 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
492. |
|
496. |
|
|
|
|
х + 3 = 3− |
|
|
х х + 3 = 3+ х. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
х2 − х − 2 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х − у = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
493. |
|
497. |
|
|
− х |
|
х2 |
= −х − |
|
|
− х |
|
х2 = −х. |
|||||||||||||||||||||||||||||
|
х + у = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
х − у = 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
х |
2 |
+ 4 − |
|
х |
2 |
− 4 |
= х |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2, |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
494. |
ху = 1, |
|
|
|
|
498. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
2 |
+ 4 + |
|
|
х |
2 |
− 4 = х 2. |
|||||||||||||||||||||
|
log |
|
x |
= −1. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
2 |
|
|
− |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
х2 + 5х +1 = 2 |
х −1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
495. |
|
|
|
|
|
|
|
|
|
|
499. |
3 |
2х − х2 = х −3 |
х2 − 2х = х. |
||||||||||||||||||||||||||||
|
|
|
|
х |
|
+ 5х +1 = 2х −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
95 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
3 |
х2 + 4х − 5 = х −1, |
|
||||
500. |
|
|
|
|
|
|
|
|
|
3 |
− х |
2 |
− 4х + 5 |
= х |
−1. |
|
− |
|
|
||||
Решить системы уравнений, используя метод подстановки (501-506):
501. |
|
х + у = 9, |
504. |
|
|
ху = 8. |
|
502. |
|
х2 + у2 = 25, |
505. |
|
у − х = −1. |
||
|
|
|
|
503. |
|
х2 − ху − 3у = 5, |
506. |
|
у − 2х = 0. |
||
|
|
|
х2 + ху − 3у2 = −3,
3у − 2х = 2.
у2 − 2х2 = −14,
ху = 6.
х2 − у2 = 3,
4 + 4 =
х у 17.
Решить однородные системы уравнений (507-514):
507. |
2х2 |
+ ху − 6у2 = 0, |
511. |
|
|
||
|
х2 − 4ху + 3у2 = −3. |
|
|
|
|
|
|
508. |
8х2 |
+ 2ху − 3у2 = 0, |
512. |
|
|
||
|
4х2 |
− 3ху − 9у2 = −38. |
|
|
|
|
|
509. |
4х2 |
− 3ху − у2 = 0, |
513. |
|
|
||
|
32х2 − 36ху + 9у2 = |
6. |
|
|
|
|
|
510. |
2х2 |
− 3ху + у2 = 6, |
514. |
|
− 2ху − 2у2 = 3. |
||
|
3х2 |
|
|
|
|
|
|
|
х2 |
− у2 = 5, |
|
|
|
|
х2 |
− ху + у2 = 7. |
|
||
|
|
|
2х2 |
+ 3у2 − 4ху = 3, |
|||
|
|
|
|
|
|
|
|
− у2 = 7. |
|
2х2 |
|
|||
|
|
|
|
|
|
х2 |
− 3ху + у2 = −5, |
||
|
|
|
|
|
|
|
|
− ху + 2у2 |
= 20. |
2х2 |
||||
|
|
|
|
|
5х2 |
+ 2ху + у2 |
= 20, |
||
|
|
|
|
|
|
х2 |
+ 2ху + 2у2 |
= 25. |
|
|
||||
|
|
|
|
|
Решить системы уравнений, используя метод замены переменных (515522):
|
|
|
|
3 |
|
|
|
|
+ |
|
|
|
1 |
|
= |
|
2 |
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2х − у |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
520. |
||||||||
515. |
2х + у |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
= |
|
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2х − у |
|
|
5 |
|
|
|
|
|
|||||
|
2х + у |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
11 |
521. |
|||
|
|
х |
2 |
− ху |
|
− |
|
2 |
− ху |
|
= |
|
|
|
, |
|||||||||||
|
|
|
|
|
||||||||||||||||||||||
516. |
|
|
|
|
|
|
у |
|
|
|
|
|
12 |
|
|
|||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
+ |
|
|
|
|
= − |
. |
||||||||||||
|
|
х |
2 |
− ху |
у |
2 |
− ху |
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
522. |
|||||||||||||
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4ху − |
|
|
|
|
= 30, |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
517. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3ху + 2 |
= 28. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х + у |
+ |
|
х − у |
= |
10 |
, |
|
|
|
|
|
||||||||||||||
518. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
х − у |
|
х + у |
3 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
+ у |
2 |
= 27. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2х |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
519. |
|
х−1 + 2у−1 =14, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
х−2 + у−2 = 41. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
96 |
|
х |
+ |
у |
= |
|
5 |
|
, |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
у |
х |
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
х |
2 |
− 2 |
у |
2 |
= 2. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
х − |
у |
+ |
|
|
х + у |
= |
26 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||
|
|
|
х + |
|
|
|
|
|
|
|
− у |
|
|||||||||||
|
|
|
|
у |
|
|
|
|
|
х |
|
|
|
5 |
|
||||||||
|
ху − 6х − 6у = 6. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3х − 2 |
+ |
|
|
|
|
у − |
1 |
|
= 2, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
у −1 |
|
|
|
|
|
3х − 2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
х + у = 11. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
