
Гайнуллин часть2
.pdf
x = πk, x |
2 |
= ± π |
+ πn, k,n Z . |
||
1 |
3 |
|
|
|
|
|
|
|
|
|
|
Так как в процессе решения выполнялись только равносильные пре- |
|||||
образования, то совокупность семейств x |
= πk, x |
2 |
= ± π + πn, k,n Z . |
||
|
|
1 |
|
3 |
|
|
|
|
|
|
|
является общим решением уравнения (2). Впрочем, эти семейства |
|||||
можно объединить в одно: x = π m,т Ζ |
(для того чтобы в этом убедить- |
||||
3 |
|
|
|
|
|
ся, рекомендуем читателю изобразить х1 и х2 точками числовой окружно-
сти). Итак, x = π m, m Z - решение уравнения (2).
3
Пример 3. Решим уравнение
sin х + 2sin 2х = 3+ sin3х. |
(4) |
Решение. Преобразуем уравнение (4) к виду |
(sin х − sin 3х) + 2sin 2х = 3, |
и далее 2sin хcos2х − 2sin 2х + 3 = 0.
Дополним имеющиеся удвоенные произведения 2sin хcos2х и 2sin 2х до полных квадратов:
(sin2 х + 2sin хcos 2х + cos2 2х) + (sin2 2х − 2sin 2х +1) + 3 = sin2 х + cos2 2х + sin2 2х +1,
т.е. (sin х + cos 2х)2 + (sin 2х −1)2 + 3 = sin2 2х +1, |
|
(sin х + cos 2х)2 + (sin 2х −1)2 + cos2 х = 0 . |
(4а) |
Но сумма квадратов равна нулю тогда и только тогда, когда каждое слагаемое равно нулю. Поэтому уравнение (4а ) равносильно следующей системе уравнений:
sin х + cos2х = 0, |
|
|
|
|
= 0, |
|
(4б) |
sin 2х −1 |
. |
||
cos х = 0.
Решив третье (самое простое) уравнение системы (4б), получаем:
x = π + πn, n Z .
2
Подставим эти значения во второе уравнение системы. В левой части
указанного уравнения: sin 2(π +πп) −1 = sin(π + 2πп) −1= −1≠ 0 , т.е. значения
2
x = π + πn, n Z не удовлетворяют второму уравнению системы (4б). Но то-
2
гда система (4б) несовместна; таким образом, уравнение (4) не имеет ре-
шений.
Пример 4. Решим уравнение
− 3 − cos2 x + 3sin5x = 1− sin x. |
(5) |
Решение. Возведя обе части уравнения (5) в квадрат и выполнив по- |
|
следующее приведение подобных членов, получим: |
|
2sin х + 3sin5х = 5 . |
(5а) |
117
Так как sin х ≤1,sin5х ≤1, то уравнению (5а) удовлетворяют те и только те значения х , при которых одновременно sin х =1 и sin5х =1. Иными словами, уравнение равносильно следующей системе уравнений:
sin х = 1, |
(5б) |
|
|
sin 5х = 1. |
|
Решим эту систему. Из уравнения sin х =1 |
находим: х = π + πп,n Z. |
|
2 |
Подставив эти значения х в левую часть второго уравнения системы (5б),
получаем: sin 5(π + 2πп) = sin(5π +10πп) = sin π = 1, n Z.
2 |
2 |
2 |
Таким образом, |
х = π + πп,n Z.- решение системы (5б), а значит, и |
|
|
2 |
|
уравнения (5а).
Но при возведении обеих частей уравнения (5) в квадрат могли появиться посторонние решения, поэтому необходимо сделать проверку. В данном случае ее нетрудно осуществить подстановкой найденных значений в исходное уравнение. Имеем в левой части уравнения (5):
− 3 − cos2 (π + 2πn) + 3sin 5(π + 2πn) = 0, n Z
22
ив правой части: 1− sin(π + 2πn) = 0.
2
Значит, x = π + πn, n Z - решение уравнения (5).
2
Решить уравнения (614-635):
614.sin х = − 1 . 2 2
615.cos(2х +1)= − 
 3 .
3 .
2
616.tg х = −
 3. 3
3. 3
617.ctg3х = −  3 .
3 .
3
618. cos(3х − 2)= − 1 . 2
619.4cos3 х + 3cos(π − х)= 0.
620.2sin хctgx +1= cos(− х).
621. |
|
sin x |
= −2 − ctg(х +π ). |
|
|
||
|
1+ cos x |
||
622. |
4sin х + 5cos х = 3. |
||
623. |
7sin х −5cos х = 5. |
||
Упражнения
624. sin х − cos х =  2 . 2
2 . 2
625.cos3xtgх = 0.
626.1+ cos(π − х) = sin х .
|
|
|
|
sin x |
2 |
|
|
|
|
|
|||||||||||
627. tgх +1= 2sin x + |
1 |
|
|
. |
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|||||||
628. sin 2х + 3sin х = tg |
х |
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
629. |
2cos2х −8cos x + 7 = |
|
1 |
. |
|||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
||
630. |
|
7 |
cos |
х |
|
= cos3 |
x |
|
+ sin |
х |
. |
||||||||||
|
|
|
|
|
|
||||||||||||||||
|
4 |
|
4 |
|
|
4 |
|
|
|
|
|
2 |
|
|
|||||||
631. |
|
tg2х |
+ |
tgх |
= |
5 |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
tgx |
|
|
|
|
tg2x |
2 |
|
|
|
|
|
|
|
|
|
||||
632.sin3 х + cos3 х = 1.
633.sin xtgх = 9 .
−cos x 41
118

634. ctgx − 2sin 2x = 1. |
635.sin4 х + cos4 х = |
5 |
. |
|
|
||
|
8 |
|
|
Решить уравнения с параметрами (636-647): |
|||
636. аsin x + bcos х = аsin 2x − bcos2х. |
642. sin4 х + cos4 х + sin 2х = а. |
||
637. sin2 х + аsin2 х = 1 .
22
638.(3− а)tg2 x − 2tgx − (а + 3)= 0.
639.4cos2 х + 2cos х + а −1= 0.
640.2sin2 х − 2cos х + а − 2 = 0,0 < а < 4.
641. sin |
2 |
|
π |
|
π |
+ 2а −1= 0. |
|
х − |
|
− 2аsin х − |
|
||
|
|
|
4 |
|
4 |
|
643. sin(х + а)+ sin х = cos а . 2
644.а(cos х + sin х)2 = bsin 2х.
645.аsin x + b = acos x + b ,а ≠ 0,b ≠ 0.
+a bsin x + abcos x
646. а(cos х −sin х)= b(1− sin 2х).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х+а−1 |
|
|
|
π |
2 |
|
|
|
|
|
||||
х |
+2а−3 |
|
1 |
|
|
|
|||||
647. cos |
|
|
|
|
= |
|
|
|
. |
||
|
|
|
|
π |
|||||||
|
5 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
cos |
5 |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
§4. Решение тригонометрических неравенств
Решение тригонометрических неравенств сводится, как правило, к решению простейших тригонометрических неравенств, т. е. неравенств вида sin x > a,cos x < a и т. д., а также к решению совокупностей, систем или совокупностей систем простейших тригонометрических неравенств. Для решения простейших тригонометрических неравенств во многих случаях удобно пользоваться числовой окружностью, на которой множество значений переменной, удовлетворяющих заданному простейшему неравенству, изображается в виде одной или нескольких дуг. Напомним, как определяется числовая окружность.
Пусть R — числовая прямая, а Σ — окружность единичного радиуса (точнее, Σ—множество точек окружности). Определим отображение Ф множества R на множество Σ следующим образом:
1)полагаем Ф (0) = Θ0, где Θ0 — правый конец горизонтального диаметра окружности Σ (рис. 1);
2)если x R и х > 0, то, отправляясь из точки Θ0, будем двигаться по окружности Σ в положительном направлении (в направлении против часовой стрелки) до тех пор, пока не будет пройден путь длины х; конец этого пути — точку t — и поставим в соответствие числу x:t=Ф(х);
119

3) если x R и х< 0, то, отправляясь из точки Θ0, будем двигаться по окружности в отрицательном направлении (в направлении по часовой стрелке) до тех пор, пока не будет пройден путь длины |х|; конец этого пути — точку t — и поставим в соответствие числу x:t=Ф(х).
Если задано указанное отображение Ф множества R на множество Σ, то единичную окружность Σ будем называть числовой окружностью.
Аналогично тому, как с помощью неравенства задаются промежутки на числовой оси, можно записывать и множество точек, принадлежащих той или иной дуге числовой окружности.
Условимся символом М1М2 обозначать дугу, для которой точка М1
— начальная точка (в обозначении дуги она записывается первой), М2 — конечная точка пути, описываемого текущей точкой по окружности Σ в положительном направлении.
Так, пусть с помощью неравенства требуется записать следующие замкнутые дуги числовой окружности Σ (рис. 2): 1) Θ0Θ1 ;2) Θ1Θ3 ; 3)
Θ Θ |
0 |
; 4) |
Θ Θ ; 5) |
Θ |
М ; 6) МΘ |
0 |
; 7) |
Θ |
М ; |
|
1 |
|
2 |
1 |
0 |
|
|
3 |
|
||
где точка М — середина дуги Θ1Θ2.
1)Точка Θ0 соответствует числу 0, точка Θ1 соответствует числу π ,
2
поэтому текущая точка дуги Θ0Θ1 соответствует числу х0 такому, что
0 ≤ х ≤ π .
2
Учитывая, однако, что если точка окружности соответствует числу х, то она соответствует и всем числам вида х + 2πк , k Z (к целое), получаем, что точки дуги Θ0Θ1 соответствуют числам х, удовлетворяющим следую-
щей системе неравенств:
0 + 2πk ≤ х ≤ π + 2πk, или 2πk ≤ х ≤ π + 2πk, k Z. 2 2
Это аналитическая запись дуги Θ0Θ1.
2)Для дуги Θ1Θ3 получаем:
π+ 2πk ≤ х ≤ 3π + 2πk, k Z .
22
3)Как было отмечено выше, в этом случае под записью Θ1Θ0 пони-
мается дуга Θ1Θ2Θ3Θ0. При первом обходе окружности точка Θ1 соответст-
120
вует числу π , а точка Θ0 – числу 2π (но не числу 0, так как обход окруж-
2
ности от Θ1 к Θ0 идет в положительном направлении), значит, аналитиче-
ски Θ Θ |
0 |
можно записать следующим образом: |
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π + 2πk ≤ х ≤ 2π + 2πk , k Z . |
||
|
|
2 |
|
|
||||
4) Дугу Θ2Θ1 можно записать двумя (эквивалентными) способами: |
||||||||
a)− π + 2πk ≤ х ≤ π + 2πk , k Z ; |
||||||||
|
|
2 |
|
|
|
|
||
б)π + 2πn ≤ х ≤ |
5π |
+ 2πп, k Z . |
||||||
|
||||||||
|
|
2 |
|
|
|
|
|
|
5) |
|
Дуга Θ0М: 2πk ≤ х ≤ |
3π |
+ 2πk, k Z . |
||||
|
|
|||||||
|
|
2 |
|
|||||
6) |
|
Дуга МΘ0: |
3π |
+ 2πk ≤ х ≤ 2π + 2πk, k Z . |
||||
|
|
|||||||
|
|
4 |
|
|
|
|||
7) Дуга Θ3М: − π + 2πk ≤ х ≤ 3π + 2πk, k Z .
24
Замечание. Записывая дугу в виде
α + 2πk ≤ х ≤ β + 2πk, k Z . (*)
необходимо следить за тем, чтобы выполнялось неравенство α < β , иначе система неравенств (*) окажется противоречивой.
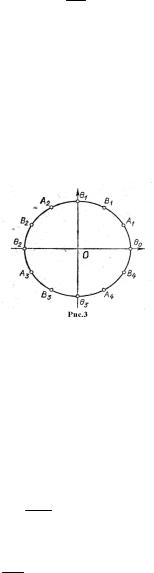
Пусть теперь каждая четверть числовой окружности разбита на три равные части (рис. 3) и требуется найти аналитические записи следующих дуг: 1) В1В2 ; 2) Θ1В4 ; 3) В3 А1 ; 4) А2В1 ; 5) А4Θ2 ; 6) А3В2 .
1) Рассмотрим дугу В1В2 .Так как каждая из дуг Θ0А1, А1В1, В1Θ1, Θ1А2,
…,В4Θ0 |
имеет длину π , то при первом положительном обходе окружности |
|||||
|
6 |
|
|
|
|
|
точка В1 |
соответствует числу π , точка В2 |
- числу |
5π |
. Следовательно, ана- |
||
|
||||||
|
|
3 |
|
6 |
|
|
литическая запись дуги В1В2 будет такой: |
|
|
|
|||
|
π + 2πk < х < |
5π |
+ 2πk , k Z ; |
|||
|
|
|||||
|
3 |
6 |
|
|
|
|
2) дуги Θ1А4: π + 2πk < х < 11π + 2πk, k Z ;
26
3)для дуги В3А1 можно дать две аналитические записи:
− 2π + 2πk < х < π + 2πk, k Z ;
3 6
121
или
4π + 2πn < х < 13π + 2πn, k Z .
36
Еще раз обращаем внимание читателя на необходимость контроля при записи концов дуг. Так, при первом обходе числовой окружности точ-
ка В3 соответствует числу 4π ; продолжая движение в направлении от точ-
3
ки В3 к А1 , мы при переходе через точку Θ0 начинаем обходить окружность
второй раз, т. е. точка А1 соответствует теперь числу 13π . Отсюда и полу-
6
чается система неравенств для дуги В3А1:
4π + 2πk < х < 13π + 2πk, k Z .
36
4) |
А В : − |
4π |
|
+ 2πk < x < π + 2πk (или |
2π |
+ 2πk < х < |
7π |
+ 2πk ), k Z ; |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
2 |
1 |
3 |
3 |
|
3 |
|
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
5) |
А Θ |
|
: − π |
|
+ 2πk < х < π + 2πk (или |
|
5π |
|
+ 2πk < х < 3π + 2πk ), k Z ; |
||||||||||||||
2 |
|
|
|
||||||||||||||||||||
|
4 |
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6) |
А В :− |
5π |
|
+ 2πk < х < |
5π |
+ 2πk (или |
7π |
|
+ 2πk < х < |
17π |
+ 2πk ), k Z ; |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
3 |
2 |
|
6 |
|
6 |
|
6 |
|
6 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пример 1. Решим неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin x > |
1 |
. |
(1) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
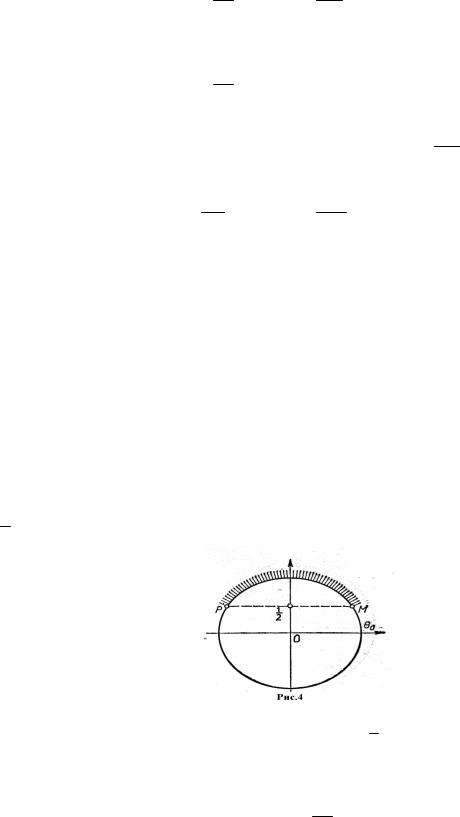
Решение. По определению, sin x — это ордината точки t числовой окружности Σ, соответствующей числу x R при отображении Ф. Отметим на числовой окружности Σ (радиуса 1)точки, имеющие ординату, равную
1 (точки М и Р на рис. 4).
2
Тогда точки, ордината которых больше 1 , заполняют открытую дугу
2
МР. Эту дугу естественно назвать геометрическим решением неравенства
(1). Cоставим аналитическую запись дуги МР:
π + 2πk < х < 5π + 2πk , k Z .
66
Это и есть общее решение неравенства (1). Пример 2. Решим неравенство
122
cos x < |
1 |
(2) |
|
||
3 |
|
|
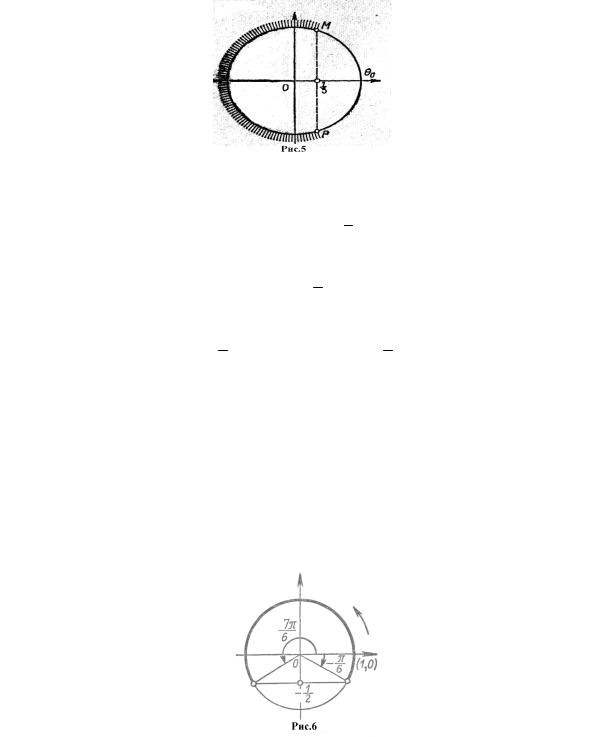
Решение. По определению, cos x - это абсцисса точки t Σ , соответствующей числу x R при отображении Ф. Отметим на числовой окружно-
сти Σ точки, имеющие абсциссу, равную 1 (точки М и Р на рис.5). Тогда
3
геометрическим решением неравенства (2) будет открытая дуга МР (точки
этой дуги имеют абсциссу, меньшую 1 ). Составим аналитическую запись
3
дуги МР:
arccos 1 + 2πk < x < 2π − arccos 1 + 2πk, k Z .
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
Пример 3. Решить неравенство |
|
|
|
|
|
|
|
|
|
|||
|
|
2cos2 х − 7sin x < 5. |
|
|
|
|
|
(1) |
||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
(1) 2 − 2sin2 х − 7sin x < 5 2sin2 х + 7sin x + 3 |
> 0 |
2 sin x + |
1 |
(sin x + 3)> 0 |
||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
|
1 |
(*) |
1 (**) |
π |
+ 2πn < x < |
7 |
π + 2πп, k Z . |
|||||
sin x < −3 sin x > |
|
sin x > − |
|
− |
|
|
||||||
2 |
2 |
6 |
6 |
|||||||||
|
|
|
|
|
|
|
|
|||||
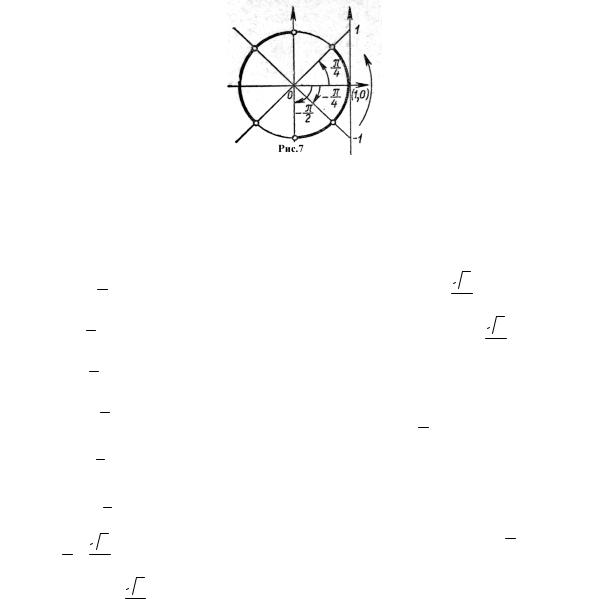
(*): так как | sin x | ≤ 1 при − ∞ < х < ∞. (**): См. рис.6.
Ответ. |
х | − π |
+ πп < х < |
7π |
+ πп, n Z . |
|
||||
|
6 |
6 |
|
|
Пример 4. Решить неравенство
tg3x + tg2x − tgx −1< 0. |
(1) |
Решение.
(1) tg2 x(tgx +1)− (tgx + 1)< 0 (tgx + 1)(tg2 x −1)< 0 (tgx + 1)2 (tgx −1)< 0
123
|
|
х |
≠ − |
π |
+ πk, k Z, |
|
|||
tgx ≠ −1, |
|
4 |
|
||||||
|
|
|
π |
|
|
|
π |
|
|
tgx < 1 |
(*) |
|
+ πп < х < |
+ πп, n Z |
|
||||
|
− |
|
|
|
|||||
|
|
|
2 |
|
|
|
4 |
|
|
− π + πп < х < − π + πп − π + πп < х < π + πп, n Z.
2 |
4 |
4 |
4 |
(*): См. рис.7.
|
π |
+ πп < х < − |
π |
|
|
π |
+ πп < х < |
π |
|
Ответ. х | − |
|
|
+ πп, n Z U х | − |
|
|
+ πп,п Z . |
|||
|
2 |
|
4 |
|
|
4 |
|
4 |
|
Упражнения
Решить неравенства (648-669):
648.sin x > − 1 . 2
649.sin x > 1. 3
650.cos x > 1 . 4
651.cos x > − 1 . 2
652.tgx ≥ 2.
653.tgx > −
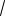 3.
3.
654.ctgx > −3.
655.ctgx > −
 3.
3.
656.sin х <  3 . 2 2
3 . 2 2
657.sin(х −1) ≤ −  3 .
3 .
2
658.cos 2x <  3 . 2
3 . 2
659.cos(x + 2) < −  3 .
3 .
2
660.tg(2x −1) <1.
661.tg3x < −1.
662.ctg x <1.
2
663.ctg(х −1) < −1.
664.2sin2 х − 7sin x + 3 > 0.
665.12cos2 x + 7sin x <13.
666.cos4x + cos2x < 0.
667.sin х + cos х > −
 2.
2.
668.2tgx ≤ 3tgx.
669.sin(cos х) > 0.
Решить неравенства с параметрами (670-678):
670. sin х > а. |
675. ctgх > a. |
|
671. cos x ≤ а. |
676. ctgх ≤ a. |
|
672. cos x > а. |
677. cos(аx + b) < с,а ≠ 0. |
|
673. tgx ≥ а. |
678.ctg(аx − b) ≥ с,а ≠ 0. |
|
674. tgx < а. |
||
|
124
§5. Решение систем тригонометрических уравнений и неравенств
Напомним основные сведения, необходимые для решения систем тригонометрических уравнений.
Две системы уравнений называют равносильными, если множества их решений совпадают. Если каждое решение первой системы является решением второй системы, то вторую систему называют следствием первой.
Отметим некоторые преобразования, которые приводят к системе, равносильной к данной или являющейся следствием данной. В качестве исходной рассмотрим систему
|
|
f (x, y) = |
g |
(x, y), |
|
|
1 |
1 |
(*) |
|
|
f2 (x, y) = g2 (x, y). |
||
1.Система f1(x, y) = g1(x, y), |
|
|
равносильна системе (*) |
|
f1(x, y) ± f2 (x, y) = |
g1(x, y) ± g2 (x, y) |
|||
2. Система |
|
|
|
|
f |
(x, y) = g |
(x, y), |
|
(**) |
1 |
1 |
|
|
|
f1(x, y) f2 (x, y) = g1(x, y)g2 (x, y)
является следствием системы (*). Система (**) равносильна системе (*), если не существует таких кортежей (x,y), на которых f1(x, y) и g1(x, y) одновременно обращаются в нуль.
3. Система
f (x, y) |
= g (x, y), |
|
||
1 |
|
1 |
(***) |
|
f1(x, y) |
= |
g1(x, y) |
||
|
|
g2 (x, y) |
|
|
|
|
|||
f2 (x, y) |
|
|
||
является следствием системы (*), если не существует таких кортежей |
||||
(x,y), на которых f2 (x, y) и g2 (x, y) одновременно обращаются в нуль. Если, кроме того, не существует таких кортежей, на которых f1(x, y) и g1(x, y) одновременно обращаются в нуль, то система (***) равносильна системе (*).
4. Если уравнение равносильно уравнению
f2 (x, y) = g2 (x, y)
(или является его следствием), то система
f1(x, y) = g1(x, y), |
|||
f |
′(x, y) = g′ |
(x, y) |
|
|
2 |
2 |
|
равносильна системе (*) (или является следствием системы (*)). 5. Если совокупность уравнений
f21(x, y) = g21(x, y); f22 (x, y) = g22 (x, y),...; f2k (x, y) = g2k (x, y)
равносильна уравнению |
f2 (x, y) = g2 (x, y) |
(или является его следстви- |
||||
ем), то совокупность систем |
|
|
|
|
|
|
f |
= g , |
|
f |
= g , |
|
f = g , |
1 |
1 |
1 |
1 |
…. 1 1 |
||
f21 = g21 |
f22 = g22 |
|
f2к = g2к |
|||
|
|
|
125 |
|
|
|

равносильна системе (*) (или является следствием системы(*)). Если, решая систему, мы преобразовали ее в систему, являющуюся
следствием исходной, то найденные решения новой системы, безусловно, подлежит проверке.
При решении систем тригонометрических уравнений, как и при решении систем алгебраических уравнений, кроме приемов, рассмотренных выше, применяются 3 основных метода:
1)линейного преобразования (или алгебраического сложения);
2)подстановки;
3)замены переменных.
Отметим также, что при решении систем тригонометрических уравнений часто оказывается удобнее вместо общих формул, по которым решаются уравнения вида
sin x = a,cos x = a,
записывать решения этих уравнений в виде совокупности двух семейств. Пусть, например, нужно решить систему уравнений
sin(x + y)= |
1 |
, |
|
|
||
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
(4.1) |
|||
|
|
|
|
|
||
|
|
|
||||
cos(x − y)= |
|
|
2 |
. |
||
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
||
Если воспользоваться общими формулами, то придем к системе
|
|
|
|
|
|
|
|
n π |
||||
|
|
|
х + у = |
(−1) |
|
6 + πn, n Z, |
||||||
|
|
|
|
|
|
|
π |
|
(4.2) |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
х − у = ± + 2πk,k Z |
|||||||||
|
|
|
|
|
|
|
4 |
|
|
|||
откуда находим: |
|
|
|
|
|
|
|
|
|
|
||
|
х |
= (−1) |
n π |
± |
π |
+ |
πn |
+ πk,(n,k Z), |
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||
1,2 |
|
12 |
|
8 |
|
2 |
|
|
||||
|
|
|
|
|
|
|
(4.3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
= (−1)n |
π |
m π |
+ πn − πk(n,k Z). |
|||||||
|
||||||||||||
|
1,2 |
|
12 |
|
8 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|||||
- решение системы (4.1). Если же не пользоваться общими формулами, т.е. если решение первого уравнения системы (4.1) записать в виде со-
вокупности
х + у = π + 2πn; х + у = 5π + 2πn, n Z, 6 6
а решение второго уравнения системы (4.1) записать в виде совокуп-
ности
x − y = π + 2πk |
или х − у = − π + 2πk, k Z, |
4 |
4 |
то мы получим совокупность 4-х систем:
126
