Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Педагогический Университет им. М. Акмуллы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Гайнуллин часть2

.pdf

Скачиваний:

Добавлен:

19.03.2015

Размер:

1.37 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 96 7 8 9 > Следующая >>>

Рассмотрим функцию у = cos х на отрезке 0 ≤ х ≤ π . Если −1≤ у ≤ 1 ,то на отрезке [0,π ] существует единственная дуга arccos у , косинус которой равен х. Следовательно, функция, обратная относительно у = cos х на отрезке 0 ≤ х ≤ π , выражается формулой

	х = arccos у , где −1≤ х ≤1.
Функция у = arccos х обладает следующими свойствами:
1)	Область определения функции у = arccos х есть отрезок −1≤ х ≤1.
2)	На отрезке −1≤ х ≤1 функция у = arccos х убывает от π до 0.
3)	Имеет место равенствоarccos(−х) = π − arccos х. Из этого тождества

следует, что функция у = arccos х не является ни четной, ни нечетной.

Рассмотрим функцию у = tgх на отрезке − π ≤ х ≤ π . Данная функция

2 2

в промежутке (0,π ), монотонно возрастает и непрерывна, следовательно, существует обратная функция, однозначная, непрерывная и строго монотонно возрастающая и выражается формулой

y = arctgx , где − ∞ ≤ х ≤ ∞ . Функция у = arctgх обладает следующими свойствами:

1) Область определения функции у = arctgх есть отрезок − ∞ ≤ х ≤ ∞ .

2) На отрезке − ∞ ≤ х ≤ ∞ функция у = arctgх возрастает от − π до π .

2 2

3) Имеет место равенство arctg(−х) = π − arctgх. Из этого тождества следует, что функция у = arctgх не является ни четной, ни нечетной.

137

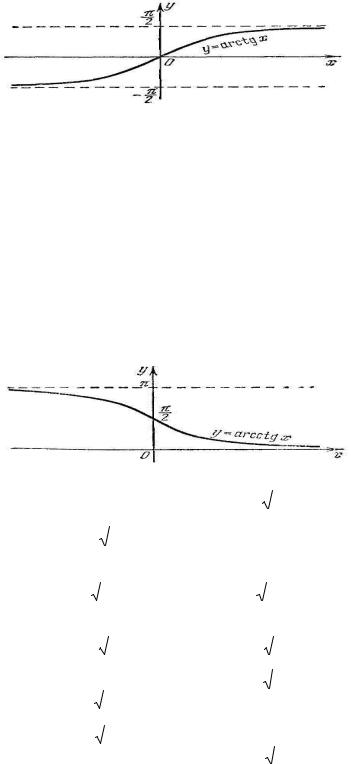
Рассмотрим функцию у = ctgх на отрезке 0 ≤ х ≤ π . Данная функция в

промежутке	− π ,π		, монотонно возрастает и непрерывна, следователь-
	2 2

но, существует обратная функция, однозначная, непрерывная и строго монотонно убывающая и выражается формулой

	y = arcctgx, где 0 ≤ х ≤ π .
Функция у = arcctgх обладает следующими свойствами:
1)	Область определения функции у = arcctgх есть интервал− ∞ ≤ х ≤ ∞ .
2)	На интервал − ∞ ≤ х ≤ ∞ функция у = arcctgх убывает от π до 0.
3)	Имеет место равенство arcctg(−х) = π − arcctgх. Из этого тождества

следует, что функция у = arcctgх не является ни четной, ни нечетной.

Тригонометрические операции над аркфункциями.

sin(arcsin х) = х

cos(arcsin х) = 1− х2

cos(arccos х) = х

sin(arccos х) = 1− х2

sin(arctgх) =

cos(arctgх) =

1+ х2

sin(arcсtgх) =

cos(arcсtgх) =

1+ х2

tg(arcsin х) =

ctg(arcsin х) =

1− х2

tg(arccosх) =

1− х2

ctg(arccos х) =

1− х2

tg(arctgх) = х

ctg(arctgх) =

tg(arcсtgх) =

ctg(arcсtgх) = х

138

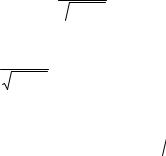
Соотношения между аркфункциями. 1.Выражение arcsin х через арктангенс.

arcsin х = arctgх в интервале (-1,1).

1− х2

2.Выражение arctgх через арксинус.

arctgх = arcsin	х	в интервале (−∞,+∞).
	1+ х2

3.Выражение арккосинуса через арккотангенс.

arccos х = arctg .

1+ х2

Пример 1. Решить уравнение

2arcsin x = a +

а2

(1)

arcsin x

Решение. Положим t = arcsin x . Тогда:

(2t + a)(t − a)

t = a,

а2

2t2 − аt − а2

t = −

2t = a +

= 0

t ≠ 0

t = a,

t = −

а ≠ 0.

а ≠ 0

−

≤ −

≤

−

≤ а ≤

arcsinx = a,

2 2

−π ≤ а ≤π,

(1) arcsinx = −

≠ 0,

а ≠ 0,

≠ 0

= sinа

а ≠ 0

= sin

−

х = −sin

≤ а ≤

−

≠ 0,

= sinа.

Ответ. Если а

−

,0 U (0,π ] , то

− sin

,sin a ;

если а [−π ,−π ) U (π ,π ], то

− sin

; если а (−∞,−π ) U (π ,∞) , то Ш.

Пример 2. Решить неравенство

3arctg2 x − 4πarctgx +π 2 > 0.

(1)

Решение. Положим у = arctgx . Тогда:

< y <

− π < y < π ,

< y <

−

3у2 − 4πу

+π 2 > 0

−

у <

3 у

(у −π )> 0

139

	π	< y <	π	,		π		π
−	2		2		−		< y <		.
						2		3
π	< y

(1) − π < arctgx < π −∞ < х < 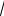3.

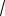Ответ. (−∞,3).

Пример 3. Решить неравенство

2arccos2 x − 5aarccos x + 2a2 < 0,а ≥ 0.

(1)

Решение. Положим t = arccos x . Тогда:

а > 0,

а = 0,

− 5at

+ 2a

< 0

(2t − a)(t − 2a)< 0

< t < 2a,

2 < 0

0 ≤ t ≤ π .

а > 0,

0 < a ≤

π < а < 2π

а = 0,

> 0,

2a > π ,

а = 0

2a ≤ π ,

< t ≤

π ,

< t

< t ≤ π.

< t < 2a

< π

0 < a ≤ π ,

π < а < 2π

0 < a ≤ π ,

π < а < 2π ,

(1)

< arccos x < 2a

< arccos x ≤ π

cos2a < x < cos

−1≤ x < cos

Ответ. Если 0 < a ≤ π , то

(cos2a,cos

) ; если π < а < 2π , то[−1,cos

);

если а = 0 или

а ≥ 2π , то .

Пример 4. Решить уравнение

arccos

= 2arctg(х −1).

(1)

Решение. Первый способ. Возьмем косинус от обеих частей данно-

го уравнения:

сos arccos

= cos(2arctg(х −1)).

(2)

Уравнение (2) является следствием уравнения (1), т.е. (1) (2).

Воспользуемся формулой сos2α =	1	−tg2α	для преобразования правой
		+ tg2α
1

части уравнения (2). (Заметим, что α = arctg(х −1) (− π ,π ) , поэтому tgα су-

2 2

ществует). Тогда уравнение (2) равносильно уравнению

х = 1− (х −1)2 . 2 1+ (х −1)2

140

Решая последнее уравнение, найдем: х = 0; х = ±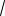2 . Так как (1) (2), то следует проверить, какие из корней уравнения (2) являются решениями уравнения (1).

Проверка.

1)	х = 0:arccos0 ≠ 2arctg(−1), так как	arccos0 =	π	π		= −	π
1)	х = 0:arccos0 ≠ 2arctg(−1), так как	arccos0 =		,2arctg(−1) = 2		= −	.
			2		4		2


				2				2

2)	х = −		−		≠ 2arctg(− 2 −1) , так как	arccos	−		> 0	, а

		2 :arccos
				2				2
				2				2

2arctg(− 2 −1) < 0 .

3) х = 2 :arccos

= 2arctg(

2 −1);

= 2arcctg( 2 −1) .

Так

как

0 <

2 −1< 1 arctg(

2arctg( 2

−1)

2 −1) 0,

cos π = cos(2arctg(

−1)),

х = 2 -

корень

уравнения

(2),

т.е.

то

π = 2arctg(

2 −1) .

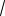Ответ. {2}.

Второй способ.

arccos			x	= 2arctg(х −1).	(1)

		2
	x	= tg(2arctg(х −1))
tg arccos					(2)

	2

Так как	tgα =	1− cos2	α	, где α = arccos	x	, и tg2β =	2tgβ	, где
		cosα					1− tg2β
				2

β = arctg(х −1), то уравнение (2) равносильно уравнению

≥ 0,

х2

1−

х −1)

2(х −1)

4 − х

х −1

− х

≥ 0,

1− (х −1)

2 − х

х −1)2

4 − х2

− х)

1≤ х < 2,

х4

− 4х3 + 4х2 + 8х −12

= 0

1 ≤ х < 2,

(х4

− 2х2 )

+ (6х2 −12)−

4х3 + 8

х = 0

(х2

− 2)(х2 − 4х + 6)= 0; откуда х = 2.

Подстановкой х = 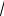2 в обе части уравнения (1) убедимся, что х = 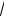2 - решение уравнения (1).

141

Остается выяснить, не произошла ли потеря решений уравнения (1) при переходе к уравнению (2). Для этого достаточно решить систему:

arccos

= π ,

= 0,

2 2

−

2arctg(х −1)

arctg(−1)

которая не имеет решений, значит, нет решений уравнения (1) при переходе к уравнению (2). Ответ. {2}.

Простейшие неравенства, содержащие обратные тригонометрические функции, решаются, опираясь на свойства обратных тригонометрических функций.

Упражнения

Решить уравнения (705-713):

705. arcsin x =

709. arcsin x = π.

710. 3arcsin x = π.

706. arctgx = −

711. 3arccos(x +1) = 2π.

712. cos(4arccos x) = −

707. arcсtgx = −

713. arcsin x + arccos(х −1) = π.

708. arccosx = 3.

Решить неравенства (714-736):

714. arcsin x ≤ 3.

726. arctgx < −2.

715. arcsin x < −2.

727. arcctgx >

5π

716. arcsin x > −1.

728. arcctgx <

6π

717. arcsin x < π .

729. arcctgx > 2.

718. arccosх ≤ 0.

730. arctg

>1.

719. arccos х > π .

731.arctg(−3х) >1.

720. arccos х ≤ arccos

732.arccos

≤ π .

−

721. arccosх > −1.

733. arccos

2х

≥ π .

х2 +1

722. arccos х >

734. arcsin(log2 х) ≥ 0.

723.arctgx > − π .

735.arcsin(х2 +1) < 2.

724. arctgx ≥ 2.

736.arcsin(х2 − 3) > π .

725. arctgx < π .

142

ГЛАВА VI.

РЕШЕНИЕ НЕКОТОРЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ С ПАРАМЕТРАМИ

§ 1. Общие сведения

Пусть дано уравнение

f (х,а) = g(х,а).

(1)

Если ставится задача отыскать все такие пары (х,а) , которые удовлетворяют данному уравнению, то мы имеем уравнение с двумя переменными х и а . Но можно поставить и другую задачу. Дело в том, что если придать переменной а .какое-либо фиксированное значение, то уравнение (1) можно рассматривать как уравнение одной переменной х , причем решения этого уравнения, естественно, определяются выбранным значением а . Если ставится задача для каждого значения а из некоторого числового множества А решить уравнение (1) относительно х , то уравнение (1) называют уравнением с одной переменной и одним параметром а , а множество А- областью изменения параметра. Условимся всюду в настоящем параграфе уравнение (1) понимать не как уравнение с двумя переменными, а как уравнение с одной переменной х и одним параметром а .

Уравнение (1)- это по существу краткая запись семейства уравнений, получающихся из уравнения (1) при различных конкретных числовых зна-

чениях параметра. Пусть, например, дано уравнение 2а(а − 2)х = а − 2,		(2)
и пусть область изменения параметра А = {−1,0,1,2,3}.	тогда уравнение (2)
	6х = −3при − а = −1,
	0 х = −2при − а = 0,

есть краткая запись следующего семейства уравнений:
есть краткая запись следующего семейства уравнений:	− 2х = −1при − а = 1,
	0 х = 0при − а = 2,

	6х = 1при − а = 3.

Условимся всюду в дальнейшем под областью изменения параметра подразумевать (если не сделано специальных оговорок) множества всех действительных чисел, а задачу решения уравнения с параметром формулировать следующим образом: решить уравнение (1) с параметромэто значит решит (на множестве действительных чисел) семейство уравнений, которые получаются из уравнения (1) при различных действительных значениях параметра.

Так как выписать отдельно каждое уравнение бесконечного семейства невозможно, то обычно стремятся выделить «особые» значения параметра (мы будем называть их контрольными), в которых или при переходе через которые происходит качественное изменение уравнения. Чтобы пояснить, как находятся контрольные значения параметра, рассмотрим несколько параметров.

143

§2. Решений уравнений с параметрами

Пример1. Решим уравнение

2а(а − 2)х = а − 2.

(3)

Решение. Здесь контрольными будут те значения параметра а , при которых коэффициент при х , в то время как при остальных значениях параметра такое давление возможно. Значит, целесообразно рассмотреть уравнение (3) при следующих значениях параметра:

а ≠ 0,

1) а = 0; 2) а = 2; 3)

а ≠ 2.

При а = 0 уравнение (3) принимает вид 0 х = −2. Это уравнение не имеет решений. При а = 2 уравнение (3) принимает вид 0 х = 0. Решением этого уравнения служит любое действительное число. Если а ≠ 0 и а ≠ 2, то

из уравнения (3) получаем	х =		а − 2		откуда находим, что х =				1	.
из уравнения (3) получаем	х =	2а(а −			откуда находим, что х =					.
		2а(а −		2)					2а
Ответ: при а = 0;	(−∞,∞) при а = 2;					1	при а ≠ 0,
Ответ: при а = 0;	(−∞,∞) при а = 2;						при а ≠ 0,
						2а	а ≠ 2.
Пример 2. Решим уравнение
	(а −1)х2 + 2(2а +1)х + (4а + 3) = 0.							(4)
Решение. В данном случае			контрольным является значение а =1:
при а ≠ 1 уравнение (4) является квадратным, а при а =1								оно линейно

(происходит качественное изменение уравнения). Значит, для уравнения

(4) целесообразно рассмотреть следующие случай: 1) а =1; 2) а ≠ 1.

		При а =1	уравнение (4) принимает вид 6х + 7 = 0, откуда находим
х = −	7	.
х = −		.
6
		В случае	а ≠ 1 для квадратного уравнения (4) выделим те значения

параметра а при которых дискриминант уравнения обращается в нуль (вторые контрольные значения параметра). Составим дискриминант урав-

нения (4): D = (2а +1)2 − (а −1)(4а + 3), откуда D = 5а + 4. 4 4

Из условия D = 0 находим а = − 4 . Если а < − 4 . То D < 0; если

5	5
	4
а ≥ −		,
а ≥ −		,
	5
	тоD ≥ 0.
а ≠ 0,	тоD ≥ 0.

Значит осталось решить уравнение (4) в каждом из следующих двух

			4
случаев: а < −	4	а ≥ −		,
	4	а ≥ −		,
		;	5
	5	;	5
	5
		а ≠ 1.

144

Если а < − 4 , то уравнение (4) не имеет (действительных) решений;

если

а ≥ −

, то находим:

− (2а +1) ± 5а + 4

х1,2

−1

а ≠ 1

Ответ: при а < −

−

при а =1

− (2а +1) ±

5а + 4

при

а ≥ −

;

а −1

а ≠ 1.

Пример 3. Решим уравнение

х2 +1		−	1	=	х		(5)
						.
а2	х − 2а		2 − ах
					а

Решение. Первым контрольным значением параметра является значение а = 0. В этом случае уравнение (5) не имеет корней. Рассмотрим случай, когда а ≠ 0. После преобразований уравнение (5) примет вид

				(1− а)х2 + 2х + а +1= 0 .						(6)
Приравняв к нулю коэффициент при х2 , найдем второе контрольное
значение параметра:		а =1. При а =1				уравнение (6) принимает				вид
2х + 2 = 0 ,откуда находим: х = −1.					Если а ≠ 0 и а ≠ 1, то из квадратного урав-

нения (6) получаем: х		=	−1± а2		, т.е. х	= −1, х		=	а +1
нения (6) получаем: х	1,2	=	1− а		, т.е. х	= −1, х		=	а −1.
	1,2		1− а		1		2		а −1.

Проверка. Уравнения (5) и (6) равносильны при х ≠ 2 . Следовательно

из найденных решении уравнения (6) мы должны исключить значение

х = 2 . Если а =1, то 2 = 2 . Значит полученное выше при а =1 решение х = −1

а а

не является посторонним.

В случае а ≠ 1,

мы получили: х = −1,

х2

а +1

. Выясним, при каких

а ≠ 0

а −1

значениях параметра выполняется равенство х

Полагая −1=

находим а = −2 . Это значит, что если а = −2 , то

= −1 - посторонний корень. В этом случае х

а +1

− 2 +1 =

а −1

− 2 −1 3

Выясним, при каких значениях параметра выполняется неравенство

Имеем	а +1	=	2	, откуда а2 − а + 2 = 0 .
	а −1		а

145

Последнее уравнение не имеет действительных решений. Это значит,

что х

а +1

ни при каких значениях параметра не является посторонним

а −1

корнем.

Ответ: при а = 0; -1 при а =1;

при

а = −2 ; х = −1,

а +1

при

а −1

а ≠ −2,

а ≠ 0,а ≠ 1.

Пример 4. Решим уравнение


х + а = 1− (х + а).						(7)

Решение. Здесь а = 0- контрольное значение параметра (при а < 0 левая часть уравнения не имеет смысла, а при а ≥ 0 - имеет). Поэтому для уравнения (7) целесообразно рассмотреть следующие случай: 1) а < 0 ; 2)

а ≥ 0 .

Ясно, что при а < 0 уравнение (7) не имеет решений (иными словами, любое уравнение семейства уравнений, кратко записанного в виде (7), соответствующее отрицательному значению параметра а не имеет смысла, т.е. не имеет решений). Приа ≥ 0 , выполнив возведение обеих частей уравнения (7) в квадрат и последующее упрощения, придем к уравнению


2 ах =1− 2х − 2а .			(8)

Здесь мы не обнаруживаем никаких новых контрольных значений параметра. Снова выполнив возведение обеих частей уравнения в квадрат и последующие упрощения, получим квадратное уравнение

4х2 + 4х(а −1) + 4а2 − 4а +1= 0.							(9)
Составим дискриминант:	D	= (2)а −1))2 − 4(4а2 − 4а +1).
Составим дискриминант:		= (2)а −1))2 − 4(4а2 − 4а +1).
4
Приравняв его к нулю, находим: а = 0,а				=	2	− вторые контрольные
Приравняв его к нулю, находим: а = 0,а				=		− вторые контрольные
1			2		3
значения параметра. Заметим, что D < 0 , если а >				2	(напомним, что мы рас-
значения параметра. Заметим, что D < 0 , если а >				3	(напомним, что мы рас-
				3

сматриваем случай а ≥ 0 ). Таким образом, целесообразно рассмотреть следующие случай: а > 2 ;0 ≤ а ≤ 2 .

Впервом случае уравнение (9) не имеет решении, во втором

х =	1− а ±	2а − 3а2
			.
			.
1,2		2
		2

Выше мы отмечали, что при а < 0 уравнение (7) не имеет решений. Значит, для уравнения (7) мы пришли к следующему результату: если

а < 0 ; а > 2 , то решений нет; если 0 ≤ а ≤ 2 , то решениями уравнения (7) мо-

гут быть значения:

146

<<< < Предыдущая 1 2 3 4 56 / 96 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.03.2015396.29 Кб55Все формулы площади плоских фигур.doc
#
09.11.2019216.58 Кб1Высшая математика лекции.doc
#
13.08.2019743.42 Кб5Г. В. Ф. Гегель Философская пропедевтика.doc
#
13.08.2019628.74 Кб3Г.В. Андрейченко, В.Д. Грачев - Философия (2001...doc
#
07.03.201642.9 Кб15Газизова Л.Ф., Нухова М.В. Психологические особенности стилей воспитания в родных и приемных семьях.docx
#
19.03.20151.37 Mб32Гайнуллин часть2.pdf
#
07.03.2016168.96 Кб22гак лексикология 1.doc
#
18.03.2015127.91 Кб27ГАК.docx
#
19.11.201866.38 Кб5ГАЛАКТИКА.docx
#
03.11.20181.8 Mб2галина.doc
#
27.11.2019336.38 Кб6ГГГ.doc