Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Педагогический Университет им. М. Акмуллы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

M3_10_13

.pdf

Скачиваний:

Добавлен:

19.03.2015

Размер:

890.87 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «Заочная физико-техническая школа

Московского физико-технического института (государственного университета)»

МАТЕМАТИКА

Последовательности. Пределы

Задание №3 для 10-х классов

(2013 – 2014 учебный год)

г. Долгопрудный, 2013

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы

Составитель: Е.Ю. Редкозубова, ассистент кафедры высшей математики МФТИ.

Математика: задание №3 для 10-х классов (2013 – 2014 учебный год), 2013, 32 с.

Дата отправления заданий по физике и математике – 30 ноября 2013г.

Составитель:

Редкозубова Елена Юрьевна

Подписано 17.09.13. Формат 60×90 1/16. Бумага типографская. Печать офсетная. Усл. печ. л. 2,0.

Уч.- изд. л. 1,77. Тираж 600 Заказ №13-з.

Заочная физико-техническая школа Московского физико-технического института (государственного университета)

ООО «Печатный салон ШАНС»

Институтский пер., 9, г. Долгопрудный, Москов. обл., 141700, ЗФТШ, тел./факс (495) 408-5145 – заочное отделение,

тел./факс (498) 744-6351 – очно-заочное отделение, тел. (499) 755-5580 – очное отделение.

e-mail: zftsh@mail.mipt.ru

Наш сайт: www.school.mipt.ru

2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы

§1. Бесконечные числовые последовательности

Определение. Бесконечной числовой последовательностью (или просто последовательностью) называется числовая функция x = x(n) ,

определѐнная на множестве N натуральных чисел.

Аргумент n этой функции записывается в виде индекса, т. е. вместо

записи		x(n)			используют запись xn , а саму последовательность часто
обозначают (xn ) . Число xn										называют n -м (читается: энным) членом
последовательности (xn ) . Приведѐм примеры.
(1)	1	; 1; 1; ... (т. е. xn = 1 для всех n N );
(2)	12 ;		22 ; 32 ; ... (т. е.					x	= n2 для всех n N );
								n
(3)	1	;	1	;	1	; ... (т. е. x		=		1	для всех n N );
							n
			2		3					n

(4)последовательность, n -й член которой равен n -му знаку после запятой в десятичной записи числа 338 ;

(5)последовательность, n -й член которой равен количеству простых чисел, не превосходящих n ;

(6)x1 = 1, x2 = 1, xn = xn 1 xn 2 для всех n 3

(последовательность Фибоначчи).

Как видим, последовательности задаются различными способами. Например, указывается формула n -го члена (примеры (1) – (3)). Закон

соответствия между номером n и членом xn может быть описан

словесно (примеры (4) – (5)). Последовательность может быть также задана рекуррентным соотношением: даны несколько первых членов последовательности и формула, выражающая следующие члены последовательности через предыдущие (пример (6)).

Легко убедиться, что в примере (4) x1 = 2 , x2 = 4 , x3 = 2 , x4 = 4 и

т. д., т. е. xn = 3 ( 1)n . В примере (6) формулу n -го члена найти сложнее:

2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы

						n					n
		1	1		5	n	1		5		n
		1	1		5		1		5


xn	=	5		2				2		.
		5		2				2

А вот явную формулу n -го члена последовательности (5) написать невозможно. Тем не менее, многие еѐ свойства установлены и без формулы.

Скажем несколько слов о геометрическом изображении последовательности. Поскольку последовательность (xn ) является функцией, то

геометрически еѐ можно изобразить графиком (рис. 1 а). Однако чаще всего члены последовательности изображаются точками координатной прямой, снабжѐнными соответствующими пометками (рис. 1 б).

x x1

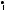
x2
x3
x5
O 1 2 3 4 5	n	n	0 xn x4x3 x2	x
O 1 2 3 4 5	n		0 xn x4x3 x2	x1
а)			б)

Рис. 1

Вопрос. Каким общим свойством обладают последовательности (1), (2), (5) и (6)?

Ответ. Каждый их член, начиная со второго, не меньше предыдущего.

Определение. Последовательность (xn ) называется строго возрастающей, если каждый еѐ член, начиная со второго, больше предыдущего, т. е. xn 1 > xn для любого n N . Последовательность (xn ) называется строго убывающей, если xn 1 < xn для любого n N . Последовательность (xn ) называется нестрого убывающей, если xn 1 xn для любого n N . Последовательность (xn ) называется

нестрого возрастающей, если xn 1 xn для любого n N .

2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы

Все такие последовательности (строго возрастающие, строго убывающие, нестрого убывающие, нестрого возрастающие) называются

монотонными.

Пример 1.1. Выяснить, является ли монотонной последовательность

Решение.

Уточним, чему равен

xn 1 . Для этого вместо n в

подставим n 1, т. е.

3(n 1)

. Рассмотрим разность

n 1

n 3

3(n 1)

3[(n 1)(n 2) n(n 3)]

n 1

n 3

n 2

(n 2)(n 3)

> 0,

(n 2)(n 3)

значит,

xn 1

> xn для любого n N . По определению последователь-

ность (xn ) является строго возрастающей.

Приведѐнные рассуждения являются стандартными при доказательстве монотонности последовательности. Используя особенности последовательности (xn ) , можно установить еѐ возрастание более простым

способом. Запишем x

в виде

x =

3n 6 6

= 3

, тогда

n 2

xn 1 = 3

> 3

= xn .

n 3

Пример 1.2. Выяснить, является ли монотонной последовательность

xn = 3 ( 1)n .

Решение. Последовательность не является монотонной, поскольку x2m 1 = 2 < 4 = x2m и x2m = 4 > 2 = x2m 1 для всех натуральных m .

Вопрос. Каким общим свойством обладают последовательности (1),

(3) и (4)?

Ответ. Все их члены лежат на отрезке [0; 4] .

Определение. Последовательность (xn ) называется ограниченной,

если существует число C > 0 такое, что для любого натурального n выполняется неравенство | xn | C .

2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы

Пример 1.3. Доказать, что последовательность (xn ) является огра-

ниченной тогда и только тогда, когда все еѐ члены лежат на некотором отрезке.

Решение. Пусть последовательность (xn ) ограничена. Тогда существует число C > 0 такое, что | xn | C для любого n N. Последнее неравенство можно переписать в виде C xn C, т. е. xn [ C; C]. Обратно, пусть все члены (xn ) лежат на некотором отрезке [m; M ]. Выберем симметричный отрезок [ C; C], содержащий [m; M ], тогда

C xn	C и,			следовательно,			\| xn \| C. В качестве такого C можно
взять, например,				max{\| m \|, \| M \|}.
Пример 1.4. Выяснить,						является ли ограниченной последователь-
ность x	=	10( 1)n n			.
			n2 1
n
Решение. Рассмотрим						\| x \|=		10n	. Поскольку при уменьшении

						n		n2 1

знаменателя положительной дроби значение дроби увеличивается, имеем:

\| x	\|=		10n	10n	=	10		10.

		n2 1		n2
n							n
Значит, \| xn \| 10 для любого			n N . По			определению последова-

тельность (xn ) является ограниченной.

Пример 1.5. Выяснить, является ли ограниченной последовательность xn = n2 .

Решение. Предположим, что последовательность (xn ) является ограниченной. Это означает, что существует такое число C > 0, что при

всех n выполняется неравенство | n2 | C. Однако при n > C 1 неравенство не выполняется. Следовательно, предположение неверно, т. е. последовательность (xn ) не является ограниченной.

§2. Арифметические и геометрические прогрессии

Рассмотрим подробнее два важных класса числовых последовательностей.

2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы

Определение. Последовательность (xn ) , каждый член которой, на-

чиная со второго, равен предыдущему, сложенному с одним и тем же числом d , называется арифметической прогрессией. Число d разность прогрессии.

Таким образом, арифметическая прогрессия есть последовательность, заданная рекуррентно равенством xn 1 = xn d и первым чле-

ном x1 .
Перечислим основные свойства арифметической прогрессии.
1) Формула n -го члена арифметической прогрессии:
xn = x1 (n 1)d,	n N.	(2.1)

2) Для конечной арифметической прогрессии x1, x2 , , xn суммы членов, равноотстоящих от концов, равны:

x1 xn = x2 xn 1 = x3 xn 2 =
= xk xn k 1,					k = 1, 2, , n.			(2.2)
3) Формула суммы n первых членов арифметической прогрессии:
S			=	x1 xn		n,		(2.3)
S	n		=			n,		(2.3)
	n				2
					2
или, учитывая 1),
Sn =		2x1 (n 1)d					n.	(2.3`)
Sn =					2		n.	(2.3`)
					2

Приведѐм ещѐ характеристическое свойство арифметической прогрессии.

4) Последовательность (xn ) является арифметической прогрессией

тогда и только тогда, когда каждый член последовательности, начиная со второго, равен среднему арифметическому соседних членов:

x =	xn 1 xn 1	,	n 2.	(2.4)

n	2

В 9 классе свойства 1) – 3) были доказаны, поэтому приведѐм доказательство лишь свойства 4). Пусть дана арифметическая прогрессия

(xn ) , тогда при n 2

имеем xn = xn 1 d и xn = xn 1 d . Складывая

почленно эти равенства, получаем 2xn = xn 1 xn 1 . Обратно, пусть для n -го члена (xn ), n 2 , выполнено равенство (2.4) , тогда

2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы

2xn = xn 1 xn 1		или	xn 1 xn	= xn xn 1 . Отсюда	получаем, что
xn 1 xn = x2	x1 , т. е.		любые два соседних члена последовательности
отличаются	на	одно	и то же	число d = x2 x1 .	По определению

последовательность (xn ) является арифметической прогрессией.

	Пример 2.1. Найти сумму первых 10 членов арифметической про-
грессии, если x5 x6 = 4.
	Решение. По формуле (2.3)			S	=	x1 x10		10	. Заметим, что члены x
	Решение. По формуле (2.3)			S	=			10	. Заметим, что члены x
				10	2				5
					2
и	x6	равноотстоят от x1		и	x10 соответственно. По (2.2)
x x		= x	x , следовательно, S		=	4	10 = 20 .
x x		= x	x , следовательно, S		=		10 = 20 .
1	10	5	6	10

Ответ. 20.

Определение. Последовательность (xn ) , первый член которой отли-

чен от нуля и каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же отличное от нуля число q , называется

геометрической прогрессией. Число q знаменатель прогрессии.

Таким образом, геометрическая прогрессия есть последовательность, заданная рекуррентно равенством xn 1 = xn q , первым членом

x1 0 и знаменателем q 0 .

Перечислим основные свойства геометрической прогрессии. 1) Формула n -го члена геометрической прогрессии имеет вид

x	= x qn 1	, n N.	(2.5)
n	1
2) Для конечной геометрической прогрессии			x1, x2 , , xn произ-

ведения членов, равноотстоящих от концов, равны:

x1 xn = x2 xn 1 = x3 xn 2 = =

= xk xn k 1, k = 1, 2, , n. (2.6)

3) Формула суммы n первых членов геометрической прогрессии:

S		= x	1 qn		при q 1 и	S		= n x	при q 1.
				q
	n	1 1					n	1

Приведѐм ещѐ характеристическое свойство геометрической прогрессии.

2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы

4) Числовая последовательность (xn ) ненулевых членов является

геометрической прогрессией тогда и только тогда, когда модуль каждого еѐ члена, начиная со второго, равен среднему геометрическому соседних членов:


	xn	=		xn 1 xn 1 ,			n 2,	(2.8)
или
	(x )2		= x		x	,	n 2.	(2.8`)
	n			n 1	n 1

Докажем свойство 4). Пусть последовательность (xn ) является гео-

метрической прогрессией, тогда x2

= (x qn 1 )2

= x qn 2 x qn

= x

n 1

Обратно, пусть все члены последовательности (xn )

отличны от нуля и

для n -го еѐ члена,

n 2 , выполнено

= x

, тогда

xn 1

n 1

xn 1

Следовательно,

xn 1

, или

= x q ,

где q =

. По определению

n 1

последовательность (xn ) является геометрической прогрессией.

Пример 2.2. Известно, что

x1, x2 ,

xn геометрическая прогрес-

сия. Известны числа

S = x x

и T =

. Найти

P = x1 x2

xn .

Решение. Обозначим знаменатель прогрессии через q . Преобразуем

искомую величину
	x x x = x x q x qn 1											= xnq1 2 n 1				=
	1	2	n	1	1				1		1
					n(n 1)							n
			= xnq		2		= (x2qn 1)				2		.
				1				1
Пусть	q 1,		тогда			S = x			qn 1			.		Последовательность
Пусть	q 1,		тогда			S = x						.		Последовательность
								1	q 1
1 / x1, 1 / x2 ,	,	1 / xn	является геометрической прогрессией со знаме-
нателем 1/ q . Следовательно,					T =	1		1 q n		,	т. е.			T =	1	qn 1		.
						x 1 q 1									x qn	1 (q	1)
						1									1

2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы

Отсюда заключаем, что S/T = x12qn 1 . Последнее равенство, очевидно,

справедливо и при q = 1. Следовательно, P = S n /T n .

Ответ. S n /T n .

Пример 2.3. Три положительных числа образуют возрастающую арифметическую прогрессию. Если среднее из них уменьшить на 40%,

то получится геометрическая прогрессия, сумма членов которой равна 39. Найти эти числа.

Решение. Обозначим данные числа x1 , x2 , x3 . По условию сумма

x1 0,6x2	x3 равна 39. По характеристическому свойству арифмети-
ческой	прогрессии	2x2 = x1 x3	и,	следовательно,
x1 0,6x2	x3 = 2,6x2 . Отсюда получаем, что		x2 = 15 .	По характерис-

тическому свойству геометрической прогрессии (0,6x2 )2 = x1 x3 . Итак,

x1 x3 = 30 и	x1 x3 = 81, т. е. по обратной теореме Виета x1	и x3 явля-
ются корнями	уравнения x2 30x 81 = 0 . Корни этого	уравнения
равны 3 и 27,	следовательно, x1 = 3 и x3 = 27 , поскольку последо-

вательность x1, x2 , x3 по условию является возрастающей.

Ответ. 3 , 15 и 27.

Пример 2.4. Найти формулу n -го члена последовательности, задан-

ной рекуррентно: x =

; x

= 2x 1 , n N.

n 1

Решение.

Рассмотрим

вспомогательную

последовательность

yn = xn a , где число

подбирается так, чтобы последовательность

была

геометрической

прогрессией.

Подставляя

xn = yn a и

xn 1 = yn 1

рекуррентное

соотношение,

имеем

yn 1

a = 2( yn a) 1,

т.

е.

yn 1 = 2yn (1 a) .

Последовательность

будет

геометрической

прогрессией,

если

1 a = 0 , т. е.

a = 1.

Поскольку

y = x a =

формула общего

члена

геометрической

2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.05.2019135.67 Кб32Lektsii_po_PED_TEKhNOLOGIYaM.docx
#
18.03.2015827.9 Кб43lektsii_po_pravovedeniyu.doc
#
18.03.201533.38 Кб29lektsii_Skalina (1).docx
#
18.03.201547.62 Кб43Lexical and syntactical Stylistic Devices.doc
#
18.03.2015100.86 Кб12Leybnits_Monadologia.doc
#
19.03.2015890.87 Кб19M3_10_13.pdf
#
19.03.2015122.71 Кб41Mantry_s_perevodami.pdf
#
18.03.2015130.05 Кб2Mark_K_Nischeta_filosofii.doc
#
18.03.2015145.39 Кб21matematika(1).docx
#
18.03.201583.98 Кб7matematika.docx
#
15.11.20181.38 Mб19MATLAB 4-ая методичка МиграноваНГ.doc