
M3_10_13
.pdf
2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
прогрессии |
y |
|
запишется так: y |
|
= |
3 |
2n 1 |
( y = |
3 |
, q = 2) . Тогда |
|
|
n |
|
n |
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|||
x = y a = 3 2n 2 |
1, n 2 . |
|
|
|
|
|
|
|
||
n n |
|
|
|
|
|
|
|
|
|
|
Ответ. x |
= 3 2n 2 1, n 2 . |
|
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
|
§3. Предел последовательности
При увеличении n члены последовательности xn = 1 / n становятся сколь угодно малыми, неограниченно приближаются (стремятся) к нулю. Логично считать, что ноль – предел последовательности (xn ) .
Однако такого интуитивного понимания в более сложной ситуации может оказаться недостаточно. Мы должны точно сформулировать, что означает слово «предел» на языке чисел. Строгое определение предела было сформулировано довольно поздно – только в середине XIX века. Дело в том, что в отличие от используемых ранее «назывных» определений (типа определения равнобедренного треугольника) здесь описывается процесс изменения величины: пробегая по ряду натуральных чисел 1, 2 , 3, , n, , мы наблюдаем за поведением xn . Такие
понятия плохо формализуются.
Попытаемся понять, что следует предпринять, чтобы проконтролировать утверждение « xn стремится к a ». Изобразим члены
последовательности на числовой оси и отметим на ней точку a . Представим ситуацию образно: будем делать фотографии a каждый раз с новым оптическим увеличением. Число a будет пределом после-
довательности xn , если a «друг» xn : на любой такой фотографии окажутся все xn , начиная с некоторого номера.
Проиллюстрируем сказанное на примере последовательности xn = 1/ n . В качестве «фотографии» a = 0 можно взять симметричный интервал ( , ) 1. Оптическому увеличению соответствует умень-
шение . |
Пусть |
k 1 / , |
тогда 1/ n < при n > k и, следовательно, |
||
член xn попадает на «фотографию», |
т. е. |
< xn < . Например, при |
|||
=1 / 100 |
все |
члены |
x101,x102 , |
, |
окажутся в интервале |
1 греческая буква «эпсилон».
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
11

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
( 1/100, 1/100) , |
при = 1 / 1000 уже только члены |
x1001 , x1002 , , |
окажутся в интервале ( 1/1000, 1/1000) и т. д. |
|
|
Определение. |
Число a называется пределом последовательности |
|
(xn ) , если для |
любого положительного числа |
найдѐтся такое |
действительное число k , что при всех n > k выполняется неравенство
| xn a |< . |
(3.1) |
В этом случае пишут lim xn = a (читается: предел |
xn при n , |
n |
|
стремящемся к бесконечности, равен a ). Последовательность, имеющая конечный предел, называется сходящейся, в противном случае – расходящейся.
Выясним геометрический смысл понятия предела. Для положительного числа интервал (a , a ) называется - окрестностью
точки a . Неравенство (3.1) равносильно двойному неравенству
< xn a < или
a < xn < a . |
(3.2) |
Неравенство (3.2) показывает, что все члены последовательности (xn ) с номерами n > k попадают в окрестность точки a . В
определении предела число может быть любым (сколь угодно малым), поэтому произвольная (сколь угодно малая) окрестность точки a
содержит все члены (xn ) за исключением, быть может, конечного числа (рис. 2а). На уровне графика последовательности это означает,
x
a+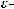



 a
a
a-





|
|
|
|
xn+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x1 |
x2 |
a- xn a |
a+ |
x3 |
|
x |
|
O |
1 2 |
3 |
|
n |
n+1 |
n |
|||||||||||||||
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
|
|
|
x = a и |
||||||
что |
вне |
сколь |
угодно |
узкой |
|
|
полосы |
между |
прямыми |
||||||||||||||||||||
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
12

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
x = a может оказаться лишь конечное число точек графика (xn )
(рис. 2б).
Замечание. В определении предела выбор числа k , вообще говоря, зависит от . Чтобы подчеркнуть это, иногда пишут k = k( ).
Доказать, что последовательность (xn ) имеет предел, фактически
означает найти функциональную зависимость k от . Вообще, определение предела по виду напоминает нескончаемую дискуссию между двумя лицами A и B : A задаѐт точность приближения , в ответ B указывает число k , с которого эта точность достигается, т. е. выполняется неравенство (3.1) при всех n > k; A уменьшает точность,
B указывает новое k |
и т. д. |
|
|
|||
Пример 3.1. |
Пусть |
xn = c постоянная |
последовательность. До- |
|||
казать, что limxn |
= c. |
|
|
|
||
|
|
n |
|
|
|
|
Решение. Пусть выбрано произвольное |
> 0. Нам нужно найти |
|||||
такое число k , |
что при всех n > k выполнялось |
бы неравенство |
||||
| xn c |< . |
Но это неравенство равносильно следующему: | c c |< , |
|||||
или 0 < , |
что выполняется для всех номеров n . Это означает, что в |
|||||
качестве |
k |
можно выбрать любое число, например, |
k = 0 . Тогда для |
|||
любого |
n > k имеет место неравенство | xn |
c |< . |
По определению |
|||
limxn = c .
n
Замечание. В разобранном примере число k удалось выбрать так, чтобы оно годилось сразу для всех . Такой случай не типичен.
|
|
Пример 3.2. Доказать, что lim |
1 |
= 0 . |
|
|
|||||||
|
|
|
|
|
|||||||||
|
|
|
|
n n |
|
|
|
|
|
||||
|
|
Решение. Пусть фиксировано произвольное > 0. Нам нужно найти |
|||||||||||
такое число k , что при всех n > k |
выполнялось бы неравенство |
||||||||||||
| |
1 |
0 |< , или n > 1/ . Выберем k = 1/ |
. Тогда при n > k имеем: |
||||||||||
n |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
0 |
|
= |
|
1 |
< |
1 |
= . |
||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||
|
|
|
n |
|
|
|
n |
k |
|||||
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
13

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
По определению lim |
1 |
= 0 . |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
|
|
n n |
|
|
|
|
|
||||
Вопрос. |
Пусть |
limxn = a , > 0 |
и |
число k |
такое |
что |
|||||
|
|
n |
|
|
|
|
|
||||
xn (a , a ) |
при n > k . |
Можно ли утверждать, что в интервале |
|||||||||
(a ; a ) |
нет ни одного из чисел xn , |
n k ? |
|
|
|||||||
Ответ. Нет. Приведѐм соответствующий пример. Определим |
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
при n чѐтном; |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
xn = n |
|
|
|
|
|
||||
|
|
|
|
|
при n нечѐтном. |
|
|
||||
|
|
|
|
0 |
|
|
|||||
Последовательность |
(xn ) |
имеет предел, |
равный |
нулю. |
Пусть |
||||||
= 0,01, тогда все члены с номерами |
n > 100 попадают в интервал |
||||||||||
( ) , а, например, член x100 = 0,01 уже не попадает в него. Однако члены x1 , x3 , , x99 с нечѐтными номерами тоже лежат в ( ) .
Наглядное представление о пределе можно получить, считая, что xn какие-то физические величины, которые мы можем измерять с
определѐнной точностью, допускаемой приборами. Пусть |
есть |
||
точность прибора, |
тогда неравенство | xn a |< |
означает, что мы не |
|
сможем отличить |
xn от a. Таким образом, |
условие lim xn |
= a |
|
|
n |
|
означает, что при любой точности измерения последовательность (xn ) ,
начиная с некоторого номера, не отличается от постоянной последовательности a , a , a , ... .
Вопрос. Могут ли два разных числа быть пределами одной и той же последовательности?
Ответ. Нет. Предположим, что два разных числа a и b являются пределами одной и той же последовательности (xn ) и пусть, например, b > a . Положим = (b a)/3 , тогда -окрестности точек a и b не пересекаются (сделать чертѐж!). Ввиду условия найдутся такие числа
k1 и k2 , что при всяком n > k1 |
член xn лежит в -окрестности точки |
a и при всяком n > k2 член xn |
лежит в -окрестности точки b . Если |
теперь взять какое-нибудь n > max{k1,k2}, то окажется, что xn лежит
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
14

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
одновременно в -окрестности точки a и в -окрестности точки b , а это невозможно, поскольку окрестности не пересекаются.
Пример 3.3. Доказать, что если | q |< 1, то limqn = 0.
n
Решение. Если q = 0, то qn = 0 при любом n, в этом случае утверждение очевидно.
Для случая q 0 предварительно установим одно вспомогательное
неравенство. |
По условию | q |< 1, |
тогда |
1 |
> 1 и, значит, |
1 |
|
= 1 |
|||
|
|
|
||||||||
|
|
|
|
|
|
| q | |
| q | |
|||
для некоторого > 0 . |
Возводя обе части последнего неравенства в |
|||||||||
степень n , |
получим |
1 |
= (1 |
α)n . |
Поскольку > 0 |
, |
то все |
|||
|
|
|||||||||
|
n |
|||||||||
|
|
|
| q | |
|
|
|
|
|
|
|
слагаемые, которые получаются после раскрытия скобок и приведения подобных членов в (1 )n , являются положительными. Одним из
слагаемых является2 n , |
поэтому справедливо |
1 |
= (1 )n > n |
||||
|
|||||||
n |
|||||||
|
|
|
|
|
|
| q | |
|
и, значит, |
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
| q |n < |
|
. |
(3.3) |
|
|
|
|
n |
||||
С помощью полученного неравенства докажем, что limqn = 0 . |
|||||||
|
|
|
|
|
|
|
n |
Мы должны показать, |
что для любого > 0 существует число k , |
||||||
такое что при всех n > k |
выполняется неравенство | qn 0 |=| q |n < ε . |
||||||
1 |
|
|
|
|
|
|
|
Выберем k = |
|
, тогда при n > k |
|
|
|||
|
|
|
|||||
2 Действительно, (1 )n это произведение n |
сомножителей 1 : |
(1 α)(1 α) |
(1 α) . |
Член получается только в случае, когда из одной скобки мы берем , а из остальных - 1. Поскольку у нас всего n скобок, то после перемножения мы
получим n слагаемых вида 1n 1 , т. е. коэффициент перед равен n .
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
15

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
n > |
1 |
n > |
1 |
|
1 |
< |
|||
|
|
n |
|||||||
|
|
|
|
|
|
||||
и в силу (3.3) | qn 0 |=| q |n < |
1 |
< ε , |
что |
и |
требовалось доказать. |
||||
nα |
|||||||||
|
|
|
|
|
|
|
|
||
Отметим, что в параграфе 4 (пример 4.1) будет дано другое доказательство.
Вопрос. Пусть limxn = a , > 0 . Можно ли утверждать, что найдѐтся |
|||
n |
|
|
|
такое число k , что | x a |< при всех n > k ? |
|||
n |
2 |
|
|
|
|
|
|
Ответ. да. Поскольку limxn |
= a , |
то по определению предела для |
|
n |
|
|
|
любого положительного числа |
, а |
следовательно, и для = / 2 , |
|
найдѐтся число k , такое что | xn |
a |< при всех n > k . |
||
Сформулируем необходимое условие существования предела, доказательство которого приводится в следующем параграфе.
Теорема 3.1. Если последовательность имеет предел, то она ограничена.
Пример 3.4. Доказать, что последовательность xn = n2 не имеет
предела.
Решение. В примере 1.5 было показано, что данная последовательность не является ограниченной. По теореме 3.1 заключаем, что после-
довательность (xn ) расходится.
Следующий пример показывает, что ограниченная последовательность может и не иметь предела, т. е. обратное утверждение к теореме 3.1 неверно.
Пример 3.5. Доказать, что последовательность xn = ( 1)n не имеет
предела.
Решение. Предположим противное, т. е. какое-то число a является
пределом этой последовательности. |
Тогда для = 1 найдѐтся такое |
|||
число |
k , что | xn a |< 1 при всех |
n > k . Пусть номер N > k , тогда |
||
| xN 1 |
a |< 1 и | xN 2 a |< 1. Но одно из чисел xN 1 |
и |
xN 2 равно 1, а |
|
другое равно –1. Поэтому | 1 a |< 1 и |1 a |< 1, |
т. |
е. одновременно |
||
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
16

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
0 < a < 2 и 2 < a < 0 . Полученное противоречие показывает, что последовательность (xn ) расходится.
При вычислении пределов на практике редко пользуются определением. Обычно применяют стандартные предельные равенства (см. примеры 3.2 и 3.3) и следующую теорему об арифметических операциях с пределами.
Теорема 3.2. Если последовательности (xn )
сходятся и |
последовательности |
(xn yn ) , |
||
последнем случае предполагается yn |
0, lim yn |
|||
|
|
|
|
n |
1) |
lim (xn |
yn ) = lim xn |
lim yn ; |
|
|
n |
n |
n |
|
2) |
lim (xn |
yn ) = (lim xn ) (lim yn ) ; |
||
|
n |
n |
n |
|
и ( yn ) сходятся, то
(xn yn ) и xn / yn (в
0 ). При этом
|
xn |
|
lim xn |
|
3) lim |
= |
n |
. |
|
|
|
|||
n yn |
|
lim yn |
||
|
|
|
n |
|
Доказательство теоремы 3.2 обсуждается в следующем параграфе. Пример 3.6. Доказать, что постоянный множитель можно выносить
за знак предела, т. е. lim cxn |
= c lim xn для любого c R . |
n |
n |
Решение. В самом деле, рассмотрим последовательность yn = c .
Поскольку lim yn = c (пример 3.1), то по теореме 3.2 2)
n
lim cxn = lim c lim xn = c lim xn . |
||||||||||
n |
n |
n |
n |
|||||||
Пример 3.7. Показать, что lim |
1 |
= 0 . |
|
|
||||||
|
|
|||||||||
|
|
|
n n2 |
|
|
|
|
|
||
Решение. Поскольку lim |
1 |
|
= 0 , то по теореме 3.2 2) |
|||||||
|
||||||||||
n n |
|
|
|
|
|
|
|
|||
lim |
1 |
= lim |
1 |
lim |
1 |
= 0. |
||||
|
|
|
|
|||||||
n n2 |
n n |
n n |
|
|||||||
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
17

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
Замечание. Теорему 3.2 можно обобщить на произвольное |
||
(конечное) число слагаемых (сомножителей). В частности, lim |
1 |
= 0 |
|
||
n nm |
|
|
для любого m N . |
|
|
Пример 3.8. Найти lim |
(n 2)3 |
n(n 1)2 |
. |
|
n2 |
11 |
|||
n |
|
Решение. Обозначим дробь, стоящую под знаком предела, через xn . В числителе и знаменателе xn стоят последовательности, не
являющиеся ограниченными (доказывается аналогично примеру 1.5). По теореме 3.1 они не имеют предела и теорема о пределе частного (теорема 3.2 3)) «напрямую» здесь неприменима. Поступим следующим образом: поделим числитель и знаменатель на наибольшую степень n .
По формулам сокращѐнного умножения (n 2)3 n(n 1)2= 8n2 11n 8 , так что xn можно переписать в виде:
|
|
|
|
|
11 |
8 |
|
|
|
11 |
8 |
|
|
|||||||
|
8n2 11n 8 |
= |
n2 |
(8 |
|
|
|
|
|
) |
= |
8 |
|
|
|
|
|
|
|
. |
x = |
|
n |
|
n2 |
|
n |
|
n2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
n2 11 |
|
|
n2 (1 |
11 |
) |
|
|
1 |
11 |
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
n2 |
|||||||
Теперь в числителе и знаменателе xn |
стоят сходящиеся последователь- |
|||||||||||||||||||||||||||||||||||||
ности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
8 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||
lim |
|
8 |
|
|
|
|
|
|
= lim 8 11lim |
|
|
|
|
8 lim |
|
|
= 8, |
|||||||||||||||||||||
|
|
n2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
n |
|
|
|
n |
|
|
|
|
|
n |
|
n n |
|
|
|
|
|
|
|
|
n n2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
11 |
|
= lim1 11lim |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
lim |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
= 1. |
|
|
|
|
|
|||||||||||||||||
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
n |
|
|
|
|
n |
|
n n2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
По теореме 3.2 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
11 |
|
|
|
8 |
|
|
|
|
|
11 |
|
|
8 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
8 |
|
|
|
|
lim 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
2 |
|
|
|
8 |
|
||||||||||||||||||
|
|
|
|
|
n |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
lim xn |
= lim |
|
|
|
|
|
|
= |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
= 8. |
||||||||||||||
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
1 |
||||||||||||||
n |
|
n |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ. 8.
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
18

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
Определение. Геометрическая прогрессия (xn ) называется бесконечно убывающей, если | q |< 1, где q знаменатель прогрессии. Суммой бесконечно убывающей геометрической прогрессии называется
число S = lim Sn , где Sn сумма еѐ первых n членов.
n
Пример 3.9. Доказать, что если геометрическая прогрессия (xn ) с показателем q является бесконечно убывающей, то еѐ сумма равна
x1 .
1 q
|
|
|
|
|
|
|
|
|
|
|
qn |
1 |
|
|
|
|
x |
|
qn |
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||
Решение. Так как S |
|
|
= x |
|
|
|
|
|
|
|
= |
|
1 |
|
|
|
|
1 |
|
, то |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
1 q 1 |
|
|
|
q 1 |
1 |
q |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
S = lim Sn |
= |
|
|
|
x1 |
|
lim qn lim |
|
|
|
x1 |
|
= |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
q |
|
1 q |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
1 n |
|
|
|
|
n |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
x1 |
|
0 |
|
x1 |
|
= |
|
|
x1 |
. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
q 1 |
|
q |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Пример 3.10. Записать значение |
выражения 1,7(5) = 1,7555 в |
||||||||||||||||||||||||||||||||||||||||||||
виде обыкновенной дроби. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение. Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
7 |
|
|
5 |
|
|
5 |
|
|
5 |
|
|
|
17 |
|
|
|
|
|
|
|
|
17 |
|
|
1 |
|
79 |
|
||||||||||||||||
1,7(5) = 1 |
|
|
|
|
|
|
= |
|
102 |
|
|
= |
|
= |
. |
||||||||||||||||||||||||||||||
|
102 |
103 |
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
10 |
|
|
|
|
104 |
|
|
|
|
|
|
10 |
|
|
10 |
|
18 |
|
45 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
||||||||||||
Ответ. 79/45.
Следующее полезное свойство пределов известно под названием
теоремы о «зажатой» последовательности.
Теорема 3.3. Пусть (xn ), ( yn ) и (zn ) такие последовательности,
что xn yn |
zn при всех n N и limxn |
= limzn |
= a . Тогда limyn = a . |
|
n |
n |
n |
Доказательство. Для данного > 0 существует такое число k1 , что
члены xn |
лежат |
в интервале |
(a , a ) |
при всех |
n > k1 , и |
существует |
такое число k2 , |
что члены zn |
лежат в |
интервале |
|
(a a ) |
при |
всех n > k2 . |
Положим k = max{k1 ,k2 } . |
Тогда при |
|
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
19

2013-2014 уч. год, №3, 10 кл. Математика. Последовательности. Пределы
n > k одновременно |
|
xn (a a ) |
|
|
и |
zn (a a ) и, |
|||||||||||||
следовательно, a < xn |
yn |
zn |
< a , |
т. е. |
yn (a a ) , что |
||||||||||||||
и требовалось. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3.11. Дана последовательность |
|
|
|
|
|
|
|
||||||||||||
xn |
= |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n2 |
|
|
n2 |
|
2 |
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
n2 n |
||||||||||
Доказать, что lim xn |
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Попробуем «зажать» |
xn между членами последователь- |
||||||||||||||||||
ностей, сходящихся к одному и тому же числу, и применим теорему
3.3.
Заметим, что |
|
1 |
|
наибольшая, а |
|
1 |
|
наименьшая дробь |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
n2 |
1 |
n2 n |
|
|
||
суммы xn . Тогда верна оценка n |
|
|
1 |
|
|
xn n |
1 |
|
|
. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
n2 n |
|
n2 |
1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Поскольку n2 n < n2 2n 1, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
n |
. |
||||
|
n2 n < n 1 |
|
|
|
|
> |
|
|
|
|
> |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
n2 n |
|
|
n |
1 |
|
|
n2 n |
|
|
n 1 |
||||||||
Учитывая |
|
n |
|
< |
n |
= 1 , получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
n2 1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Поскольку
limxn = 1 .
n
|
|
n |
< |
|
|
|
n |
|
|
|
|
|
xn |
|
|
n |
< 1. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
n2 |
n |
n2 1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
lim |
|
n |
= lim |
|
|
|
1 |
|
|
|
|
= 1 |
и |
lim1 = 1, по теореме 3.4 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
|
||||||||||||||
n n 1 |
|
n |
|
|
|
|
|
|
|
n |
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||
§4*. Теоремы о пределах
Этот параграф посвящѐн доказательству основных теорем теории пределов. Формулировки некоторых из них были приведены в параграфе 3.
2013, ЗФТШ МФТИ, Редкозубова Елена Юрьевна
20
