§3 П. 14, 15 № 2, 3(1) с.34

Лекційно-практичне заняття 2

Перпендикулярність прямих і площин в просторі

Тема. Побудова прямої та площини, перпендикулярних між собою. Властивості прямої та площини, перпендикулярних між собою.

План

1. Побудова прямої і площини, перпендикулярних між собою.

2. Властивості прямої і площини, перпендикулярних між собою.

3. Розв’язання вправ.

Література.

1. Погорєлов О.В. Геометрія. Стереометрія. Підручник за 10-11 кл. Київ : Освіта, 1994 – 128с.

2. Афанасьєва О.М., Бродский Я.С., Павлов О.Л. Геометрія 10 -11кл. : Пробний підручник. – Тернопіль: Навчальна книга – Богдан, 2004

Перебіг заняття

1. Побудова прямої і площини, перпендикулярних між собою.

Розв’язання вправ:

1) Дано пряму а і точку А поза нею. Проведіть через точку А площину перпендикулярну до прямої а.

2) Дано пряму а і точку А на ній. Проведіть площину, яка проходить через точку А і перпендикулярна до прямої а.

3) Скільки площин, перпендикулярних до даної прямої, можна провести через дану точку? Доведіть це.

4) Дано площину і точку А поза нею. Проведіть через точку А пряму, яка б була перпендикулярна до площини .

5) Дано площину і точку А на ній. Проведіть через точку А пряму, яка б була перпендикулярна до площини .

6) Скільки прямих, перпендикулярних до даної площини, можна провести через дану точку простору? Доведіть свою думку.

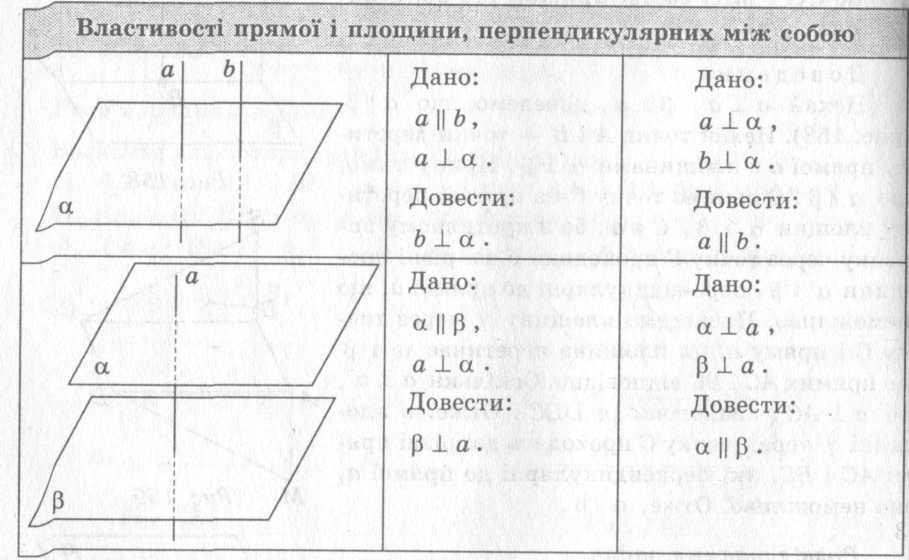
2. Властивості прямої і площини, перпендикулярність між собою

Теорема 3. Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона і перпендикулярна й до другої (рис.3).

Рис. 3

Доведення

Нехай . Доведемо, що. Точки А₁ та А₂ – точки перетину а₁ та а₂ з площиною . У площинічерез точку А₂ проведемо довільну пряму х₂ , а через А₁ - пряму х₁ таку, що . Оскільки, то за теоремою 3.1.. Оскільких₂ вибрана довільно в площині , то.

Теорема 4. Дві прямі, перпендикулярні до однієї і тієї самої площини, паралельні (рис.4).

Рис.4

Теорема 5. Якщо пряма перпендикулярна до однієї з двох паралельних площин, то вона перпендикулярна до другої.

Теорема 6. Якщо дві площини перпендикулярні до однієї і тієї самої прямої, то вони паралельні.

3. Закріплення та осмислення вивченого матеріалу

1) Робота зі схемою.

• Як розташовані прямі, які перпендикулярні до площини?

• Як розташовані в просторі площини, які перпендикулярні до прямої?

• Як розташовані пряма і площина, якщо паралельна пряма до даної прямої перпендикулярна до площини?

• Як розташовані пряма і площина, якщо площина, паралельна до даної площини, перпендикулярна до даної прямої?

2) Задача №7 (підручник с. 34).

Відповідь: 2 м.

3) Задача №8 (підручник с. 35).

4) Задача №16 (підручник с. 35).

Відповідь: 9 м .

Контрольні запитання

• Які прямі в просторі називаються перпендикулярними?

• Які властивості прямої і площини, перпендикулярних між собою, ви знаєте?

• Сформулюйте ознаку перпендикулярності прямої та площини.

• Скільки прямих, перпендикулярних до даної площини, можна провести через дану точку?

• Скільки площин, перпендикулярних до даної прямої, можна провести через дану точку?

Домашнє завдання