Лекція 1

Перпендикулярність прямих і площин в просторі

Тема. Перпендикулярність прямих. Перпендикулярність площини і прямої. Ознаки перпендикулярності прямої та площини.

План

1. Перпендикулярність прямих у просторі.

2. Означення перпендикулярності прямої і площини.

3. Ознака перпендикулярності прямої і площини.

Література

1. Погорєлов О.В. Геометрія. Стереометрія. Підручник за 10-11 кл. Київ : Освіта, 1994 – 128с.

2. Афанасьєва О.М., Бродский Я.С., Павлов О.Л. Геометрія 10 -11кл. : Пробний підручник. – Тернопіль: Навчальна книга – Богдан, 2004

Перебіг заняття

1. Перпендикулярність прямих у просторі

Означення. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом перпендикулярним прямим, то вони теж перпендикулярні (рис.1).

Рис. 1 Рис. 2

2. Означення перпендикулярності прямої і площини

Уявлення про пряму перпендикулярну до площини дають вертика­льно поставлені стовпи — вони перпендикулярні до поверхні землі, пер­пендикулярні до будь-якої прямої, яка проходить через основу стовпа і лежить у площині землі.

Означення. Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину та перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину.

На рис. 3 пряма с перпендикулярна до площини . Пишуть:с . З означення випливає, що с а , с.

Рис. 3

3. Ознака перпендикулярності прямої та площини

Теорема 2. Якщо пряма перпендикулярна до двох прямих, які лежать у площині і перетинаються, то вона перпендикулярна до даної площини.

а

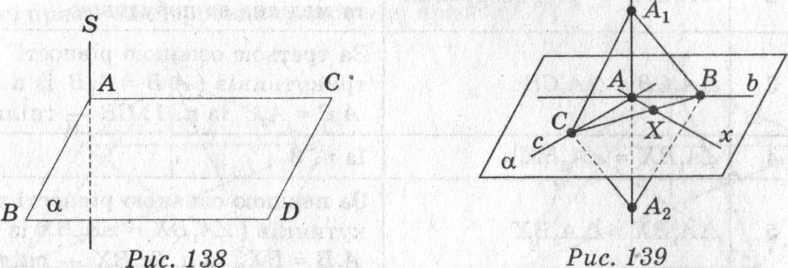
Дано: а с , а, ,; перетинаються в точці А; ,х – довільна пряма.

Довести: а х.

Доведення

Додаткові побудови: проводимо пряму в площині , яка перетинає пряміb, х, с в точках B, X,С, та відкладаємо на прямій а АА₁ = АА₂.

№ п/п	Твердження	Аргументи
1	—рівнобедрений	АС — висота за умовою та медіана за побудовою
2	А1ВА2 - рівнобедрений	АВ — висота за умовою та медіана за побудовою
3	А1СВ = А2СВ	За третьою ознакою рівності трикутників (А1В - А2В із п. 2; А1С = А2С із п. 1; СB — спільна)
4	A1ВХ = 2ВХ	Із п. 3
5	А1ВХ = А2ВХ	За першою ознакою рівності три­кутників ( A1ВХ = 2ВХ iз п. 4; А1В = ВА2 із п. 3; ВХ — спільна)
6	А1Х = А2Х	Із п. 5
7	А1ХА2 — рівнобедрений	А1Х = А2Х
8	ХА — медіана є висотою: ХА А1А2	А1ХА2 — рівнобедрений

Теорему доведено.

4. Закріплення та осмислення вивченого матеріалу

1) SABC – тетраедр,. ТочкиK, L, M – середини ребер SB, SA, SC відповідно ( рис.2). Знайти .

2) Ребро куба дорівнює а. Знайдіть довжину діагоналі грані куба. (Відповідь: ).

3) Укажіть в оточуючому просторі моделі прямих і площин, які перпендикулярні.

4) Чи правильне твердження: коли пряма не перпендикулярна до площини, то вона не перпендикулярна ні до жодної прямої, яка лежить в цій площині? (Так)

5) Пряма SA перпендикулярна до площини прямокутника ABCD. Укажіть перпендикулярні прямі.

6) Через точку О перетину діагоналей квадрата зі стороною а проведено пряму ОК, перпендикулярну до площини квадрата. Знайдіть відстань від тоски К до вершин квадрата, якщо ОК=b. (Відповідь: ).

7) Ребро куба дорівнює а. Знайдіть відстань від точки перетину діагоналей однієї із граней до вершин протилежної їй грані. (Відповідь: ).

8) Діагональ BD₁ прямокутного паралелепіпеда дорівнює d, діагональ AD₁ грані дорівнює b. Знайдіть АВ. (Відповідь: ).

9) Задача №5 (підручник с.34).

Контрольні запитання

• Які прямі в просторі називаються перпендикулярними?

• Чи визначають площину дві перпендикулярні прямі? Чому?

• Сформулюйте теорему про прямі, які перетинаються і відповідно паралельні перпендикулярним прямим.

• Сформулюйте ознаку перпендикулярності прямої та площини.

Домашнє завдання