M2 - 1.Понятие функции. Функции действительного переменного. Способы задания функции. Свойства функций.

Опр. Пусть заданы мн-ва E и F, если xE по определённому закону (правилу) f ставится в соответствие некоторый единственный элемент yF, то говорят, на E задана ф-я f со значениями в F или отображение f мн-ва E во мн-во F.

В этом случае E – область определения ф-и, символ x– аргумент ф-и или независимая переменная.

Пусть x₀E – конкретное значение аргумента x, соответствующий этому значе­нию аргумента элемент y₀F называют значением ф-и на элементе x₀ или значением ф-и при значении аргумента x=x₀ или образом элемента x₀ при отображении f и обозначают f(x₀). При изменении аргумента значения y=f(x) F вообще говоря меняются в зависимости от x. По этой причине величину y=f(x) часто называют зависимой переменной.

Мн-во всех значений ф-и, которые она принимает на элементах мн-ва E, называют мн-вом значений или областью значений ф-и. Иногда, f(E) называют образом мн-ва E при отображении E в F.

Если элементы E и F являются вещественными числами, то говорят о ф-ции действительного или вещественного переменного.

Для ф-ции принимают следующие обозначения: или .

Н-р: А-мн-во нат.чисел. ,-отображение. -отобр-ие.

Виды отобр-ий.

Опр Говорят что отобр f мн. Е в F является инъективным или обратимым, если 2 различных элемента из Е имеют образами при отображении f два различных элем. в F.

() () или: если .

Пример: f(x)=2x задано на мн-ве Z - инъект, т.к. если ,

Опр. f: EF наз. сюрьективным, если любой элем мн-ва F имеет прообраз при этом отобр. ().

Пример: Отобр. f(x)=2x задано на мн-ве Z . не сюрьективно, т. к. напр. Ур-ие 3= 2x не имеет решения на мн-ве Z.

y= -сюрьективно, но не иньективно.

Опр. Пусть f есть отобр. Е на F. Если любой эл-т yF явл. при отобр. f образом единственного эл-та xE то отобр. f наз. взаимно однозначным или биективным. (т.е, если отобр. яв-ся инъект и сюръект).

Пример: y=2-биекция из R во мн-во неотр. действ чисел, т. к. x ! положит знач y, при кот-ом y=2 и полож y ! знач x, при кот-ом y=2, а именно x=logy.

Опр: Пусть наз-ся действит.ф-ией д-го аргум-та.

Н-р:

Способы задания функции:

1. Аналитический.

1.1Ф-я задается с помощью формул, т. е. аналитического выражения.

Пример: y=x+1

Под ф-цией, заданной некоторой формулой понимается ф-ция, определенная на мн-ве всех тех вещественных чисел, для которых:

1) указанная формула имеет смысл;

2) в ходе проведения всех необходимых вычислений получаются только вещественные числа, в случае ф-ции действительного переменного.

Опр:Естественной обл.опр.ф-ии, заданной аналитич.выраж-м, наз-ся мн-во всех тех и только тех знач.арг-та, д/кот.вып-ся весь комплекс операций, участвующий в задании ф-ий.

1.2параметрическое задание

Рассмотрим системы ф-ций:

(1). Предположим, что ур-е разрешимо относительно переменной t, т.е. 1 –е уравнение имеет обратную ф-цию , подставив во второе ур-е, получим (2), где xE(φ), тем самым мы показали, что система задает некоторую ф-цию y=f(x). Переход от задания ф-ции в виде (1) к заданию ф-ции в виде (2) называют исключением параметра t. Обратный переход от (2) к (1) называют параметризацией ф-ции.

Пример:

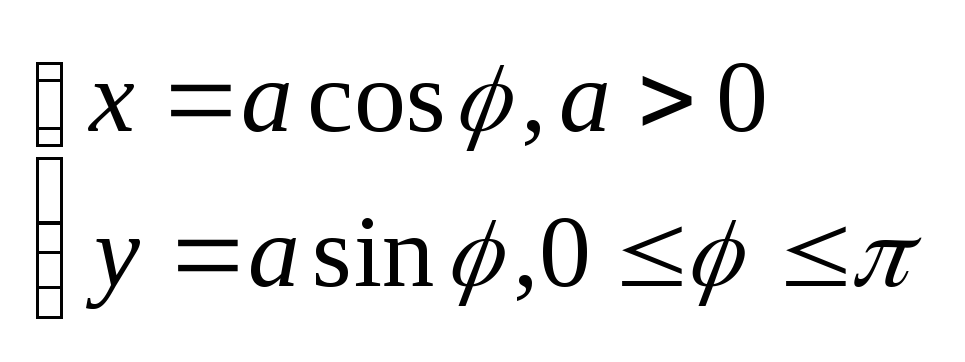
1.3 Неявно заданные функции.

Рассм. ур-ие F(x,y)=0 (1)

Рассм. мн-во X т. ч. xXхотя бы одно число y, т. ч. F(x,y)=0. Выберем одно из этих чисел и обозн. ч-з .Тем самым по средствам ур-ия (1) на мн-ве X задана ф-ия, обозн y=f(x). Мы имеем по усл. F().

Ф-ии, неявно заданные ур-ем (1) наз. неявными функциями.

Пример: y-x-1=0.

Термин неявной ф-ии отражает не характер функц-ной зависимости, а лишь способ ее задания. Одна и та же ф-ция м. б. задана как явно, так и неявно.Пр: y=x-1(явно), y-x+1=0 (неявно)

Недостатки: для нахождения знач ф-ии каждый раз необх проводить вычисления

2.Графический.

На пл-ти рассм-м систему координат и зададим кривую Г, соотв-ую пром-ку (a,b) и удовл. след-му усл-ию: любая прямая, пар-ая оси oy и прох-ая ч-з пром-к (a,b) пересекает Г только в одной точке. Такая кривая наз-ся графиком.

Опр. Графиком ф-ии y=f(x) наз-ся мн-во точек на пл-ти с коор-ми (x,f(x)), где x E.

Недостатки: неточность

3.Табличный(табл синусов, логарифмов, квадратов, кубов, таблица Брадиса)

Недостатки: можно найти значение функции лишь в точках, определенных в таблице.

4.Описательный (словесный). Всякая формула является лишь записью некоторого где–то описанного ранее соответствия, так что, в конце концов, нет принципиального различая между заданием функции с помощью формулы или описанного соответствия.

Пример: Напр. D(x)= -функция Дирихле. График этой ф-ии нельзя построить, т.к. эта ф-ия разрывается в каждой точке D(f) и не интегрируема по Риману. Функция имеет период – любое рац число, но не имеет наименьшего периода.

Недостатки: редко используется.

5.С помощью диаграмм.

Свойства функций

Опр. Ф-ция f на промежутке E является возрастающей (убывающей) если , (для убывающей ). Если между значениями функций стоит знак нестрогого неравенства, то функция является неубывающей (невозрастающей).

Пример. Доказать, что функция f(x)=1-х является убывающей на всем множестве R. Пусть x₁<x₂ и x₁, x₂ R произвольные, тогда f(x₂)-f(x₁)=1-x₂-1+x₁; f(x₂)-f(x₁)= x₁-x₂; т.к. x₁<x₂, то x₁-x₂<0, значит f(x₂)-f(x₁)<0; т.е. f(x₁)>f(x₂), следовательно, по определению, функция f(x)=1-x убывает, а в силу произвольности x₂ и x₁ функция убывает на всем множестве R.

Опр. Функция, которая является либо невозрастающей, либо неубывающей называется монотонной. Если выполняется знак строгого неравенства, то функция строго монотонна.

Опр. Ф-ия f:Eназ-ся ограниченной на Е, е/и М>0, т.ч. |f(x)|<=M.

Пример: показательная функция.

Опр. Говорят, что ф-ция f на E является четной (нечетной), если: 1) множество E симметрично относительно 0; 2) f(-x)=f(x), , (f(-x)=-f(x)), xE.

Сумма 2-х чет (нечет) ф-ий есть ф-ия чет (нечет); сумма чет и нечет ф-ий есть ф-ия общ вида; произвед двух чет (нечет) ф-ий есть чет ф-ия; произвед чет и нечет ф-ий есть ф-ия нечет.

Опр. Ф-ция f называется периодической, если такое, что , где T –период ф-ции.

Опр. Пусть f:Xяв-ся сюр-ой. Возьмем y. Т.к ф-ия сюр-на, то сущ-ет х, т.ч. f(х)=y. Т.о. будет определено правило, сопост-ее yx. е/и это правило яв-ся ф-ей, то его наз-ют обратной ф-ей, а саму ф-ию обратимой.

Пример: f(x)=2x-1,

x=(f(x)+1)/2, F(x)=(x+1)/2 – ф-ия, обратная f(x).

Опр. Ф-ия f(x) наз-ся непрерывной в точке а, е/и

1) f определена в нек-ой окр-ти точки а и конечно в самой точке а

2) сущ-ет конеч. Предел

3)

Опр. Композицией ф-ий f и g называется ф-ия, определяемая рав-вом g○f(x)=g(f(x)) для всех х, для кот первая часть рав-ва имеет смысл.

Пример: y=x², z=2y+1, D(x)=R, D(y)=R, E(x)=[0; бескон), Е(у)=R.

Z(y(x))=2x²+1.

M2 - 2. Пон-е производной.

Диф-ть ф-ции. Диф-ал. Правила диф-ния. Диф-ние осн-х эл-ов ф-ций.

Опр4. Касательной к графику ф-ии f(x) в точке M₀ называется прямая M₀Т, прох-ая ч/з т. M₀(x₀;f(x₀)) и облад.тем св-ом, что (-угол м/у секущей M₀М и прямой M₀Т.

Уравнение касательной в точке с абсциссой x=x₀, где x₀графику ф-ии f y=f(x₀)+f ^/(x₀)(x- x₀)

Задача о кас-ой.

Пусть в т. M₀(x₀;f(x₀)) имеет касательную. Поставим з-чу: найти угл.коэф-т кас-ой в т. x_0.

д/ получ.угл.коэф-та касат.нужно перейти к пределу при ∆x→0

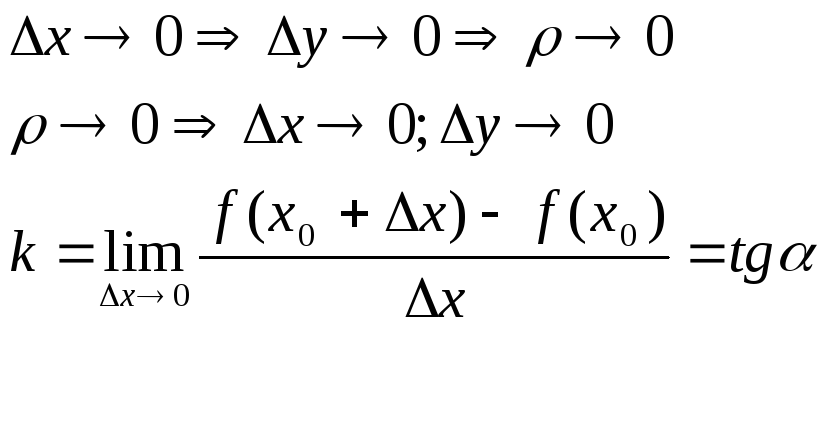
З-ча о мгнов.скорости

S=f(t)

Поставим задачу: найти v мгновенную в момент времени t_0.

зафиксируем от начала движ-ия

-путь от

Дадим времени приращение

Тгда

Опр. Производной от ф-ии f в т. наз-ся предел (е/и он сущ) отношения приращения ф-ии в т. к соотв-му приращ-ию аргумента, когда поледнее стремится к нулю.

Н-р:

Опр. Пусть д/ y=f(x) ; D(f)в каж. т. мн-ва сущ.производная, тогда каж. поставим в соотв-ие зн-е произв-ой в этой т.Такое соотв-ие функц-но; на мн-ве D оно задает ф-ию f’ , кот.наз-ся производной ф-ией от ф-ии f.

Опр. Ф-ия y=f(x) наз-ся дифференц-ой в т. , е/и приращение ф-ии в этой т.м.б.представлено в виде:

отн-но ;

Н-р:

Ф-ия дифф-ма в любой т.из R

Опр: Пусть ф-ция у=f(х) диф-ма в (.)-ке x₀. Главая часть приращ-я ф-ции – линейна относ-но Δx, наз-ся диф-лом ф-ции в (.)-ке x₀ и обознач-ся

Теорема: Е/и ф-ия y=f(x) дифф-ма в т. , то она имеет в этой т. произ-ую, причем произв-ая в представлении приращения

Док-во:

Пусть у=f(х) диф-ма в (.)-ке x₀, это значит, что её приращ-е

отн-но ;

Е/и сущ., то

Опр. По опр.дифф-ал независ.переменной есть . Е/и в опр.дифф-ал заменить на , то получим -это инвариантная форма дифф-ла.

Правила дифф-ия.

Т1:Пусть ф-ии f и g имеют производную в точке x₀ – внутр D(f), D(g). Тогда сумма, произведение, частное этих ф-ций также имеет производную в точке x₀, причем:

1. (f+g)’(x₀)=f’(x₀)+g(x₀)

2. (fg)(x₀)=f(x₀)g’(x₀)+f’(x₀)g(x₀)

3.

Док-во:x₀- внутр. D(f) и D(g) |→ D(f)∩D(g)=D(f+g); (f+g)’(x₀)<по опр>=

След1. Пусть x₀-внутр (.) D(f). f имеет произв-ю в (.)x₀, тогда ф-ия сf, где c=const имеет произв-ю в (.)x₀ причем (cf)’(x₀)=c(f)’(x₀)

След2. x₀ – внутр (.)D(f₁), D(f₂)… D(f_n) и f₁, f₂…f_n имеют произ-е в (.)x₀. Тогда f= f₁∙f₂…f_n т/же имеет произв-ю в (.)x₀

След3.

Дифф-ие элемент-ых ф-ий

1. (sin x)^’= cos x 2. (cos x)^/=-sin x

3.

Док-во:

4. (ctg x)^/= 5. (a^x)^/=a^xln a

6. (e^x)^/=e^x

7.

8. (ln x)^/=1/х

9.

10.

11.

12.

М2-3.Основные теоремы дифференциального исчисления, их приложения к исследованию функций.

Т. Ферма. Пусть ф-ция f определена и непрер-вна на (a, b) и в т.C этого интервала достигает наиб. или наим. значение этой ф-ции на интервале (a, b) в т.C . Если производная f ’(c) существует, то .

Т. Роля. Пусть ф-ция f: 1) определена и непрерывна на [a,b];

2) имеет в каждой точке интервала (a,b) производную;

3) на концах отрезка принимает равные значения: f(a)=f(b).

Тогда существует т.C є (a,b) такая, что

Т. Лагранжа.

Пусть ф-ция f: 1) определена и непрерывна на [a,b];

2) имеет в каждой точке интервала (a,b) производную;

Тогда сущ-ет такая т.C є (a,b), что справедливо равенство:

Док-во: Рассмотрим вспомогат. ф-цию F(x)=f(x)- f(а)- .

Для F(x) выпол.след.усл.1). F(x)-непрерывна и определена на [a;b]; 2). F’(x)= f’(x)-.существует в (a,b);3). F(а)=0; F(b)= f(b)- f(а)- *(b-a)=0.Все условия Т.Ролля вып-ся, следовательно , что F’(с)=0,Значит, f’(с)= .

Теорема Коши.Пусть ф-ции f и g:1) определены и непрерывны на [a,b];2) f’ и g’ сущ-ут хотя бы в (a,b),причем Тогда существует такая т.Cє (a,b), что справедлива формула:

Приложения: Условие постоянства функции

Т1:Е\и непрерывная на отрезке[a,b] функция f имеет хотя бы в (a,b) производную =0, то функция f- постояннана этом отрезке.

Условие монотонности функций.

Т2:для того чтобы функция f непрерывная на [a,b] и меющая производную хотя бы в (a,b) была возрастающей (убывающей) на [a,b] необх и достат чтобы 1) f’(x) на (a,b) была положительной (отрицательной); 2) f’(x)=0 выпол-сь только в отдельных точках (a,b).

Док-во: «необх»пусть для определ-ти f(x) сторого возрастает на [a,b] зададим произвол-е х из [a,b].Дадим ему прирщение Δх, что х+Δх є[a,b].Рассм-м разность f(х+Δх)-f(x), она >0 е\и Δх>0 и <0 е\и Δх<0, тогда отношение >0 будет иметь четко опред-ный знак.,т.е. f’(x)0 на(a,b). Покажем,что рав-во f’(x)=0 не выпол. ни в каком промеж-ке (a,b) .МОП f’(x)=0 на нек. (α,β) є(a,b), тогда f(x)-постоянна на нем,что против-чит усл.возрастания.

«дост»пусть f’(x)0 на (a,b) и f’(x)=0 не выпол.ни в каких промеж-ках в (a,b).Возьмем два произ-ных знач-я x₁<x₂ из[a,b],т.к. f-непрер. и имеет производную,то она обл. теми же св0ми и на(x₁,x₂) є[a,b].Применим т.Логража f(x₂)-f(x₁)=f’(c)*(x₂-x₁),где x₁<c<x₂,т.к. f’(x)0, то f’(с)0,тогда f(x₂)-f(x₁)0,т.е. f(x₂) f(x₁).Покажем,что знак рав-ва в данном случае невозможен.МОП предпол.f(x₁)=f(x₂),тогда для любого х є[x₁,x₂] f(x₁) f(x) f(x₂),учит. что f(x₁)=f(x₂) и f-постоянна,что противоречит условию.ЧТД.

Пр:f(x)=x+cosx. D(f)=R,f’(x)=1-sinx, для лбюбого x из D(f) f’(x)0.f’(x)=0 x=+2πk,т.е. f’(x)=0 не выпол. на R, а только в дискретных точках.Функция f(x) возр-ет.

Точки экстремума.

О1:Точка x₀є D(f) назыв. т. нестрогого минимума(нестр. максимума),е\и сущ-ет окрестность U(x₀) т. x₀, что для любого x є U(x₀) выполняется нер-во: f(x₀) f(x) (f(x₀)f(x))

О2:точка x₀є D(f) назыв. т. Строгого минимума(строгого максимума)е\и сущ-ет проколотая окрестность т.x₀,что для любого x из этой окрестности выполн. f(x₀)<f(x)(f(x₀)>f(x)).

Максимум и минимум функции называется экстремумом.

Пр:

Необх.усл.экстремума:Т:е\и в т.х₀ фун-я f имеет экстремум,то либо f’(x₀)=0,либо f’(x₀)- не сущ-ет.

1 дост усл-е экстремама:Т:пусть фун-я f диф-ма в некот.окр-ти(х₀-δ,х₀+δ) критич.т.х₀ за исключ. М.б. самой т.х₀ в котор.f-непрер. и ее производная сохраняет знак.Е\и при переходе ч\з т.х₀ слева на право f’(x) меняет знак,то т.х₀-т.экстремума,причем е\и знак производной меняется с + на - , то max , а с - на +, то min.

Первое правило нахождения экстремума

1. Находят область определения.

2.Найти критические точки ф-ции.

3.Исследовать поведение производных в окрест. крит.точек.

2 дост усл-е экст-ма:Т: Если в критич. точке ф-я f дважды дифференцируема и вторая производная в этой точке отлична от нуля, то ф-я имеет экстремум. А именно max, если втор. производная <0 и min, если вторая произв.>0.

Второе правило нахождения экстремума

1. Находят область определения

2. Найти стационарные точки

3.Найти значение второй производной в стационар. точках.

О:График ф-и f-диф-мой в т.х₀ назыв. выпуклым вверх(вниз),е\и сущ-ет такая окрестность т. х₀,что во всех т.этой ф-и график ф-и расположен ниже(выше) касательной к графику,провед. в т.(х₀,f(х₀)).

О:точка х₀ назыв. т. перегиба графика ф-и f,е\и при переходе ч\з т.х₀ график меняет неправление выпуклости.

Т:е\и ф-я f им. непрер. вторую производную в т. х₀ и f”(x₀)>0(f”(x₀)<0), то график ф-и в т. х₀ явл.выпуклым вверх(вниз).

Т:е\и х₀-т.перегиба графика ф-и f,то в этой т. либо f’’(x₀)=0,либо f’’(x₀) не сущ-ет.

Т:пусть ф-я f дважды диф-ма в некот. окрестности т.х₀ за искл. м.б.самой этой точки,тогда е\и при переходе ч\з т.х₀ вторая производная меняет знак, то т.х₀-т.перегиба.

М2-4. Первообразная и неопределенный интеграл. Основные методы интегрирования.

О: Ф-я F наз. первообразной функцией для ф-и f на промежутке <a,b> е\и для любого х<a,b> справедливо рав-во: F(x) = f(x).

Т: (общ вид первообразной). Е\и в некотором промежутке <a,b> ф-я F есть первообразная для f , то и ф-я F+C, где C – const, также будет первообразной для f.

Док-во:

Дано F – первообразная для f на <a,b>, что по опр-ю означает x<a,b> F(x) = f(x). Далее x<a,b> (F(x)+C)=F(x)+C=f(x)+0=f(x), что по опр-ю означает, что F+C – первообразная■

Т: если функции F1 и F2 две первообразные для функции f на (a,b),то они могут отличаться лишь на постоянную.

Док: (F1(x)-F2(x))’=F1’(x)-F2’(x)=f(x)-f(x)=0 для всех х из (a,b). Тогда ф-я F(x)=F1(x)-F2(x) м. б. только постоянной, т.к. ее проихводная на (a,b)=0 (по теореме о признаке постоянства функции).

О. Совокупность всех первообразных ф-й для f определенных на некотором промежутке <α,β> назыв. неопределенным интегралом от ф-ции f на этом промежутке <α,β> и обозн. символом .

В этом обозначении символ  наз. знаком интеграла, f(x)dx наз. подынтегральным выражением, f(x)наз. подынтегральной функцией.

Опр. Операцию нахождения первообразной или неопределенного интеграла от f наз. интегрированием ф-ции f.

Осн. Св-ва неопр-ного интеграла:

1. и

2.

3.Если 0 f(x)dx=f(x)dx

4.Если на <a,b>  f(x)dx и на <a,b>  g(x)dx, то на <a,b>  f(x)+g(x)dx= f(x)dx +g(x)dx.

Интегр-е подстановкой

Т:Е\и ф-я F(x) есть первообразная для ф-и f(x) на J,ф-я х=φ(t) диф-ма ф-я на пром-ке T,имеющая значения в J ,тогда ф-я F(φ(t)) есть первообразная для ф-и f(φ(t))*φ’(t) и имеет место рав-во

Док-во:ф-я F(x)-первообр. f(x) на J,значит след-но dF(x)=f(x)dx.Положим х=φ(t),где tT: dF(φ(t))=f(φ(t)) ;

F(x)+c=;

.ЧТД

Пр:=(lnx=t,=dt)===

Интегрирование по частям

Пусть u,v-есть 2 диф-мые функции. Найдем диф-ал от их произведения:

duv=udv+vdu

udv=duv-vdu

∫udv=∫duv-∫vdu

∫udv=uv-∫vdu – ф-ла интегрир-я по частям

Пр:

М2-5.Определенный интеграл.Ф-ла Ньютона лейбница.Св-ва опр.интеграла и их приложения.

1.з-чи привод. к понятию опред.интеграла.

Площадь кривол.трапеции:

Пусть f- непрерыв., неотриц.1)рассм-им произвол.разбиение отрезка Т точками: a=x₀<…<x_i<x_i+1<..x_n=b

2)ч\з них провед. Прямые ||Oy.В рез-те трапеция разобьется на n-элементарных кривол.трапеций. 3) На каждом отрезке выберем произв. т._i[x_i,x_i+1 и проведем прямую ||Oy. Кривол. Трапеция заменится ступенчатой фигурой. 4)Вычислим S=f(_i)( x_i+1-x_i)=f(_i)x_i и обозн. ч\з =maxx_i. 5)Выведем площадь кривол.трапеции

S=

Работа переменной силы.

Пусть на материал.точку действ. Сила f(x).1)рассм-м разбиение a=x₀<…<x_i<x_i+1<..x_n=b

2) выберем произв. т._i[x_i,x_i+1 и на этом отрезке действует сила F(_i).3)вычисл.работу на i-ом отрезке А_i=F(_i)Δx_i,тогда на всех отрезках А=F(_i)x_i.Значит А=,где

-диметр разбиения.